| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Buga.
Forumaš(ica)
Pridružen/a: 20. 02. 2008. (22:04:58)
Postovi: (18E)16
Spol: 
|
 Postano: 15:37 uto, 11. 1. 2011 Naslov: |
    |
|
|
[quote="Anonymous"][quote="lucky"].... neznam da li ti ideš na predavanja i vježbe s ciljem da nešto naučiš ili samo zato što su obavezna i zato što moraš predat zadaće ???? ... ili pak ideš da vodiš brigu i statistiku tko je koliko puta izostao i tko je kad zadaću predao...
...i ja sam od onih koji su predavali svoje zadaće na vrijeme, a za ostale šta me briga...ja sam svoje obavila, a drugima ako nemogu pomoć neću im ni odmoć time da ih, kao ti, 'blatim' na forumu...kojeg profesor redovito posjećuje....[/quote]
Naravno da idem da naucim nije to upitno u ovom slucaju. Ne znam imas li razloga za takav ton. (osim ako ti ne spadas u tu kategoriju)
Ali i dalje stojim iza toga da bi pravila trebala bit za sve ista zar ne ? Nepravda uvijek boli pa koliko god ona bila. Na kraju svake zadace lijepo pise krajnji rok za predaju iste.
Ne vodim statistiku samo poznam vecinu ljudi i imam dobro zapazanje.
Ne blatim nikog po imenu i prezimenu. Kao to je neki tabu pa se o tom ne smije pricat ili sto?[/quote]
Kaj tebe točno muči? tj. zakaj te to muči?
Da li to na bilo koji način utječe na tvoju ocjenu, znanje, ... ? (osim kaj se živciraš pa možda ne možeš učiti kak spada :D )
| Anonymous (napisa): | | lucky (napisa): | .... neznam da li ti ideš na predavanja i vježbe s ciljem da nešto naučiš ili samo zato što su obavezna i zato što moraš predat zadaće ???? ... ili pak ideš da vodiš brigu i statistiku tko je koliko puta izostao i tko je kad zadaću predao...
...i ja sam od onih koji su predavali svoje zadaće na vrijeme, a za ostale šta me briga...ja sam svoje obavila, a drugima ako nemogu pomoć neću im ni odmoć time da ih, kao ti, 'blatim' na forumu...kojeg profesor redovito posjećuje.... |
Naravno da idem da naucim nije to upitno u ovom slucaju. Ne znam imas li razloga za takav ton. (osim ako ti ne spadas u tu kategoriju)
Ali i dalje stojim iza toga da bi pravila trebala bit za sve ista zar ne ? Nepravda uvijek boli pa koliko god ona bila. Na kraju svake zadace lijepo pise krajnji rok za predaju iste.
Ne vodim statistiku samo poznam vecinu ljudi i imam dobro zapazanje.
Ne blatim nikog po imenu i prezimenu. Kao to je neki tabu pa se o tom ne smije pricat ili sto? |
Kaj tebe točno muči? tj. zakaj te to muči?
Da li to na bilo koji način utječe na tvoju ocjenu, znanje, ... ? (osim kaj se živciraš pa možda ne možeš učiti kak spada  )
|
|
| [Vrh] |
|
Gost
|
| Postano: 16:11 uto, 11. 1. 2011 Naslov: |
|
|
|
[quote="Buga."][quote="Anonymous"][quote="lucky"].... neznam da li ti ideš na predavanja i vježbe s ciljem da nešto naučiš ili samo zato što su obavezna i zato što moraš predat zadaće ???? ... ili pak ideš da vodiš brigu i statistiku tko je koliko puta izostao i tko je kad zadaću predao...
...i ja sam od onih koji su predavali svoje zadaće na vrijeme, a za ostale šta me briga...ja sam svoje obavila, a drugima ako nemogu pomoć neću im ni odmoć time da ih, kao ti, 'blatim' na forumu...kojeg profesor redovito posjećuje....[/quote]
Naravno da idem da naucim nije to upitno u ovom slucaju. Ne znam imas li razloga za takav ton. (osim ako ti ne spadas u tu kategoriju)
Ali i dalje stojim iza toga da bi pravila trebala bit za sve ista zar ne ? Nepravda uvijek boli pa koliko god ona bila. Na kraju svake zadace lijepo pise krajnji rok za predaju iste.
Ne vodim statistiku samo poznam vecinu ljudi i imam dobro zapazanje.
Ne blatim nikog po imenu i prezimenu. Kao to je neki tabu pa se o tom ne smije pricat ili sto?[/quote]
Kaj tebe točno muči? tj. zakaj te to muči?
Da li to na bilo koji način utječe na tvoju ocjenu, znanje, ... ? (osim kaj se živciraš pa možda ne možeš učiti kak spada :D )[/quote]
Ispricavam se ocito na krivom mjestu tipkam. Obratit cu se direktno asistentici ili profesoru u vezi toga. Ajde da nisi iz Zagreba pa jednu zadacu dvije nisi na vrijeme ali kad nis ne radis cijeli semestar i onda 5-6 zadaca doneses. Mene nije sram to rec, a siguran sam u svoje znanje tako da ..
Rok se mora postivati, ako ja postujem pobrinut cu se da i drugi.
| Buga. (napisa): | | Anonymous (napisa): | | lucky (napisa): | .... neznam da li ti ideš na predavanja i vježbe s ciljem da nešto naučiš ili samo zato što su obavezna i zato što moraš predat zadaće ???? ... ili pak ideš da vodiš brigu i statistiku tko je koliko puta izostao i tko je kad zadaću predao...
...i ja sam od onih koji su predavali svoje zadaće na vrijeme, a za ostale šta me briga...ja sam svoje obavila, a drugima ako nemogu pomoć neću im ni odmoć time da ih, kao ti, 'blatim' na forumu...kojeg profesor redovito posjećuje.... |
Naravno da idem da naucim nije to upitno u ovom slucaju. Ne znam imas li razloga za takav ton. (osim ako ti ne spadas u tu kategoriju)
Ali i dalje stojim iza toga da bi pravila trebala bit za sve ista zar ne ? Nepravda uvijek boli pa koliko god ona bila. Na kraju svake zadace lijepo pise krajnji rok za predaju iste.
Ne vodim statistiku samo poznam vecinu ljudi i imam dobro zapazanje.
Ne blatim nikog po imenu i prezimenu. Kao to je neki tabu pa se o tom ne smije pricat ili sto? |
Kaj tebe točno muči? tj. zakaj te to muči?
Da li to na bilo koji način utječe na tvoju ocjenu, znanje, ... ? (osim kaj se živciraš pa možda ne možeš učiti kak spada ) |
Ispricavam se ocito na krivom mjestu tipkam. Obratit cu se direktno asistentici ili profesoru u vezi toga. Ajde da nisi iz Zagreba pa jednu zadacu dvije nisi na vrijeme ali kad nis ne radis cijeli semestar i onda 5-6 zadaca doneses. Mene nije sram to rec, a siguran sam u svoje znanje tako da ..
Rok se mora postivati, ako ja postujem pobrinut cu se da i drugi.
|
|
| [Vrh] |
|
BeeBee
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
|
| [Vrh] |
|
lucky
Forumaš(ica)
Pridružen/a: 15. 12. 2010. (15:33:00)
Postovi: (14)16
|
|
| [Vrh] |
|
Juraj Siftar
Gost
|
| Postano: 17:51 uto, 11. 1. 2011 Naslov: |
|
|
|
U vezi s (nepravodobnim) predavanjem domaćih zadaća:
Da, postoji principijelni problem oko toga i baš smo kolegica Franušić
i ja više puta u zadnje vrijeme razgovarali o tome. Istina je da bi se
to moralo provoditi dosljedno i pravedno, a da smo mi katkad
previše popustljivi. Donekle je stvar u tome što evidentiranje predaje
zadaća nije sasvim ažurno, jer se ne predaju na jednom mjestu, a
pritom nitko od nas nije tako "tvrda srca" da će odbiti zadaću koja je
predana s "malim" (?) zakašnjenjem.
No, stvari i sa zadaćama i s testovima i ostalim obavezama stoje
zapravo tako da otprilike 80% studentica i studenata sve napravi
korektno i na vrijeme, ali onda dolaze "iznimke" - apeli da se iz
raznih razloga kriteriji "omekšaju" kako se ne bi izgubila godina
zbog "jedne sitnice" - par bodova na testovima, poneke (što može biti
i 5-6) nepravodobno predane zadaće i slično. Ja nastojim imati u
vidu cjelovitu sliku o nečijem radu, pa ako je netko npr. dobro riješio
1. kolokvij, a iz testova nedostaje par bodova, dopustim da piše
2. kolokvij pa ćemo vidjeti kako će napraviti i onda odlučiti o
ukupnom ishodu. U biti, ne želim da itko "otpadne" iz nekog
formalističkog razloga ili zbog lošeg dana ili bolesti ili nekog
drugog "sporednog" razloga. No, čim se počnu praviti iznimke,
onda je teško povući crtu. Moguće nezadovoljstvo onih koji uredno
ispunjavaju obaveze, a onda vide (jer popisi doista jesu javni, barem
još zasad) kako se "može i neuredno i nemarno", posve je opravdano
i pitanje se opravdano postavlja.
Moj opći odgovor u biti je takav da ni sam nisam zadovoljan
takvom situacijom, no držim se, po savjesti, načela da prvenstveno
ne smije biti oštećen pojedini student/studentica u konkretnom
slučaju, čak i ako su bili donekle nemarni. Istina je da su onda,
barem privremeno i indirektno, oštećeni oni koji jesu uredno sve
ispunjavali, no na kraju obično nekako "sve dođe na svoje".
Redoviti rad i učenje se isplati, jer se lakše, s manje stresova i
s više stvarnog znanja polaže ispit, dok neznanje i nerad ipak
"zapnu" u nekoj fazi, vrlo često tek na popravnom kolokviju
(što možda izgleda kasno, ali eto - imali ste sve šanse, pustio sam
vas koliko sam daleko mogao, no ako na kraju ipak niste pokazali
dostatno znanje - nema prolaza).
Dakle, ne želim da se dogodi da netko "izgubi godinu" ako je imao
loših dana ili ako je malo previše "dekoncentriran", "zablokiran" ili
slično, ali dokle god nekome na kraju ipak nije jasno što je
svojstvena vrijednost i svojstveni
vektor linearnog operatora te kako će ih izračunati,
onda nema prolaza na ispitu iz Linearne algebre 2,
barem ne dok ja
o tome odlučujem.
Znam da kompromisi često nisu idealna rješenja.
Juraj Šiftar
U vezi s (nepravodobnim) predavanjem domaćih zadaća:
Da, postoji principijelni problem oko toga i baš smo kolegica Franušić
i ja više puta u zadnje vrijeme razgovarali o tome. Istina je da bi se
to moralo provoditi dosljedno i pravedno, a da smo mi katkad
previše popustljivi. Donekle je stvar u tome što evidentiranje predaje
zadaća nije sasvim ažurno, jer se ne predaju na jednom mjestu, a
pritom nitko od nas nije tako "tvrda srca" da će odbiti zadaću koja je
predana s "malim" (?) zakašnjenjem.
No, stvari i sa zadaćama i s testovima i ostalim obavezama stoje
zapravo tako da otprilike 80% studentica i studenata sve napravi
korektno i na vrijeme, ali onda dolaze "iznimke" - apeli da se iz
raznih razloga kriteriji "omekšaju" kako se ne bi izgubila godina
zbog "jedne sitnice" - par bodova na testovima, poneke (što može biti
i 5-6) nepravodobno predane zadaće i slično. Ja nastojim imati u
vidu cjelovitu sliku o nečijem radu, pa ako je netko npr. dobro riješio
1. kolokvij, a iz testova nedostaje par bodova, dopustim da piše
2. kolokvij pa ćemo vidjeti kako će napraviti i onda odlučiti o
ukupnom ishodu. U biti, ne želim da itko "otpadne" iz nekog
formalističkog razloga ili zbog lošeg dana ili bolesti ili nekog
drugog "sporednog" razloga. No, čim se počnu praviti iznimke,
onda je teško povući crtu. Moguće nezadovoljstvo onih koji uredno
ispunjavaju obaveze, a onda vide (jer popisi doista jesu javni, barem
još zasad) kako se "može i neuredno i nemarno", posve je opravdano
i pitanje se opravdano postavlja.
Moj opći odgovor u biti je takav da ni sam nisam zadovoljan
takvom situacijom, no držim se, po savjesti, načela da prvenstveno
ne smije biti oštećen pojedini student/studentica u konkretnom
slučaju, čak i ako su bili donekle nemarni. Istina je da su onda,
barem privremeno i indirektno, oštećeni oni koji jesu uredno sve
ispunjavali, no na kraju obično nekako "sve dođe na svoje".
Redoviti rad i učenje se isplati, jer se lakše, s manje stresova i
s više stvarnog znanja polaže ispit, dok neznanje i nerad ipak
"zapnu" u nekoj fazi, vrlo često tek na popravnom kolokviju
(što možda izgleda kasno, ali eto - imali ste sve šanse, pustio sam
vas koliko sam daleko mogao, no ako na kraju ipak niste pokazali
dostatno znanje - nema prolaza).
Dakle, ne želim da se dogodi da netko "izgubi godinu" ako je imao
loših dana ili ako je malo previše "dekoncentriran", "zablokiran" ili
slično, ali dokle god nekome na kraju ipak nije jasno što je
svojstvena vrijednost i svojstveni
vektor linearnog operatora te kako će ih izračunati,
onda nema prolaza na ispitu iz Linearne algebre 2,
barem ne dok ja
o tome odlučujem.
Znam da kompromisi često nisu idealna rješenja.
Juraj Šiftar
|
|
| [Vrh] |
|
Gost
|
| Postano: 18:40 uto, 11. 1. 2011 Naslov: |
|
|
|
Eto drago mi je da se o tom vodi racuna. Sad mi je srce na mjestu :D
Kolege su me krivo shvatili. Nisam mislio da se sad nekog rusi zbog zadace (helouu i ja sam student, nisam idealan)
Ali ako postoji neki dogovor s pocetka semestra onda je dobro toga se drzati. Sto i je zapravo ideja Bolonjskog sustava da se pojedinim predmetima dodjeljuju ECTS bodovi na osnovi njihovog udjela u ukupnom studentovom radu,
što uključuje prisustvovanje nastavi, samostalni rad, pripremu za nastavu, učenje, izradu projekata i ostale aktivnosti potrebne za
savladavanje predmeta.....
Kad kazem "nepravda" onda se ona ne vidi jer se radi samo o zadacama koje formalno ne nose bodove. Ali se moze dogoditi da bas ti kolege nekako sakupe potrebnih 60 bodova na kolokvijima i prodju dalje bez obzira na zadace, a neki sve uredno rade i zbog tzv. loseg dana na kolokviju imaju 58-59 bodova i onda zavrse na popravnom jer dok ima popravnog nema dijeljenja bodova na zalbama. A onda tim studentima slijedi muka prava, cijelo gradivo od pocetka , teorija , zadaci, vjezbe....plus drugi kolegiji.
Eto samo toliko vazno da smo se razumijeli i lijepo je da se gleda sveukupan rad i da se to cijeni.
Eto drago mi je da se o tom vodi racuna. Sad mi je srce na mjestu
Kolege su me krivo shvatili. Nisam mislio da se sad nekog rusi zbog zadace (helouu i ja sam student, nisam idealan)
Ali ako postoji neki dogovor s pocetka semestra onda je dobro toga se drzati. Sto i je zapravo ideja Bolonjskog sustava da se pojedinim predmetima dodjeljuju ECTS bodovi na osnovi njihovog udjela u ukupnom studentovom radu,
što uključuje prisustvovanje nastavi, samostalni rad, pripremu za nastavu, učenje, izradu projekata i ostale aktivnosti potrebne za
savladavanje predmeta.....
Kad kazem "nepravda" onda se ona ne vidi jer se radi samo o zadacama koje formalno ne nose bodove. Ali se moze dogoditi da bas ti kolege nekako sakupe potrebnih 60 bodova na kolokvijima i prodju dalje bez obzira na zadace, a neki sve uredno rade i zbog tzv. loseg dana na kolokviju imaju 58-59 bodova i onda zavrse na popravnom jer dok ima popravnog nema dijeljenja bodova na zalbama. A onda tim studentima slijedi muka prava, cijelo gradivo od pocetka , teorija , zadaci, vjezbe....plus drugi kolegiji.
Eto samo toliko vazno da smo se razumijeli i lijepo je da se gleda sveukupan rad i da se to cijeni.
|
|
| [Vrh] |
|
Juraj Siftar
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Juraj Siftar
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ante003
Forumaš(ica)
Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol: 
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)
Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol:
|
| Postano: 19:16 sri, 12. 1. 2011 Naslov: |
|
|
|
Kaj se tiče rekurzivnih "uvodiš" još jednu trivijalnu jednadžbu F(n+1)=F(n+1). i zato je drugi redak 1 0
za tvoj primjer A bi bila {{-2, 1}, {1, 0}}.
Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz.
Kaj se tiče rekurzivnih "uvodiš" još jednu trivijalnu jednadžbu F(n+1)=F(n+1). i zato je drugi redak 1 0
za tvoj primjer A bi bila {{-2, 1}, {1, 0}}.
Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz.
_________________
No, you clearly don’t know who you’re talking to, so let me clue you in: I am not in danger, Skylar. I am the danger. A guy opens his door and gets shot and you think that of me? No. I am the one who knocks.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Serious Sam
Forumaš(ica)
Pridružen/a: 09. 12. 2009. (15:08:32)
Postovi: (5C)16
Spol:
|
|
| [Vrh] |
|
t-i-n-a_k-i-k-a
Forumaš(ica)
Pridružen/a: 13. 01. 2009. (12:45:44)
Postovi: (2C)16
|
|
| [Vrh] |
|
Serious Sam
Forumaš(ica)
Pridružen/a: 09. 12. 2009. (15:08:32)
Postovi: (5C)16
Spol:
|
|
| [Vrh] |
|
ante003
Forumaš(ica)
Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol:
|
| Postano: 21:10 sri, 12. 1. 2011 Naslov: |
|
|
|
[quote="Serious Sam"]Koliko ja znam, matrica prijelaza P je tu uvijek bila transponirana, a i tako smo radili na vjezbama.[/quote]
istina.
[quote]Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz.[/quote]
sorry, krivo postavio pitanje. Kad odredujem svojstvene vektore. dobijem vektor (3,2,1) recimo. jel ga trebam onda ortonormirat pa je taj ortonormirani vektor trazeni vektor ?
| Serious Sam (napisa): | | Koliko ja znam, matrica prijelaza P je tu uvijek bila transponirana, a i tako smo radili na vjezbama. |
istina.
| Citat: | | Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz. |
sorry, krivo postavio pitanje. Kad odredujem svojstvene vektore. dobijem vektor (3,2,1) recimo. jel ga trebam onda ortonormirat pa je taj ortonormirani vektor trazeni vektor ?
_________________
Ako ste previše otvorenog uma, ispast će vam mozak
------------------------------------------------------
Racunalo bez Windowsa je kao riba bez bicikla
|
|
| [Vrh] |
|
niky
Forumaš(ica)
Pridružen/a: 04. 11. 2008. (17:08:33)
Postovi: (2F)16
|
| Postano: 22:38 sri, 12. 1. 2011 Naslov: |
|
|
|
[quote="ante003"][quote="Serious Sam"]Koliko ja znam, matrica prijelaza P je tu uvijek bila transponirana, a i tako smo radili na vjezbama.[/quote]
istina.
[quote]Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz.[/quote]
sorry, krivo postavio pitanje. Kad odredujem svojstvene vektore. dobijem vektor (3,2,1) recimo. jel ga trebam onda ortonormirat pa je taj ortonormirani vektor trazeni vektor ?[/quote]
Kad nemas simetricnu m-cu onda ne znaci da ces dobit okomite vektore pa ih moras ortonormirat G-S postupkom. Ako dobijes ortogonalne onda ih samo treba normirat. Ali kod rekurzivnih jedn mozes samo nac P^1.
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Serious Sam"]Imam pitanje u vezi tih linearnih rekurzija drugog reda. Na vjezbama ih i nismo bas radili pa me nesto muci. Npr. jedna grupa od kolokvija iz 2009. ima 3. zadatak u kojem se trazi rješenje rekurzivne jednadzbe a_n+2 = 3 a_n+1 - a_n. U rješenjima kolokvija sam procitao da se rezultat dobija ako se pretpostavi da je a_n = alfa * (lambda 1)^n + beta * (lambda 2)^n gdje su lambda 1 i 2 dobivene svojstvene vrijednosti matrice A. Da li to opcenito vrijedi za sve rek. jednadzbe drugog reda kad trazimo rjesenje? Takoder, moze li mi netko objasniti kako su oni zakljucili da iz pocetnih uvjeta slijedi da je alfa = beta (ako znamo da je a_0 = 2 i a_1 = 3)?[/quote]
Vec je profesor odgovorio zasto se moze pretpostavit ta linearna kombinacija u nekom od prijasnjih postova.
Nisu zakljucili tek tako nego kad uvrstis sv.vrijenosti i pocetne uvjete u tu relaciju onda dobije da su alfa i beta jednake jedan, dakle izracunas
| ante003 (napisa): | | Serious Sam (napisa): | | Koliko ja znam, matrica prijelaza P je tu uvijek bila transponirana, a i tako smo radili na vjezbama. |
istina.
| Citat: | | Ne treba ortonormirat, osim ako ti je tako lakše odredit inverz. |
sorry, krivo postavio pitanje. Kad odredujem svojstvene vektore. dobijem vektor (3,2,1) recimo. jel ga trebam onda ortonormirat pa je taj ortonormirani vektor trazeni vektor ? |
Kad nemas simetricnu m-cu onda ne znaci da ces dobit okomite vektore pa ih moras ortonormirat G-S postupkom. Ako dobijes ortogonalne onda ih samo treba normirat. Ali kod rekurzivnih jedn mozes samo nac P^1.
Added after 3 minutes:
| Serious Sam (napisa): | | Imam pitanje u vezi tih linearnih rekurzija drugog reda. Na vjezbama ih i nismo bas radili pa me nesto muci. Npr. jedna grupa od kolokvija iz 2009. ima 3. zadatak u kojem se trazi rješenje rekurzivne jednadzbe a_n+2 = 3 a_n+1 - a_n. U rješenjima kolokvija sam procitao da se rezultat dobija ako se pretpostavi da je a_n = alfa * (lambda 1)^n + beta * (lambda 2)^n gdje su lambda 1 i 2 dobivene svojstvene vrijednosti matrice A. Da li to opcenito vrijedi za sve rek. jednadzbe drugog reda kad trazimo rjesenje? Takoder, moze li mi netko objasniti kako su oni zakljucili da iz pocetnih uvjeta slijedi da je alfa = beta (ako znamo da je a_0 = 2 i a_1 = 3)? |
Vec je profesor odgovorio zasto se moze pretpostavit ta linearna kombinacija u nekom od prijasnjih postova.
Nisu zakljucili tek tako nego kad uvrstis sv.vrijenosti i pocetne uvjete u tu relaciju onda dobije da su alfa i beta jednake jedan, dakle izracunas
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)
Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
| Postano: 22:49 sri, 12. 1. 2011 Naslov: |
|
|
|
[quote="ante003"]
Kad u sustavu rekurzivnih jednazbi odredujemo [latex]P^{-1}[/latex] ako matrica A nije simetrica, [b]jel treba svojstvene vektore izrazit ortonormirane ili ne ?[/b][/quote]
Odgovor na tvoje pitanje....
Ako matrica nije simetricna, mislim da ti je lakse izracunat [latex]P^{-1}[/latex] normalnim postupkom-tu mislim da racunas P*X=I, nego ortonormirat vektore po G-S,mislim kako hoces...A ako ih izrazis ortonormirane, onda je [latex]P^{-1}[/latex] jednostavno transponirana matrica P...Na tebi je da odlucis...da li ces radije radit nekoliko skalarnih produkata i normiranja i onda transponiranja ili ces jednostavno izracunat [latex]P^{-1}[/latex].
Jos jedan odgovor, naravno da svojstveni vektori nemoraju bit ortonormirani da bi se izracunala [latex]P^{-1}[/latex] , ali ako ih vec imas ortogonalne(sto je slucaj kada imas pocetnu matricu simetricnu), onda ih je lakse normirat, pa transponirat nego racunat [latex]P^{-1}[/latex].
Nadam se da sam pomogao.
| ante003 (napisa): |
Kad u sustavu rekurzivnih jednazbi odredujemo 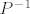 ako matrica A nije simetrica, jel treba svojstvene vektore izrazit ortonormirane ili ne ? |
Odgovor na tvoje pitanje....
Ako matrica nije simetricna, mislim da ti je lakse izracunat 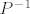normalnim postupkom-tu mislim da racunas P*X=I, nego ortonormirat vektore po G-S,mislim kako hoces...A ako ih izrazis ortonormirane, onda je 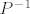jednostavno transponirana matrica P...Na tebi je da odlucis...da li ces radije radit nekoliko skalarnih produkata i normiranja i onda transponiranja ili ces jednostavno izracunat .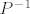
Jos jedan odgovor, naravno da svojstveni vektori nemoraju bit ortonormirani da bi se izracunala 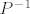, ali ako ih vec imas ortogonalne(sto je slucaj kada imas pocetnu matricu simetricnu), onda ih je lakse normirat, pa transponirat nego racunat .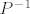
Nadam se da sam pomogao.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
