| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:14 čet, 13. 1. 2011 Naslov: Postano: 17:14 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Crazylamb1"]
ok, ali nije li to taj "gluplji" nacin sto si rekao? kako na ovaj jednostavniji? nije valjda da ak skuzis gledajuci crtez kako ide, da mozes samo odmah napisati rjesenje i gotovo..
jer ocito je gledajuci crtez da ima po 1 put svake duljine: prvo duljine 2, pa 5, pa 8, pa 11, ..., i tako samo dodajemo 3..
i to je to?
samo napisemo da je funkcija izvodnica t^2 + t^5 + t^8 + ... i to bi bilo to?[/quote]
Da, to je taj gluplji način. No i sam profesor je rekao da je ovaj "na prste" sasvim dovoljan, uz obrazloženje naravno. Nije ništa spominjao fju izvodnicu, tako da čak mislim da i to nije bilo potrebno napisati, samo dati objašnjenje da postoji jedinstven put duljine n ako i samo ako n==2(mod 3) i onda malo obrazložiti zašto :D
A za ovaj koeficijent uz x^3, samo se igraš sa množenjem redova. Ako imaš red [latex]a(x)=a_0+a_1x+...[/latex] i tražiš njegov multiplikativni inverz b, onda vrijedi [latex]a(x)\cdot b(x)=1[/latex], odnosno po komponentama:
[latex](a_0+a_1x+a_2 x^2 +a_3 x^3 +...) \cdot (b_0+b_1x+b_2 x^2+ b_3 x^3 +...)=1[/latex]
Kada grupiramo po potencijama imamo:
[latex]a_0b_0=1[/latex] (slobodan)
[latex]a_0b_1+a_1b_0=0[/latex] (uz x)
[latex]a_0b_2+a_1b_1+a_2b_0=0[/latex] (uz x^2)
[latex]a_0b_3+a_1b_2+a_2b_1+a_3b_0=0[/latex] (uz x^3)
Sad se samo riješi taj trokutasti sustav korak po korak, dok ne dođemo do b_3 :D
| Crazylamb1 (napisa): |
ok, ali nije li to taj "gluplji" nacin sto si rekao? kako na ovaj jednostavniji? nije valjda da ak skuzis gledajuci crtez kako ide, da mozes samo odmah napisati rjesenje i gotovo..
jer ocito je gledajuci crtez da ima po 1 put svake duljine: prvo duljine 2, pa 5, pa 8, pa 11, ..., i tako samo dodajemo 3..
i to je to?
samo napisemo da je funkcija izvodnica t^2 + t^5 + t^8 + ... i to bi bilo to? |
Da, to je taj gluplji način. No i sam profesor je rekao da je ovaj "na prste" sasvim dovoljan, uz obrazloženje naravno. Nije ništa spominjao fju izvodnicu, tako da čak mislim da i to nije bilo potrebno napisati, samo dati objašnjenje da postoji jedinstven put duljine n ako i samo ako n==2(mod 3) i onda malo obrazložiti zašto 
A za ovaj koeficijent uz x^3, samo se igraš sa množenjem redova. Ako imaš red 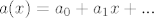 i tražiš njegov multiplikativni inverz b, onda vrijedi i tražiš njegov multiplikativni inverz b, onda vrijedi 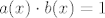 , odnosno po komponentama: , odnosno po komponentama:
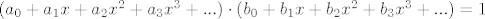
Kada grupiramo po potencijama imamo:
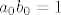 (slobodan) (slobodan)
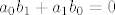 (uz x) (uz x)
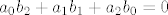 (uz x^2) (uz x^2)
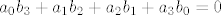 (uz x^3) (uz x^3)
Sad se samo riješi taj trokutasti sustav korak po korak, dok ne dođemo do b_3 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:26 čet, 13. 1. 2011 Naslov: Postano: 17:26 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Ančica"]Zna li itko kad će biti usmeni?[/quote]
Pitali smo profesora, ni on još točno ne zna... spominjao se neki termin početkom 2. mjeseca, ali još ništa nije službeno.
| Ančica (napisa): | | Zna li itko kad će biti usmeni? |
Pitali smo profesora, ni on još točno ne zna... spominjao se neki termin početkom 2. mjeseca, ali još ništa nije službeno.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
 Postano: 17:50 čet, 13. 1. 2011 Naslov: Postano: 17:50 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Luuka"]
A za ovaj koeficijent uz x^3, samo se igraš sa množenjem redova. Ako imaš red [latex]a(x)=a_0+a_1x+...[/latex] i tražiš njegov multiplikativni inverz b, onda vrijedi [latex]a(x)\cdot b(x)=1[/latex], odnosno po komponentama:
[latex](a_0+a_1x+a_2 x^2 +a_3 x^3 +...) \cdot (b_0+b_1x+b_2 x^2+ b_3 x^3 +...)=1[/latex]
Kada grupiramo po potencijama imamo:
[latex]a_0b_0=1[/latex] (slobodan)
[latex]a_0b_1+a_1b_0=0[/latex] (uz x)
[latex]a_0b_2+a_1b_1+a_2b_0=0[/latex] (uz x^2)
[latex]a_0b_3+a_1b_2+a_2b_1+a_3b_0=0[/latex] (uz x^3)
Sad se samo riješi taj trokutasti sustav korak po korak, dok ne dođemo do b_3 :D[/quote]
ok, ja rjesavam taj sustav...i za b3 dobijem izraz koji ima u sebi a0, a1, a2 i a3, ali u zadanom zadatku imamo samo a0, a1, a2 (a, b, c)..mora da nesto krivo radim...je li tocno ono rjesenje sto je ekatarina stavila?
| Luuka (napisa): |
A za ovaj koeficijent uz x^3, samo se igraš sa množenjem redova. Ako imaš red 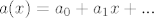 i tražiš njegov multiplikativni inverz b, onda vrijedi i tražiš njegov multiplikativni inverz b, onda vrijedi 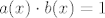 , odnosno po komponentama: , odnosno po komponentama:
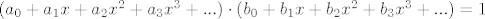
Kada grupiramo po potencijama imamo:
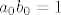 (slobodan) (slobodan)
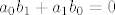 (uz x) (uz x)
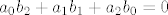 (uz x^2) (uz x^2)
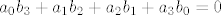 (uz x^3) (uz x^3)
Sad se samo riješi taj trokutasti sustav korak po korak, dok ne dođemo do b_3  |
ok, ja rjesavam taj sustav...i za b3 dobijem izraz koji ima u sebi a0, a1, a2 i a3, ali u zadanom zadatku imamo samo a0, a1, a2 (a, b, c)..mora da nesto krivo radim...je li tocno ono rjesenje sto je ekatarina stavila?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
 Postano: 18:05 čet, 13. 1. 2011 Naslov: Postano: 18:05 čet, 13. 1. 2011 Naslov: |
    |
|
|
@Luuka - e pa i ja to isto dobijem, ali me zbunjuje jer u zadatku u pocetnom formalnom redu imamo samo 3 clana (a, b, c ili a0, a1, a2) - a i kad gledam rjesenje koje dobije ekatarina, nije ni blizu...ono, hocu da predjem s oznaka a0, a1, a2 na a, b, c, ali me buni taj a3 kad mi nemamo d ili nesto slicno...
@Luuka - e pa i ja to isto dobijem, ali me zbunjuje jer u zadatku u pocetnom formalnom redu imamo samo 3 clana (a, b, c ili a0, a1, a2) - a i kad gledam rjesenje koje dobije ekatarina, nije ni blizu...ono, hocu da predjem s oznaka a0, a1, a2 na a, b, c, ali me buni taj a3 kad mi nemamo d ili nesto slicno...
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:10 čet, 13. 1. 2011 Naslov: Postano: 18:10 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Crazylamb1"]@Luuka - e pa i ja to isto dobijem, ali me zbunjuje jer u zadatku u pocetnom formalnom redu imamo samo 3 clana (a, b, c ili a0, a1, a2) - a i kad gledam rjesenje koje dobije ekatarina, nije ni blizu...ono, hocu da predjem s oznaka a0, a1, a2 na a, b, c, ali me buni taj a3 kad mi nemamo d ili nesto slicno...[/quote]
Ja rješavao općenito, nisam ni pogledo zadatak :lol: :lol:
U našem zadatku je a_3=0 ( nema koeficijenta uz x^3 ) pa se formula pojednostavljuje i dobijemo isto ko ekatarina :D
| Crazylamb1 (napisa): | | @Luuka - e pa i ja to isto dobijem, ali me zbunjuje jer u zadatku u pocetnom formalnom redu imamo samo 3 clana (a, b, c ili a0, a1, a2) - a i kad gledam rjesenje koje dobije ekatarina, nije ni blizu...ono, hocu da predjem s oznaka a0, a1, a2 na a, b, c, ali me buni taj a3 kad mi nemamo d ili nesto slicno... |
Ja rješavao općenito, nisam ni pogledo zadatak  
U našem zadatku je a_3=0 ( nema koeficijenta uz x^3 ) pa se formula pojednostavljuje i dobijemo isto ko ekatarina 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
|
| [Vrh] |
|
aauk
Forumaš(ica)

Pridružen/a: 18. 02. 2007. (17:11:01)
Postovi: (18)16
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
 Postano: 18:29 čet, 13. 1. 2011 Naslov: Postano: 18:29 čet, 13. 1. 2011 Naslov: |
    |
|
|
Ja u 5. nisam koristila binomni razvoj, gdje se to korisiti luuka?
Dobila sam iz Lagr.formule da je trazeni clan 1/2 onoga sto stoji uz x u redu ( x/f(x) )^2.
na kraju : -1/beta^3
@cr
U skripti iz diskretne, koja je na netu pretpostavljam, imas na pocetku neke kombinatorne dokaze, to si pogledaj, pa ce ti biti jasno. A imas i jedan koji je Luuka dao negdje na ovoj temi
Ja u 5. nisam koristila binomni razvoj, gdje se to korisiti luuka?
Dobila sam iz Lagr.formule da je trazeni clan 1/2 onoga sto stoji uz x u redu ( x/f(x) )^2.
na kraju : -1/beta^3
@cr
U skripti iz diskretne, koja je na netu pretpostavljam, imas na pocetku neke kombinatorne dokaze, to si pogledaj, pa ce ti biti jasno. A imas i jedan koji je Luuka dao negdje na ovoj temi
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:29 čet, 13. 1. 2011 Naslov: Postano: 18:29 čet, 13. 1. 2011 Naslov: |
    |
|
|
To se zna dešavat, samo refreshaj stranicu koji put :D
@CrazyLamb Formula je dosta trivijalna, lako se vidi da je to ustvari [latex](1+2)^n[/latex]. A kombinatorna interpertacija vjerojatno nešto preko funkcija (desno je broj svih funkcija sa n-članog u tročlani skup)
@ekatarina A da, tu moguće ne treba binomni razvoj, ne zanima nas cijeli red, samo jedan koeficijent. Moj bad :D
To se zna dešavat, samo refreshaj stranicu koji put 
@CrazyLamb Formula je dosta trivijalna, lako se vidi da je to ustvari 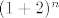 . A kombinatorna interpertacija vjerojatno nešto preko funkcija (desno je broj svih funkcija sa n-članog u tročlani skup) . A kombinatorna interpertacija vjerojatno nešto preko funkcija (desno je broj svih funkcija sa n-članog u tročlani skup)
@ekatarina A da, tu moguće ne treba binomni razvoj, ne zanima nas cijeli red, samo jedan koeficijent. Moj bad 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
frances
Forumaš(ica)
Pridružen/a: 15. 07. 2006. (18:27:06)
Postovi: (39)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
 Postano: 20:06 čet, 13. 1. 2011 Naslov: Postano: 20:06 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="ekatarina"]
Dobila sam iz Lagr.formule da je trazeni clan 1/2 onoga sto stoji uz x u redu ( x/f(x) )^2.
na kraju : -1/beta^3
[/quote]
ev natrag na posao (moralo se ici do menze :D) - ja isto dobijem to iz lagr. formule..
a kako onda dobijes to sto je uz x? ja pokratim x u brojniku i nazivniku, pa mi ostane 1/BETA+GAMAx (i to sve na kvadrat, naravno).
e sad, da se dobije to sto je uz x, je li treba ono suma j>=0, (-2 choose j) * BETA^(-2-j)*(GAMAx)^j (drugim rijecima, binomna formula)? ako treba - sto dalje, ako ne treba to - kako se nadje to sto je uz x?
| ekatarina (napisa): |
Dobila sam iz Lagr.formule da je trazeni clan 1/2 onoga sto stoji uz x u redu ( x/f(x) )^2.
na kraju : -1/beta^3
|
ev natrag na posao (moralo se ici do menze  ) - ja isto dobijem to iz lagr. formule.. ) - ja isto dobijem to iz lagr. formule..
a kako onda dobijes to sto je uz x? ja pokratim x u brojniku i nazivniku, pa mi ostane 1/BETA+GAMAx (i to sve na kvadrat, naravno).
e sad, da se dobije to sto je uz x, je li treba ono suma j>=0, (-2 choose j) * BETA^(-2-j)*(GAMAx)^j (drugim rijecima, binomna formula)? ako treba - sto dalje, ako ne treba to - kako se nadje to sto je uz x?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|






















