| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Dama Herc
Forumaš(ica)

Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:58 čet, 30. 12. 2010 Naslov: Postano: 21:58 čet, 30. 12. 2010 Naslov: |
    |
|
|
(a) Sustav AX = B ima jedinstveno rješenje, pa i njegov pripadni homogeni sustav AX = 0 ima jedinstveno rješenje. Znamo da je [latex]\dim \Omega = n - r(A)[/latex]. Dakle, [latex]r(A) = n - \dim \Omega = n - \dim \{0\} = n - 0 = n[/latex].
(b) Kako smo već zaključili u (a), homogeni sustav AX = 0 ima jedinstveno rješenje. Općenito je skup rješenja sustava AX = B' linearna mnogostrukost [latex]C_0 + \Omega[/latex], gdje je [latex]C_0[/latex] neko rješenje tog sustava. Konkretno, [latex]C_0 + \Omega = C_0 + \{0\} = \{C_0\}[/latex]. Dakle, sustav AX = B' ili ima jedinstveno rješenje ili nema rješenja, tj. ima najviše jedno rješenje.
(c) Tu imaš tipfeler. Treba dokazati da je [latex]m \geq n[/latex].
Vrijedi [latex]r(A) \leq \min\{m, n\}[/latex]. Dakle, [latex]m \geq r(A)\stackrel{(a)}{=} n[/latex].
Bio sam dosta sažet, pa slobodno reci ako treba nešto razjasniti. :)
(a) Sustav AX = B ima jedinstveno rješenje, pa i njegov pripadni homogeni sustav AX = 0 ima jedinstveno rješenje. Znamo da je 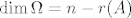 . Dakle, . Dakle, 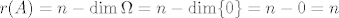 . .
(b) Kako smo već zaključili u (a), homogeni sustav AX = 0 ima jedinstveno rješenje. Općenito je skup rješenja sustava AX = B' linearna mnogostrukost  , gdje je , gdje je 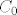 neko rješenje tog sustava. Konkretno, neko rješenje tog sustava. Konkretno, 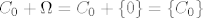 . Dakle, sustav AX = B' ili ima jedinstveno rješenje ili nema rješenja, tj. ima najviše jedno rješenje. . Dakle, sustav AX = B' ili ima jedinstveno rješenje ili nema rješenja, tj. ima najviše jedno rješenje.
(c) Tu imaš tipfeler. Treba dokazati da je  . .
Vrijedi 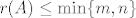 . Dakle, . Dakle, 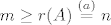 . .
Bio sam dosta sažet, pa slobodno reci ako treba nešto razjasniti. 
|
|
| [Vrh] |
|
Dama Herc
Forumaš(ica)

Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 16:00 ned, 16. 1. 2011 Naslov: Postano: 16:00 ned, 16. 1. 2011 Naslov: |
    |
|
|
Moze pomoc oko drugog zadatka s tog istog kolokvija:
2XF + G = H^t (H transponirano)
Ne razumijem sto zeli reci "nađite [b]SVE[/b] matrice X za koje to vrijedi",
bas nesto slicno da smo vjezbali na vjezbamo nisam nasla, al po mom nekom skromnom znanju, ja sam isla rejsavati sljedecim postupkom...
1. 2X=H^t - G (to se da lijepo izracunati)
2. Razliku na desnoj strani podijelim s 2, znaci svaki element podijelim s 2
3. Sad znam da je F regularna matrica (kvadratna je i det ne iznosi 0) pa
postoji inverz te matrice.
( F : I ) (tim postupkom dolazim do inverza)
4. Sad: sad pomnozim lijevu i desnu stranu s tim inverzom i tako dobijem X.
To je meni nekako logicno al mislim da negdje grijesim, ali ne znam gdje. Zar nije rjesenje jedinstveno?
Hvala.
Moze pomoc oko drugog zadatka s tog istog kolokvija:
2XF + G = H^t (H transponirano)
Ne razumijem sto zeli reci "nađite SVE matrice X za koje to vrijedi",
bas nesto slicno da smo vjezbali na vjezbamo nisam nasla, al po mom nekom skromnom znanju, ja sam isla rejsavati sljedecim postupkom...
1. 2X=H^t - G (to se da lijepo izracunati)
2. Razliku na desnoj strani podijelim s 2, znaci svaki element podijelim s 2
3. Sad znam da je F regularna matrica (kvadratna je i det ne iznosi 0) pa
postoji inverz te matrice.
( F : I ) (tim postupkom dolazim do inverza)
4. Sad: sad pomnozim lijevu i desnu stranu s tim inverzom i tako dobijem X.
To je meni nekako logicno al mislim da negdje grijesim, ali ne znam gdje. Zar nije rjesenje jedinstveno?
Hvala.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:59 ned, 16. 1. 2011 Naslov: Postano: 18:59 ned, 16. 1. 2011 Naslov: |
    |
|
|
Imaš dosta matematičkog software-a. Neki se plaćaju (Mathematica, Matlab...), dok neki ne (Maxima...).
Ako ti se neda nabavljati, imaš [url=http://www.wolframalpha.com/]Wolfram Alphu[/url].
Prvo da objasnim kako se prikazuju matrice u Mathematici i Wolfram Alphi. U njima postoje strukture zvane liste, npr. {1, 2, 3}. Dakle, nabrojiš sve elemente i zatvoriš u vitičaste zagrade. Matrice su liste listi, npr. [latex]\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}[/latex] zapisujemo s {{1, 2}, {3, 4}}.
Za LU rastav imaš funkciju LUDecomposition. Ako želiš saznati LU rastav gore spomenute matrice, u Wolfram Alphu upišeš LUDecomposition[{{1, 2}, {3, 4}}].
Operator množenja je točka za kraj rečenice.
Rješavati sustave možeš pomoću funkcije Solve. Za riješiti sustav [latex]\left\{ \begin{array}{l}
x + y = 2 \\
2 x + 3 y = 8
\end{array} \right.[/latex] trebaš upisati Solve[{x + y = 2, 2 x + 3 y = 8}, {x, y}]. Primijeti da nije potrebno pisati * za množenje brojeva.
Još neke korisne funkcije su Det, Inverse i MatrixRank. Mislim da možeš pogoditi što rade. :)
Imaš dosta matematičkog software-a. Neki se plaćaju (Mathematica, Matlab...), dok neki ne (Maxima...).
Ako ti se neda nabavljati, imaš Wolfram Alphu.
Prvo da objasnim kako se prikazuju matrice u Mathematici i Wolfram Alphi. U njima postoje strukture zvane liste, npr. {1, 2, 3}. Dakle, nabrojiš sve elemente i zatvoriš u vitičaste zagrade. Matrice su liste listi, npr. 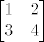 zapisujemo s {{1, 2}, {3, 4}}. zapisujemo s {{1, 2}, {3, 4}}.
Za LU rastav imaš funkciju LUDecomposition. Ako želiš saznati LU rastav gore spomenute matrice, u Wolfram Alphu upišeš LUDecomposition[{{1, 2}, {3, 4}}].
Operator množenja je točka za kraj rečenice.
Rješavati sustave možeš pomoću funkcije Solve. Za riješiti sustav 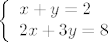 trebaš upisati Solve[{x + y = 2, 2 x + 3 y = 8}, {x, y}]. Primijeti da nije potrebno pisati * za množenje brojeva. trebaš upisati Solve[{x + y = 2, 2 x + 3 y = 8}, {x, y}]. Primijeti da nije potrebno pisati * za množenje brojeva.
Još neke korisne funkcije su Det, Inverse i MatrixRank. Mislim da možeš pogoditi što rade. 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
 Postano: 1:08 sub, 22. 1. 2011 Naslov: Postano: 1:08 sub, 22. 1. 2011 Naslov: |
    |
|
|
[quote="A-tom"]Koji je odg na 5. zadatak iz ovogodisnjeg kolokvija?
Rang matrrice 5x5 je 2. Pokzaite da Ax=0 i A(transponirano)x=0 imaju barem jedno ne trivijalno rjesenje,[/quote]
Iz ranga znamo da je dimenzija homogenog sustava rješenja 5-2=3. Transponiranje ne mijenja rang pa je i rang homogenog sustava transponirane matrice 3. Iz one formule iz prvog semestra znamo da je dimenzija presjeka = dimenzija prvog + dimenzija drugog - dimenzija zbroj, a kako znamo da je dimenzija zbroja sigurno manja ili jednaka od 5, slijedi da je dimenzija presjeka = 3+3-dimenzija zbroja => (veće ili jednako) 3+3-5=1, dakle presjek im nije nulprostor, pa postoje i netrivijalni vektori u presjeku, pa zato i netrivijalna rješenja.
| A-tom (napisa): | Koji je odg na 5. zadatak iz ovogodisnjeg kolokvija?
Rang matrrice 5x5 je 2. Pokzaite da Ax=0 i A(transponirano)x=0 imaju barem jedno ne trivijalno rjesenje, |
Iz ranga znamo da je dimenzija homogenog sustava rješenja 5-2=3. Transponiranje ne mijenja rang pa je i rang homogenog sustava transponirane matrice 3. Iz one formule iz prvog semestra znamo da je dimenzija presjeka = dimenzija prvog + dimenzija drugog - dimenzija zbroj, a kako znamo da je dimenzija zbroja sigurno manja ili jednaka od 5, slijedi da je dimenzija presjeka = 3+3-dimenzija zbroja ⇒ (veće ili jednako) 3+3-5=1, dakle presjek im nije nulprostor, pa postoje i netrivijalni vektori u presjeku, pa zato i netrivijalna rješenja.
_________________
Ceterum censeo Carthaginem esse delendam.
|
|
| [Vrh] |
|
|












