| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
 Postano: 12:28 pon, 17. 1. 2011 Naslov: Postano: 12:28 pon, 17. 1. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]Molila bih nekoga ko je na faksu da ak dodu rezultati javi to i po mogucnosti fotka i stavi ovdje.[/quote]
Potpisujem.
Ja cu biti sutra (18.) i onda 20. na faxu, pa ak budu rezultati nekad tad, ja cu staviti ovdje. Ako ne budu tad, tek opet idem 24. a valjda ce (nadam se) prije toga biti rezultati, pa neka ih, molim vas, netko drugi stavi.
Tko prvi - njegova sarma :P :D
| Anonymous (napisa): | | Molila bih nekoga ko je na faksu da ak dodu rezultati javi to i po mogucnosti fotka i stavi ovdje. |
Potpisujem.
Ja cu biti sutra (18.) i onda 20. na faxu, pa ak budu rezultati nekad tad, ja cu staviti ovdje. Ako ne budu tad, tek opet idem 24. a valjda ce (nadam se) prije toga biti rezultati, pa neka ih, molim vas, netko drugi stavi.
Tko prvi - njegova sarma  
|
|
| [Vrh] |
|
lyra
Forumaš(ica)

Pridružen/a: 17. 07. 2006. (21:23:44)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
|
| [Vrh] |
|
lepi
Forumaš(ica)

Pridružen/a: 07. 06. 2007. (17:04:06)
Postovi: (21)16
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
Jaja
Forumaš(ica)


Pridružen/a: 26. 09. 2004. (12:06:48)
Postovi: (C3)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
DanijelM
Forumaš(ica)

Pridružen/a: 20. 02. 2008. (11:56:05)
Postovi: (29)16
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
__fox
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (20:00:38)
Postovi: (35)16
Spol: 
|
 Postano: 14:13 čet, 20. 1. 2011 Naslov: Postano: 14:13 čet, 20. 1. 2011 Naslov: |
    |
|
|
ev za sve vas i nas koji refreshiramo forum cekajuci rezultate imam najnoviju informaciju. naime, frend je sad bio na faxu, sreo je prof na hodniku koji se jako zurio nekamo. spiska jos uvijek nema. kolokviji se mogu kod njega pogledati 10tak min prije 17h. onda profesora nema od 17-19h (ispit neki nesta) i od 19h pa nadalje (ovo nadalje je upitno do kad :lol:) se opet moze kod profesora gledat kolokvij :D
profesor ima puno posla, ispravlja kolokvije, neke zadace, i jos tisuce stvari tako da ne stigne napisat i stavit listu na vrata, barem nece gotovo sigurno do poslije 19h stavit (infinitezimalno mala vjerojatnost da ce napisat listu i stavit ju na vrata onih 10min prije 17h). eto, sad na miru mozete ucit aktuarsku :D sretno svima ,) pozz
ev za sve vas i nas koji refreshiramo forum cekajuci rezultate imam najnoviju informaciju. naime, frend je sad bio na faxu, sreo je prof na hodniku koji se jako zurio nekamo. spiska jos uvijek nema. kolokviji se mogu kod njega pogledati 10tak min prije 17h. onda profesora nema od 17-19h (ispit neki nesta) i od 19h pa nadalje (ovo nadalje je upitno do kad  ) se opet moze kod profesora gledat kolokvij ) se opet moze kod profesora gledat kolokvij 
profesor ima puno posla, ispravlja kolokvije, neke zadace, i jos tisuce stvari tako da ne stigne napisat i stavit listu na vrata, barem nece gotovo sigurno do poslije 19h stavit (infinitezimalno mala vjerojatnost da ce napisat listu i stavit ju na vrata onih 10min prije 17h). eto, sad na miru mozete ucit aktuarsku  sretno svima ,) pozz sretno svima ,) pozz
|
|
| [Vrh] |
|
d@nijel
Forumaš(ica)


Pridružen/a: 17. 07. 2006. (13:42:56)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 22:18 čet, 20. 1. 2011 Naslov: Postano: 22:18 čet, 20. 1. 2011 Naslov: |
    |
|
|
Evo, ja cu :D
5. Uocimo da je [latex](\log \frac{1}{1-x})' = \frac{1}{1-x}[/latex] Pa odmah slijedi da je [latex]\log \frac{1}{1-x} = \sum_{i \geq 1} \frac{x^i}{i} = \sum_{i \geq 1} (i-1)! \frac{x^i}{i!}[/latex], odnosno ovo je EFI niza [latex]a_n=(n-1)![/latex] za [latex]n \geq 1[/latex], a znamo da tocno toliko ima ciklickih permutacija skupa [latex]\{1,\dots,n\}[/latex]. Uocimo jos da je nulti clan 0, sto se podudara sa onim u eksponencijalnoj formuli. A ona kaze da je [latex]e^{f(x)}[/latex] EFI niza [latex]h(n)=h_n[/latex] gdje je [latex]h(\# X)=\sum_{\{ B_1, \dots , B_k \} \in \Pi (X)} f(\# B_1) f(\# B_2) \cdots f(\# B_k)[/latex]. Direktno iz [latex]e^{\log \frac{1}{1-x}} = \frac{1}{1-x}=\sum_{i \geq 0} x^î = \sum_{i \geq 0} i! \frac{x^î}{i!}[/latex] imamo da je niz [latex]h_n=n![/latex]. Sad to samo treba interpretirati. Naime, [latex]h_n[/latex] je broj nacina da na n-clanom skupu napravimo particiju i onda na svakoj particiji nacinimo ciklicku strukturu. Dakle, pokazali smo zapravo da permutacija koje se raspadju na disjunktne cikluse ima n!, ilitiga da je svaka permutacija takva.
7. Ovo je doslovno samo uvrstavanje. Möbiusova fja se definira kao [latex]\mu (x,x)=1[/latex] i onda rekurzivno [latex]\mu (x,y) = - \sum_{x | z | y , z \neq y} \mu (x,z)[/latex] za [latex]x|y,x \neq y[/latex], jasno ako [latex]x \nmid y[/latex] onda po definiciji mora biti [latex]\mu (x,y) = 0[/latex]. Sada se izracuna da je:
[latex]\mu (1,1) = \mu (2,2) = \mu (7,7) = \mu (14,14) = \mu (1,14) = 1[/latex] i [latex]\mu (1,7) = \mu (1,2) = \mu (2,14) = \mu (7,14) = -1[/latex].
Evo, ja cu 
5. Uocimo da je 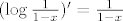 Pa odmah slijedi da je Pa odmah slijedi da je 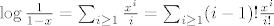 , odnosno ovo je EFI niza , odnosno ovo je EFI niza 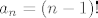 za za 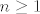 , a znamo da tocno toliko ima ciklickih permutacija skupa , a znamo da tocno toliko ima ciklickih permutacija skupa  . Uocimo jos da je nulti clan 0, sto se podudara sa onim u eksponencijalnoj formuli. A ona kaze da je . Uocimo jos da je nulti clan 0, sto se podudara sa onim u eksponencijalnoj formuli. A ona kaze da je 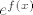 EFI niza EFI niza 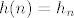 gdje je gdje je 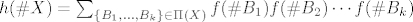 . Direktno iz . Direktno iz 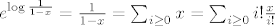 imamo da je niz imamo da je niz 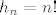 . Sad to samo treba interpretirati. Naime, . Sad to samo treba interpretirati. Naime, 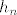 je broj nacina da na n-clanom skupu napravimo particiju i onda na svakoj particiji nacinimo ciklicku strukturu. Dakle, pokazali smo zapravo da permutacija koje se raspadju na disjunktne cikluse ima n!, ilitiga da je svaka permutacija takva. je broj nacina da na n-clanom skupu napravimo particiju i onda na svakoj particiji nacinimo ciklicku strukturu. Dakle, pokazali smo zapravo da permutacija koje se raspadju na disjunktne cikluse ima n!, ilitiga da je svaka permutacija takva.
7. Ovo je doslovno samo uvrstavanje. Möbiusova fja se definira kao 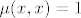 i onda rekurzivno i onda rekurzivno 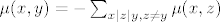 za za 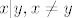 , jasno ako , jasno ako 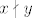 onda po definiciji mora biti onda po definiciji mora biti 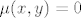 . Sada se izracuna da je: . Sada se izracuna da je:
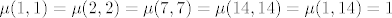 i i 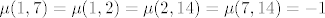 . .
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
Jaja
Forumaš(ica)


Pridružen/a: 26. 09. 2004. (12:06:48)
Postovi: (C3)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
d@nijel
Forumaš(ica)


Pridružen/a: 17. 07. 2006. (13:42:56)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
teh_pwnerer
Forumaš(ica)
Pridružen/a: 02. 02. 2006. (19:06:27)
Postovi: (62)16
|
 Postano: 11:20 pon, 24. 1. 2011 Naslov: Postano: 11:20 pon, 24. 1. 2011 Naslov: |
    |
|
|
[quote="teh_pwnerer"]Jel bi mogla koja dobra duša ovih dana ostavit u skriptarnici na kopiranje bilježnicu iz kombinatorike? Hvala[/quote]
Ja bi ponovio svoju molbu, činim štogod treba da se domognem bilježaka, dajem novac, kupujem pive, slaje, slatkiše, štagod :D (treba mi zadnjih nekoliko predavanja)
| teh_pwnerer (napisa): | | Jel bi mogla koja dobra duša ovih dana ostavit u skriptarnici na kopiranje bilježnicu iz kombinatorike? Hvala |
Ja bi ponovio svoju molbu, činim štogod treba da se domognem bilježaka, dajem novac, kupujem pive, slaje, slatkiše, štagod  (treba mi zadnjih nekoliko predavanja) (treba mi zadnjih nekoliko predavanja)
|
|
| [Vrh] |
|
squirrel
Forumaš(ica)

Pridružen/a: 29. 01. 2007. (22:38:42)
Postovi: (12)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
















