| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:54 pet, 22. 4. 2011 Naslov: Postano: 18:54 pet, 22. 4. 2011 Naslov: |
    |
|
|
Stvar je krajnje besmislena, tako da dajem samo neku generalnu ideju, pa ako si primjereni mazohist, izvest ćeš to korak po korak. :) WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto:
ja sam na početku bio mudar, pa sam napisao funkciju koju integriramo kao [latex]\displaystyle\frac{x}{3}\cdot\frac{3x^2}{(x^3+1)^2}[/latex]. Može se i bez toga sigurno, ali ovo ipak ponešto olakšava. :) Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom [latex]t=x^3[/latex]), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor :D) na računanje integrala funkcije[latex]\displaystyle\frac{1}{x^3+1}[/latex]. E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: [latex]\displaystyle\frac{1}{x^3+1}=\frac{1}{3}(\frac{2-x}{x^2-x+1}+\frac{1}{x+1})[/latex]. Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da. :D Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi. :)
Stvar je krajnje besmislena, tako da dajem samo neku generalnu ideju, pa ako si primjereni mazohist, izvest ćeš to korak po korak.  WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto: WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto:
ja sam na početku bio mudar, pa sam napisao funkciju koju integriramo kao 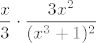 . Može se i bez toga sigurno, ali ovo ipak ponešto olakšava. . Može se i bez toga sigurno, ali ovo ipak ponešto olakšava.  Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom 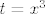 ), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor ), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor  ) na računanje integrala funkcije ) na računanje integrala funkcije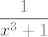 . E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: . E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: 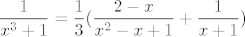 . Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da. . Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da.  Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi. Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi. 
Zadnja promjena: mornik; 7:02 sub, 23. 4. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
 Postano: 19:41 pet, 22. 4. 2011 Naslov: Postano: 19:41 pet, 22. 4. 2011 Naslov: |
    |
|
|
[quote="mornik"]Stvar je krajnje besmislena, tako da dajem samo neku generalnu ideju, pa ako si primjereni mazohist, izvest ćeš to korak po korak. :) WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto:
ja sam na početku bio mudar, pa sam napisao funkciju koju integriramo kao [latex]\displaystyle\frac{x}{3}\cdot\frac{3x^2}{(x^3+1)^2}[/latex]. Može se i bez toga sigurno, ali ovo ipak ponešto olakšava. :) Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom [latex]t=x^3[/latex]), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor :D) na računanje integrala funkcije[latex]\displaystyle\frac{x}{x^3+1}[/latex]. E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: [latex]\displaystyle\frac{x}{x^3+1}=\frac{1}{3}(\frac{x+1}{x^2-x+1}-\frac{1}{x+1})[/latex]. Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da. :D Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi. :)[/quote]
Kako si ti pod integralom dobio x/(x^3 + 1)? Kad sam x/3 derivirao dobio sam 1/3, a kad sam 3x^2/(x^3+1)^2 integrirao dobijem -1/(x^3+1). I onda mi ispada sljedeće (po onoj parcijalnoj formuli) -x/[3(x^3+1)] |(0 do 1) + 1/3*integral od 1/(x^3+1)dx. Jesam li negdje možda pogriješio ili tako treba ispasti?
| mornik (napisa): | Stvar je krajnje besmislena, tako da dajem samo neku generalnu ideju, pa ako si primjereni mazohist, izvest ćeš to korak po korak.  WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto: WolframAlpha nudi razne ideje, ovisno o tome kako mu postaviš pitanje, ali sve se na kraju svodi na isto:
ja sam na početku bio mudar, pa sam napisao funkciju koju integriramo kao 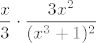 . Može se i bez toga sigurno, ali ovo ipak ponešto olakšava. . Može se i bez toga sigurno, ali ovo ipak ponešto olakšava.  Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom Sad, lijevi faktor nam je lako derivirati, a desni integrirati (možeš i napamet, a možeš i sa supstitucijom 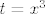 ), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor ), pa se stvar lako svede (uz neki broj koji još dobiješ kao pribrojnik i još valjda nekakav faktor  ) na računanje integrala funkcije ) na računanje integrala funkcije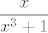 . E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: . E, a tu nećemo moći biti pretjerano pametni: jedina se donekle razumna opcija čini rastaviti stvar na parcijalne razlomke: 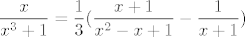 . Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da. . Sad ti preostaje to integrirati, a to ste radili na vježbama. Ogavno je, da.  Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi. Nadam se da je bilo od pomoći, a ako treba pomoći završiti ili neki korak izvesti, javi.  |
Kako si ti pod integralom dobio x/(x^3 + 1)? Kad sam x/3 derivirao dobio sam 1/3, a kad sam 3x^2/(x^3+1)^2 integrirao dobijem -1/(x^3+1). I onda mi ispada sljedeće (po onoj parcijalnoj formuli) -x/[3(x^3+1)] |(0 do 1) + 1/3*integral od 1/(x^3+1)dx. Jesam li negdje možda pogriješio ili tako treba ispasti?
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 11:50 sub, 23. 4. 2011 Naslov: Postano: 11:50 sub, 23. 4. 2011 Naslov: |
    |
|
|
[quote="ceps"]Zašto ne bi mogla riješiti sa supstitucijom iako je u vježbama prije supstitucije? xD Pa nije supstitucija nekakvo ''varanje'', samo način više za riješiti integral... a znam puno ljudi koji probaju sve te zadatke riješiti bez supstitucije, iako je negdje zbilja potrebna i muče se, iako će ionako ugl. sve zadatke ubuduće rješavati ili direktno iz formula ili supstitucijom ili parcijalnom integracijom ili kombinacijom navedenih.
No, bez supstitucije si na pogađanju... a ovaj integral nije teško pogoditi :) .
[latex]\int 1-sin2x dx = \int 1 dx - \int sin2x dx = x - \int sin2x dx [/latex]
A sad sa sin2x, primijeti da je [latex](cos2x)' = -2sin2x[/latex] kao i [latex](sin2x)' = 2cos2x[/latex]... ili napravi supstituciju, xD[/quote]
Naravno da nije varanje supsticutija ili parcijalna no nisam imala ideju kako to rijesiti bez supstitucije (nisam se sjetila kvadriranja). Hvala!
| ceps (napisa): | Zašto ne bi mogla riješiti sa supstitucijom iako je u vježbama prije supstitucije? xD Pa nije supstitucija nekakvo ''varanje'', samo način više za riješiti integral... a znam puno ljudi koji probaju sve te zadatke riješiti bez supstitucije, iako je negdje zbilja potrebna i muče se, iako će ionako ugl. sve zadatke ubuduće rješavati ili direktno iz formula ili supstitucijom ili parcijalnom integracijom ili kombinacijom navedenih.
No, bez supstitucije si na pogađanju... a ovaj integral nije teško pogoditi  . .
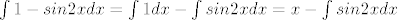
A sad sa sin2x, primijeti da je 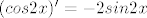 kao i kao i 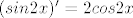 ... ili napravi supstituciju, xD ... ili napravi supstituciju, xD |
Naravno da nije varanje supsticutija ili parcijalna no nisam imala ideju kako to rijesiti bez supstitucije (nisam se sjetila kvadriranja). Hvala!
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:39 ned, 24. 4. 2011 Naslov: Postano: 17:39 ned, 24. 4. 2011 Naslov: |
    |
|
|
Čovjek me prije nekog vremena pitao mailom, pa evo, samo prenosim tadašnji odgovor. :)
[quote="ja svojedobno u mailu"]U 2.25. a), samo uvedi supstituciju [latex]t=a+b-x[/latex], pa je [latex]dt=-dx[/latex], i tu si. To pitaj ako ima nekih problema. U b), iskoristi da je [latex]\cos(x)=\sin(\pi/2-x)=\sin(\pi/2+0-x),[/latex] pa si u uvjetima a) zadatka, zar ne (s time da umjesto [latex]f[/latex] gledaš kompoziciju [latex]f[/latex] i [latex]\sin[/latex])? :) Također pitaj ako ima nekih problema.
c) je malo ružniji. Ja bih išao ovako, ali ne garantiram da nema kraćih rješenja:
Prvo podijeli taj integral na dva manja: [latex]\int_{0}^{\pi/2}xf(\sin x)dx +\int_{\pi/2}^{\pi}xf(\sin x)dx[/latex]. E, sad, prvo u ovom desnom integralu uzmi supstituciju [latex]t=\pi-x[/latex]. Dobivaš (uz [latex]\sin(\pi-t)=\sin(t)[/latex]) da zapravo tražimo sumu [latex]\int_{0}^{\pi/2}xf(\sin x)dx+\int_{0}^{\pi/2}(\pi-x)f(\sin x)dx[/latex]. Sad ih lijepo zbroji i dobivaš točno što te se tražilo. :) Hm. Zapravo, ovaj način nije zahtijevao da iskoristimo b)... u prvom načinu sam koristio to. U svakom slučaju, nadam se da nema grešaka i da je koliko-toliko smisleno jasno. :)[/quote]
Mislim, dakako, može biti da sam ja tu negdje pogriješio, sumnjivo mi je sve to. :D Možda još na kraju nije jasno, nisam raspisao: vrijedi, dakako, [latex]2\int_{0}^{\pi/2}f(\sin x)dx=\int_{0}^{\pi}f(\sin x)dx[/latex] (zapravo treba dokazati [latex]\int_{0}^{\pi/2}f(\sin x)dx=\int_{\pi/2}^{\pi}f(\sin x)dx[/latex], a to stoji uz ponovnu supstituciju [latex]t=\pi-x[/latex]). Eto, nije baš najjasnije napisano, možda je i krivo, ali što ćemo. :D Pitaj ako ima problema.
Čovjek me prije nekog vremena pitao mailom, pa evo, samo prenosim tadašnji odgovor. 
| ja svojedobno u mailu (napisa): | U 2.25. a), samo uvedi supstituciju 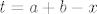 , pa je , pa je 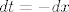 , i tu si. To pitaj ako ima nekih problema. U b), iskoristi da je , i tu si. To pitaj ako ima nekih problema. U b), iskoristi da je 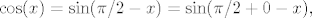 pa si u uvjetima a) zadatka, zar ne (s time da umjesto pa si u uvjetima a) zadatka, zar ne (s time da umjesto  gledaš kompoziciju gledaš kompoziciju  i i 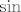 )? )?  Također pitaj ako ima nekih problema. Također pitaj ako ima nekih problema.
c) je malo ružniji. Ja bih išao ovako, ali ne garantiram da nema kraćih rješenja:
Prvo podijeli taj integral na dva manja: 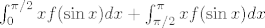 . E, sad, prvo u ovom desnom integralu uzmi supstituciju . E, sad, prvo u ovom desnom integralu uzmi supstituciju 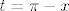 . Dobivaš (uz . Dobivaš (uz 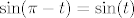 ) da zapravo tražimo sumu ) da zapravo tražimo sumu 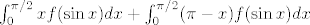 . Sad ih lijepo zbroji i dobivaš točno što te se tražilo. . Sad ih lijepo zbroji i dobivaš točno što te se tražilo.  Hm. Zapravo, ovaj način nije zahtijevao da iskoristimo b)... u prvom načinu sam koristio to. U svakom slučaju, nadam se da nema grešaka i da je koliko-toliko smisleno jasno. Hm. Zapravo, ovaj način nije zahtijevao da iskoristimo b)... u prvom načinu sam koristio to. U svakom slučaju, nadam se da nema grešaka i da je koliko-toliko smisleno jasno.  |
Mislim, dakako, može biti da sam ja tu negdje pogriješio, sumnjivo mi je sve to.  Možda još na kraju nije jasno, nisam raspisao: vrijedi, dakako, Možda još na kraju nije jasno, nisam raspisao: vrijedi, dakako, 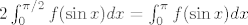 (zapravo treba dokazati (zapravo treba dokazati 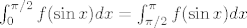 , a to stoji uz ponovnu supstituciju , a to stoji uz ponovnu supstituciju 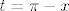 ). Eto, nije baš najjasnije napisano, možda je i krivo, ali što ćemo. ). Eto, nije baš najjasnije napisano, možda je i krivo, ali što ćemo.  Pitaj ako ima problema. Pitaj ako ima problema.
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 0:48 uto, 26. 4. 2011 Naslov: Postano: 0:48 uto, 26. 4. 2011 Naslov: |
    |
|
|
Supstitucija t = sh x pretvara integral u relativno ugodnih [latex]\frac 1 4 \operatorname{sh}^2 2t[/latex] (uz korištenje sh 2x = 2 sh x ch x), a ako uz to nekim slučajem znaš i da je ch 2x = ch^2 x + sh^2 x, iz toga slijedi i sh^2 x = (ch 2x - 1) / 2, integral čega je konačno očit. Naravno, moguće je i napisati sh^2 x samo preko eksponencijalne funkcije, pa iz toga zaključiti formulu, ili integrirati odmah eksponencijalne, ali to bi dalo prilično gadne rezultate.
Na kraju jedini problem može biti što se stvari poput u rezultatu dobivenoga sh 4y = sh (4 Arsh x) nekada smatra pristojnim raspisati, jer kada se sh 4y raspiše korištenjem formula za sinus i kosinus hiperbolni dvostrukoga kuta, dobivamo izraz koji uključuje samo sh y = sh Arsh x = x i ch y = sqrt(1 + sh^2 Arsh x) = sqrt(1+x^2), tj. nešto čisto algebarsko.
Alternativna supstitucija bi bila t = tan x, što vodi do sin^2 t / cos^5 t, što se da integrirati, ali ne vidim nenapornoga načina da se to napravi.
Ili možeš parcijalnom integracijom smanjiti stupanj x-a za jedan (što je super, jer sqrt(1 + x^2) * 2x dx ide odmah uz supstituciju t = 1 + x^2, dt = 2xdx), a integral od sqrt(1 + x^2) izračunati jednostavnijom verzijom neke od gornje dvije supstitucije ili kako već.
Naravno, ako treba ikoji od gornjih grubih opisa raspisati, napravim to :)
Supstitucija t = sh x pretvara integral u relativno ugodnih 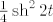 (uz korištenje sh 2x = 2 sh x ch x), a ako uz to nekim slučajem znaš i da je ch 2x = ch^2 x + sh^2 x, iz toga slijedi i sh^2 x = (ch 2x - 1) / 2, integral čega je konačno očit. Naravno, moguće je i napisati sh^2 x samo preko eksponencijalne funkcije, pa iz toga zaključiti formulu, ili integrirati odmah eksponencijalne, ali to bi dalo prilično gadne rezultate. (uz korištenje sh 2x = 2 sh x ch x), a ako uz to nekim slučajem znaš i da je ch 2x = ch^2 x + sh^2 x, iz toga slijedi i sh^2 x = (ch 2x - 1) / 2, integral čega je konačno očit. Naravno, moguće je i napisati sh^2 x samo preko eksponencijalne funkcije, pa iz toga zaključiti formulu, ili integrirati odmah eksponencijalne, ali to bi dalo prilično gadne rezultate.
Na kraju jedini problem može biti što se stvari poput u rezultatu dobivenoga sh 4y = sh (4 Arsh x) nekada smatra pristojnim raspisati, jer kada se sh 4y raspiše korištenjem formula za sinus i kosinus hiperbolni dvostrukoga kuta, dobivamo izraz koji uključuje samo sh y = sh Arsh x = x i ch y = sqrt(1 + sh^2 Arsh x) = sqrt(1+x^2), tj. nešto čisto algebarsko.
Alternativna supstitucija bi bila t = tan x, što vodi do sin^2 t / cos^5 t, što se da integrirati, ali ne vidim nenapornoga načina da se to napravi.
Ili možeš parcijalnom integracijom smanjiti stupanj x-a za jedan (što je super, jer sqrt(1 + x^2) * 2x dx ide odmah uz supstituciju t = 1 + x^2, dt = 2xdx), a integral od sqrt(1 + x^2) izračunati jednostavnijom verzijom neke od gornje dvije supstitucije ili kako već.
Naravno, ako treba ikoji od gornjih grubih opisa raspisati, napravim to 
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
rain
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (13:58:42)
Postovi: (13)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 6:18 pon, 2. 5. 2011 Naslov: Postano: 6:18 pon, 2. 5. 2011 Naslov: |
    |
|
|
2.34. b) je dosta standardan: čisto primijeti da je [latex]\displaystyle\frac{x^8-1}{x(x^8+1)}=\frac{1}{x}-2\frac{1}{x(x^8+1)}[/latex]. Budući da je [latex]\displaystyle\frac{1}{x(x^8+1)}=\frac{1}{x}-\frac{x^7}{x^8+1}[/latex], završiti nije teško, [latex]1/x[/latex] znaš integrirati, a za preostali razlomak, uzmi, naravno, supstituciju [latex]t=x^8[/latex]. :)
Što se tiče 2.35., b) dio u osnovi nije pretežak, makar tehnički ima raspisivanja. Na kraju, sve se svodi na relativno lagan, iako dosadan, račun s parcijalnim razlomcima: [latex]x^4-4x^2+4=(x^2-2)^2[/latex]. Što se tiče a) i c), trenutno mi ne pada neko lijepo rješenje (ne kažem da rješenje ne postoji, pogotovo za a), gdje bi se dalo dobiti Cardanovom formulom, ali zaboga, tko bi to radio :D) - možda će se naći netko mudar, pa nas prosvijetliti. :)
2.34. b) je dosta standardan: čisto primijeti da je 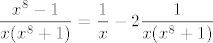 . Budući da je . Budući da je 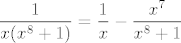 , završiti nije teško, , završiti nije teško, 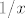 znaš integrirati, a za preostali razlomak, uzmi, naravno, supstituciju znaš integrirati, a za preostali razlomak, uzmi, naravno, supstituciju 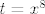 . . 
Što se tiče 2.35., b) dio u osnovi nije pretežak, makar tehnički ima raspisivanja. Na kraju, sve se svodi na relativno lagan, iako dosadan, račun s parcijalnim razlomcima: 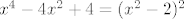 . Što se tiče a) i c), trenutno mi ne pada neko lijepo rješenje (ne kažem da rješenje ne postoji, pogotovo za a), gdje bi se dalo dobiti Cardanovom formulom, ali zaboga, tko bi to radio . Što se tiče a) i c), trenutno mi ne pada neko lijepo rješenje (ne kažem da rješenje ne postoji, pogotovo za a), gdje bi se dalo dobiti Cardanovom formulom, ali zaboga, tko bi to radio  ) - možda će se naći netko mudar, pa nas prosvijetliti. ) - možda će se naći netko mudar, pa nas prosvijetliti. 
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 13:07 sri, 4. 5. 2011 Naslov: Postano: 13:07 sri, 4. 5. 2011 Naslov: |
    |
|
|
Ja bi lijepo zamolila, iako se opet vracamo malo na pocetak, ali one sume me stvarno zbunjuju... moze li netko dati efiksano racunanje onoga, svu pricu razumijem ali onda ne znam primjeniti bas na zadatak, pa ako je netko voljan rijesiti koju sumu iz zadace, onako u detalje... Bila bih jako zahvalna.
:oops:
Ja bi lijepo zamolila, iako se opet vracamo malo na pocetak, ali one sume me stvarno zbunjuju... moze li netko dati efiksano racunanje onoga, svu pricu razumijem ali onda ne znam primjeniti bas na zadatak, pa ako je netko voljan rijesiti koju sumu iz zadace, onako u detalje... Bila bih jako zahvalna.

|
|
| [Vrh] |
|
|









