| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:49 pet, 20. 5. 2011 Naslov: Postano: 17:49 pet, 20. 5. 2011 Naslov: |
    |
|
|
Znamo da je
[latex]\ln(xy) = \ln(x) + \ln(y)[/latex]
Dakle:
[latex]1/\ln(n!)} = 1/\left(\sum_{k=1}^n \ln(k)\right) > 1 / (n \ln(n))[/latex]
Da bi suma konvergirala, sljedeci integral mora biti konacan (integralni kriterij konvergencije):
[latex]\int_1^\infty 1/(x \ln(x)) dx[/latex]
No, vrijedi:
[latex]\int 1/(x \ln(x)) dx = \ln(\ln(x)) + c[/latex]
sto ocito nije konacno na zadanom intervalu, pa red koji te zanima divergira.
Znamo da je
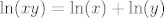
Dakle:
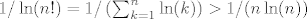
Da bi suma konvergirala, sljedeci integral mora biti konacan (integralni kriterij konvergencije):
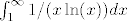
No, vrijedi:
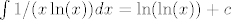
sto ocito nije konacno na zadanom intervalu, pa red koji te zanima divergira.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:49 sub, 21. 5. 2011 Naslov: Postano: 14:49 sub, 21. 5. 2011 Naslov: |
    |
|
|
Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC! :)
Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC! 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 15:48 sub, 21. 5. 2011 Naslov: Postano: 15:48 sub, 21. 5. 2011 Naslov: |
    |
|
|
[quote="frutabella"]Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC! :)[/quote]
a) Red konvergira. Raspisi si prvih nekoliko članova i primjeti sto njih povezuje.
b) Tako je, 1 je odgovor.
c) [latex]\frac{2n}{n^2 -1} \ge \frac{2n}{n^2}=\frac{2}{n} -> \infty [/latex] pa je prema teoremu o sendvicu limes jednak [latex]\infty[/latex].
d) Treba pokazati da opći član ne konvergira, pa specijalno ne konvergira u 0. To je bilo na natjecanju iz MA1. Tako da red ne konvergira.
| frutabella (napisa): | Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC!  |
a) Red konvergira. Raspisi si prvih nekoliko članova i primjeti sto njih povezuje.
b) Tako je, 1 je odgovor.
c) 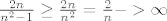 pa je prema teoremu o sendvicu limes jednak pa je prema teoremu o sendvicu limes jednak 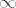 . .
d) Treba pokazati da opći član ne konvergira, pa specijalno ne konvergira u 0. To je bilo na natjecanju iz MA1. Tako da red ne konvergira.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:02 sub, 21. 5. 2011 Naslov: Postano: 18:02 sub, 21. 5. 2011 Naslov: |
    |
|
|
[quote="Tomislav"][quote="frutabella"]Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC! :)[/quote]
a) Red konvergira. Raspisi si prvih nekoliko članova i primjeti sto njih povezuje.
b) Tako je, 1 je odgovor.
c) [latex]\frac{2n}{n^2 -1} \ge \frac{2n}{n^2}=\frac{2}{n} -> \infty [/latex] pa je prema teoremu o sendvicu limes jednak [latex]\infty[/latex].
d) Treba pokazati da opći član ne konvergira, pa specijalno ne konvergira u 0. To je bilo na natjecanju iz MA1. Tako da red ne konvergira.[/quote]
Ovako:
a) zakljucila sam da bi limes suma za neparan i paran n trbao biti 0, ali opet nisam bas sasvim sigurna... :S
c) ne razumijem kako to ide u besk, zar nije 2*(1/n) ----> kada n ide u besk, zar nije to onda 0 ?
d) ako mozes malo raspisati bila bih jako zahvalna...
Sve mi se nesto pomijesalo, limes suma, limes , limes i samo limes...
| Tomislav (napisa): | | frutabella (napisa): | Moze pomoc, odnosno provjera za 3.2. :
Pod a) mislim da red divergira, 2 razlicita gomilista.
b) 1
c) Hm, kad rastavim na parcijalne sume, ispadne mi A=1 i B=1, sto znaci da se sume ne mogu pokratiti, sta da onda radim ? (kad bi se dale kratiti, ispalo bi rjesenje 1/2).
d) HITNA POMOC!  |
a) Red konvergira. Raspisi si prvih nekoliko članova i primjeti sto njih povezuje.
b) Tako je, 1 je odgovor.
c) 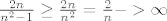 pa je prema teoremu o sendvicu limes jednak pa je prema teoremu o sendvicu limes jednak 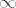 . .
d) Treba pokazati da opći član ne konvergira, pa specijalno ne konvergira u 0. To je bilo na natjecanju iz MA1. Tako da red ne konvergira. |
Ovako:
a) zakljucila sam da bi limes suma za neparan i paran n trbao biti 0, ali opet nisam bas sasvim sigurna... :S
c) ne razumijem kako to ide u besk, zar nije 2*(1/n) ----> kada n ide u besk, zar nije to onda 0 ?
d) ako mozes malo raspisati bila bih jako zahvalna...
Sve mi se nesto pomijesalo, limes suma, limes , limes i samo limes...
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 18:37 sub, 21. 5. 2011 Naslov: Postano: 18:37 sub, 21. 5. 2011 Naslov: |
    |
|
|
Znaci ovako:
a) To je geometrijski red. Ubaci a_1 i q u formulu i dobijes limes je 2/3 ako se ne varam.
c) suma k=1 do infinity od (1/k) je manja od pocetne sume.
A suma k=1 do infinity od (1/k) ide u beskonacno, znaci da je originalna suma > beskonacno, pa mora i pocetni limes biti beskonacno.
d) Dokaz nije bas najkraci, pa cu napisati samo ideju. Znaci pretpostavi da za neki alfa razlicit od 0 sin(alfa*n) konvergira u L. Tada i sin(alfa*(n+1)) ide u L, a 0=lim (sin(alfa*(n+2))-sin(alfa*n))=sada iskoristis formulu (sinx-siny)=(sad nisam siguran tocno, ali nesto ovog tipa)=+-2cos(alfa)*cos((n+1)alfa->lim (cos(n+1)alfa)=0, pa je i lim cos(nalfa)=0, tj 0=lim (cos(n+2)alfa)-cos(n*alfa)=sad formula za cosx-cosy=(sada dode nesto slicno ovome)=+-2sin(alfa)sin((n+1)alfa)=0, -> lim sin((n+1)alfa)=0, tj lim (sin((n+1)alfa))^2=0. A odprije imamo lim (cos((n+1)alfa))^2=0, ali (sinx)^2 +(cos(x))^2=1, kontradikcija. Ako netko tko je bio na natjecanju (i rijesio ovaj zadatak) zeli ovo lijepo napisati u latexu, slobodno.. jer sam ja pomalo lijen. :D
Znaci ovako:
a) To je geometrijski red. Ubaci a_1 i q u formulu i dobijes limes je 2/3 ako se ne varam.
c) suma k=1 do infinity od (1/k) je manja od pocetne sume.
A suma k=1 do infinity od (1/k) ide u beskonacno, znaci da je originalna suma > beskonacno, pa mora i pocetni limes biti beskonacno.
d) Dokaz nije bas najkraci, pa cu napisati samo ideju. Znaci pretpostavi da za neki alfa razlicit od 0 sin(alfa*n) konvergira u L. Tada i sin(alfa*(n+1)) ide u L, a 0=lim (sin(alfa*(n+2))-sin(alfa*n))=sada iskoristis formulu (sinx-siny)=(sad nisam siguran tocno, ali nesto ovog tipa)=+-2cos(alfa)*cos((n+1)alfa->lim (cos(n+1)alfa)=0, pa je i lim cos(nalfa)=0, tj 0=lim (cos(n+2)alfa)-cos(n*alfa)=sad formula za cosx-cosy=(sada dode nesto slicno ovome)=+-2sin(alfa)sin((n+1)alfa)=0, -> lim sin((n+1)alfa)=0, tj lim (sin((n+1)alfa))^2=0. A odprije imamo lim (cos((n+1)alfa))^2=0, ali (sinx)^2 +(cos(x))^2=1, kontradikcija. Ako netko tko je bio na natjecanju (i rijesio ovaj zadatak) zeli ovo lijepo napisati u latexu, slobodno.. jer sam ja pomalo lijen. 
|
|
| [Vrh] |
|
sagi
Forumaš(ica)

Pridružen/a: 30. 10. 2010. (14:46:39)
Postovi: (16)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:53 sri, 25. 5. 2011 Naslov: Postano: 10:53 sri, 25. 5. 2011 Naslov: |
    |
|
|
Zadatak nije težak, pa evo par generalnih uputa. Ako bude problema, pitaj.
Dakle, primijeti da su svi članovi pozitivni, pa ako ograničimo ovaj red odozgo nekim drugim konvergentnim redom, gotovi smo.
E, a sad pokaži da je (za dovoljno velike [latex]k[/latex]) [latex]\displaystyle\frac{\ln(k)}{k-1}\leq\frac{1}{\sqrt{k}}[/latex] (to je dosta standardan trik kad se želiš riješiti [latex]\ln[/latex]-ova - zamijeni ih nečime što će ti se svesti na stvar oblika [latex]1/n^p[/latex]). To možeš dokazati kako te već veseli... L'Hôpitalovim pravilom, supstitucijom [latex]t=\ln k[/latex] ili kako već hoćeš. :)
Sad smo gotovi: naime, (nakon konačno mnogo članova, ali ovi prije nam ionako ne igraju ulogu za konvergenciju) vrijedi [latex]\displaystyle\frac{\ln(k)}{k-1}\leq\frac{1}{k\sqrt{k}}[/latex]. Budući da suma reda zadana članovima zdesna konvergira (to ste dokazivali - radi se o sumi oblika [latex]\displaystyle\sum\frac{1}{(n^(3/2)}[/latex], gotovi smo.
To je to. :)
Zadatak nije težak, pa evo par generalnih uputa. Ako bude problema, pitaj.
Dakle, primijeti da su svi članovi pozitivni, pa ako ograničimo ovaj red odozgo nekim drugim konvergentnim redom, gotovi smo.
E, a sad pokaži da je (za dovoljno velike  ) ) 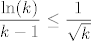 (to je dosta standardan trik kad se želiš riješiti (to je dosta standardan trik kad se želiš riješiti 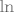 -ova - zamijeni ih nečime što će ti se svesti na stvar oblika -ova - zamijeni ih nečime što će ti se svesti na stvar oblika 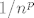 ). To možeš dokazati kako te već veseli... L'Hôpitalovim pravilom, supstitucijom ). To možeš dokazati kako te već veseli... L'Hôpitalovim pravilom, supstitucijom 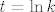 ili kako već hoćeš. ili kako već hoćeš. 
Sad smo gotovi: naime, (nakon konačno mnogo članova, ali ovi prije nam ionako ne igraju ulogu za konvergenciju) vrijedi 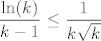 . Budući da suma reda zadana članovima zdesna konvergira (to ste dokazivali - radi se o sumi oblika . Budući da suma reda zadana članovima zdesna konvergira (to ste dokazivali - radi se o sumi oblika 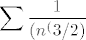 , gotovi smo. , gotovi smo.
To je to. 
|
|
| [Vrh] |
|
sagi
Forumaš(ica)

Pridružen/a: 30. 10. 2010. (14:46:39)
Postovi: (16)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
|












