| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:28 čet, 2. 6. 2011 Naslov: Postano: 14:28 čet, 2. 6. 2011 Naslov: |
    |
|
|
Evo jedan banalan zadacic, a koji me malo zbunjuje...
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.11, pod c)
Meni je tu prvo naumpalo da ga odozgo ogranicim s 1/n > an, sto vrijedi,
( n*2^n > n ), a pri tom znam da je to harmonijski red i on divergira, no u rjesenjima su ogranicili s 1/2^n gdje taj red konvergira...
:S :roll:
i pod f) :
zasto vrijedi lim (arctg(2^-1))/(2^-1)=1 ?
Evo jedan banalan zadacic, a koji me malo zbunjuje...
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.11, pod c)
Meni je tu prvo naumpalo da ga odozgo ogranicim s 1/n > an, sto vrijedi,
( n*2^n > n ), a pri tom znam da je to harmonijski red i on divergira, no u rjesenjima su ogranicili s 1/2^n gdje taj red konvergira...
:S 
i pod f) :
zasto vrijedi lim (arctg(2^-1))/(2^-1)=1 ?
Zadnja promjena: frutabella; 14:35 čet, 2. 6. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 14:34 čet, 2. 6. 2011 Naslov: Postano: 14:34 čet, 2. 6. 2011 Naslov: |
    |
|
|
[quote="frutabella"]Evo jedan banalan zadacic, a koji me malo zbunjuje...
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.11, pod c)
Meni je tu prvo naumpalo da ga odozgo ogranicim s 1/n > an, sto vrijedi,
( n*2^n > n ), a pri tom znam da je to harmonijski red i on divergira, no u rjesenjima su ogranicili s 1/2^n gdje taj red konvergira...
:S :roll:[/quote]
Da, i gdje je problem? Svaki se red može odozgo ograničiti s nekim divergirajućim (npr. sa [latex]2^n[/latex]). Dakle to što je red manji od divergirajućeg [latex]1/n[/latex], ne znači ništa.
[quote="frutabella"]
i pod f) :
zasto vrijedi lim (arctg(2^-n))/(2^-n)=1 ?[/quote]
Zato što [latex]2^{-n}[/latex] teži u 0 (to možeš supstituirati), i sada budući da [latex]\frac{x}{\tan x}\to 1[/latex] kad [latex]x\to 0[/latex] (to je poznato iz prvog semestra, a nije ni problem dokazati), onda i [latex]\frac{\arctan t}{t}\to 1[/latex] kad [latex]t\to 0[/latex].
| frutabella (napisa): | Evo jedan banalan zadacic, a koji me malo zbunjuje...
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.11, pod c)
Meni je tu prvo naumpalo da ga odozgo ogranicim s 1/n > an, sto vrijedi,
( n*2^n > n ), a pri tom znam da je to harmonijski red i on divergira, no u rjesenjima su ogranicili s 1/2^n gdje taj red konvergira...
:S  |
Da, i gdje je problem? Svaki se red može odozgo ograničiti s nekim divergirajućim (npr. sa 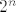 ). Dakle to što je red manji od divergirajućeg ). Dakle to što je red manji od divergirajućeg 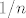 , ne znači ništa. , ne znači ništa.
| frutabella (napisa): |
i pod f) :
zasto vrijedi lim (arctg(2^-n))/(2^-n)=1 ? |
Zato što 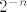 teži u 0 (to možeš supstituirati), i sada budući da teži u 0 (to možeš supstituirati), i sada budući da 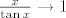 kad kad 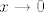 (to je poznato iz prvog semestra, a nije ni problem dokazati), onda i (to je poznato iz prvog semestra, a nije ni problem dokazati), onda i 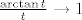 kad kad 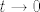 . .
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 18:00 čet, 2. 6. 2011 Naslov: Postano: 18:00 čet, 2. 6. 2011 Naslov: |
    |
|
|
Za f) mislim da bi D'Alambertov kriterij trebao proći i pokazati da konvergira, ovako napamet.
EDIT: A i za g), kada gledaš D'Alambertov kriterij, [latex]\frac{a_{n+1}}{a_n} = \sqrt{2} - \sqrt[2n+3]{2} [/latex], a i sama si maloprije pisala taj limes za n-ti korijen od a>0, pa mislim da ti ne trebam dalje pomagat. :D
Za f) mislim da bi D'Alambertov kriterij trebao proći i pokazati da konvergira, ovako napamet.
EDIT: A i za g), kada gledaš D'Alambertov kriterij, 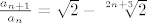 , a i sama si maloprije pisala taj limes za n-ti korijen od a>0, pa mislim da ti ne trebam dalje pomagat. , a i sama si maloprije pisala taj limes za n-ti korijen od a>0, pa mislim da ti ne trebam dalje pomagat. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:09 čet, 2. 6. 2011 Naslov: Postano: 18:09 čet, 2. 6. 2011 Naslov: |
    |
|
|
[quote="ceps"]Za f) mislim da bi D'Alambertov kriterij trebao proći i pokazati da konvergira, ovako napamet.[/quote]
Da, vrlo vjerojatno da DK, pa ispadne
a / (1+a^[n+1] ) ----- n ide u besk -----> 0 < 1 , pa red konvergira
Nadam se da ne grijesim.
Ovaj pod g), ispada dobro.
Bit ce da sam se prepala silnih korijena i produkata. :D :D :D :D
HVALA CEPS!
| ceps (napisa): | | Za f) mislim da bi D'Alambertov kriterij trebao proći i pokazati da konvergira, ovako napamet. |
Da, vrlo vjerojatno da DK, pa ispadne
a / (1+a^[n+1] ) ----- n ide u besk -----> 0 < 1 , pa red konvergira
Nadam se da ne grijesim.
Ovaj pod g), ispada dobro.
Bit ce da sam se prepala silnih korijena i produkata.    
HVALA CEPS!
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 12:15 pet, 3. 6. 2011 Naslov: Postano: 12:15 pet, 3. 6. 2011 Naslov: |
    |
|
|
[quote="frutabella"]Pitanje:
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.14:
a) da li je dovoljno i ispravno ograniciti ga odozdo samo sa (1/2)^n
b) da li je ispravno gledati kao umnozak 1/nln(n) * 1/ln(lnn), i dokazati da prvi faktor divergira pa to onda povlaci da sve divergira?
d) tipican je primjer usporednog kriterija zbog ( n! < n^n), a da li se mozei Dalamberovim kriterijem (zanima me zbog ln-a) , i dođemo do dijela
1/ln(n+1) i onda idemo njega uspoređiovati s > 1/ lnn > 1/n
e) molim pomoc! :)
f) mogu usporedit odozdo s n^2 / n^n ( a ovo konvergira u 0) pa onda sve konvergira?
g) nuzan uvjet nije zadovoljen.[/quote]
a) Nije mi bas jasno kako si dosla do 1/2^n hmm..mozes npr staviti n/2^n, a to se lako pokaze da konvergira.
b) Tako ne mozes, zato jer bi prema tome onda takodjer bilo 1/n^2=1/n * 1/n. Posto 1/n divergira onda sve divergira, a 1/n^2 ne divergira.
d) Pogledaj 1. stranicu, negdje 2-3 post (vsego), tamo je rjesenje.
e) Fuj :S
f) Ako bis to napravila, onda imas lim n->inf (n/ln(n))^n sto ide u inf. Zato bolje iskoristi Cauchy-jev kriterij.
g) Yep.
| frutabella (napisa): | Pitanje:
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.14:
a) da li je dovoljno i ispravno ograniciti ga odozdo samo sa (1/2)^n
b) da li je ispravno gledati kao umnozak 1/nln(n) * 1/ln(lnn), i dokazati da prvi faktor divergira pa to onda povlaci da sve divergira?
d) tipican je primjer usporednog kriterija zbog ( n! < n^n), a da li se mozei Dalamberovim kriterijem (zanima me zbog ln-a) , i dođemo do dijela
1/ln(n+1) i onda idemo njega uspoređiovati s > 1/ lnn > 1/n
e) molim pomoc! 
f) mogu usporedit odozdo s n^2 / n^n ( a ovo konvergira u 0) pa onda sve konvergira?
g) nuzan uvjet nije zadovoljen. |
a) Nije mi bas jasno kako si dosla do 1/2^n hmm..mozes npr staviti n/2^n, a to se lako pokaze da konvergira.
b) Tako ne mozes, zato jer bi prema tome onda takodjer bilo 1/n^2=1/n * 1/n. Posto 1/n divergira onda sve divergira, a 1/n^2 ne divergira.
d) Pogledaj 1. stranicu, negdje 2-3 post (vsego), tamo je rjesenje.
e) Fuj :S
f) Ako bis to napravila, onda imas lim n→inf (n/ln(n))^n sto ide u inf. Zato bolje iskoristi Cauchy-jev kriterij.
g) Yep.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 12:35 pet, 3. 6. 2011 Naslov: Postano: 12:35 pet, 3. 6. 2011 Naslov: |
    |
|
|
[quote="Tomislav"][quote="frutabella"]Pitanje:
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.14:
a) da li je dovoljno i ispravno ograniciti ga odozdo samo sa (1/2)^n
b) da li je ispravno gledati kao umnozak 1/nln(n) * 1/ln(lnn), i dokazati da prvi faktor divergira pa to onda povlaci da sve divergira?
d) tipican je primjer usporednog kriterija zbog ( n! < n^n), a da li se mozei Dalamberovim kriterijem (zanima me zbog ln-a) , i dođemo do dijela
1/ln(n+1) i onda idemo njega uspoređiovati s > 1/ lnn > 1/n
e) molim pomoc! :)
f) mogu usporedit odozdo s n^2 / n^n ( a ovo konvergira u 0) pa onda sve konvergira?
g) nuzan uvjet nije zadovoljen.[/quote]
a) Nije mi bas jasno kako si dosla do 1/2^n hmm..mozes npr staviti n/2^n, a to se lako pokaze da konvergira.
b) Tako ne mozes, zato jer bi prema tome onda takodjer bilo 1/n^2=1/n * 1/n. Posto 1/n divergira onda sve divergira, a 1/n^2 ne divergira.
d) Pogledaj 1. stranicu, negdje 2-3 post (vsego), tamo je rjesenje.
e) Fuj :S
f) Ako bis to napravila, onda imas lim n->inf (n/ln(n))^n sto ide u inf. Zato bolje iskoristi Cauchy-jev kriterij.
g) Yep.[/quote]
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga... :D :D :D
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0. :D
| Tomislav (napisa): | | frutabella (napisa): | Pitanje:
http://web.math.hr/nastava/analiza/files/ch3_2.pdf
zad 3.14:
a) da li je dovoljno i ispravno ograniciti ga odozdo samo sa (1/2)^n
b) da li je ispravno gledati kao umnozak 1/nln(n) * 1/ln(lnn), i dokazati da prvi faktor divergira pa to onda povlaci da sve divergira?
d) tipican je primjer usporednog kriterija zbog ( n! < n^n), a da li se mozei Dalamberovim kriterijem (zanima me zbog ln-a) , i dođemo do dijela
1/ln(n+1) i onda idemo njega uspoređiovati s > 1/ lnn > 1/n
e) molim pomoc! 
f) mogu usporedit odozdo s n^2 / n^n ( a ovo konvergira u 0) pa onda sve konvergira?
g) nuzan uvjet nije zadovoljen. |
a) Nije mi bas jasno kako si dosla do 1/2^n hmm..mozes npr staviti n/2^n, a to se lako pokaze da konvergira.
b) Tako ne mozes, zato jer bi prema tome onda takodjer bilo 1/n^2=1/n * 1/n. Posto 1/n divergira onda sve divergira, a 1/n^2 ne divergira.
d) Pogledaj 1. stranicu, negdje 2-3 post (vsego), tamo je rjesenje.
e) Fuj :S
f) Ako bis to napravila, onda imas lim n→inf (n/ln(n))^n sto ide u inf. Zato bolje iskoristi Cauchy-jev kriterij.
g) Yep. |
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga...   
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0. 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 12:52 pet, 3. 6. 2011 Naslov: Postano: 12:52 pet, 3. 6. 2011 Naslov: |
    |
|
|
[quote="frutabella"]
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga... :D :D :D
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0. :D[/quote]
a) Dobro, ali sto si postigla time da si pokazala da je pocetna suma >neke konacne?
b) Kao sto je ceps rekao, koristi integralni kriterij.
f) Ako pokazes to sto zelis, samo si pokazala da je opet suma >neke sume ciji je limes opceg clana jednak 0.. a sto ti to znaci? :wink:
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
Slight offtopic: Bas gledam zadatke iz redova s prijasnjih kolokvija, i svaki 2-3 mi se cini uzasno tezak, npr 3.a) proslogodisnji...za njega imam rješenje, ali je za doci do njega trebalo puuuno vremena, koje nemam na kolokviju, tako da kao da ga nisam ni rijesio. Ima li netko neko "jednostavno" rjesenje za taj zadatak? Takodjer ja i kolega nismo uspjeli pokazati da je niz [latex]a_n=\frac{arctg(n!)}{n}[/latex] strogo padajuc, pa ako netko to zna, neka napise.
| frutabella (napisa): |
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga...   
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0.  |
a) Dobro, ali sto si postigla time da si pokazala da je pocetna suma >neke konacne?
b) Kao sto je ceps rekao, koristi integralni kriterij.
f) Ako pokazes to sto zelis, samo si pokazala da je opet suma >neke sume ciji je limes opceg clana jednak 0.. a sto ti to znaci? 
Added after 11 minutes:
Slight offtopic: Bas gledam zadatke iz redova s prijasnjih kolokvija, i svaki 2-3 mi se cini uzasno tezak, npr 3.a) proslogodisnji...za njega imam rješenje, ali je za doci do njega trebalo puuuno vremena, koje nemam na kolokviju, tako da kao da ga nisam ni rijesio. Ima li netko neko "jednostavno" rjesenje za taj zadatak? Takodjer ja i kolega nismo uspjeli pokazati da je niz 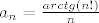 strogo padajuc, pa ako netko to zna, neka napise. strogo padajuc, pa ako netko to zna, neka napise.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 12:53 pet, 3. 6. 2011 Naslov: Postano: 12:53 pet, 3. 6. 2011 Naslov: |
    |
|
|
[quote="Tomislav"][quote="frutabella"]
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga... :D :D :D
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0. :D[/quote]
a) Dobro, ali sto si postigla time da si pokazala da je pocetna suma >neke konacne?
b) Kao sto je ceps rekao, koristi integralni kriterij.
f) Ako pokazes to sto zelis, samo si pokazala da je opet suma >neke sume ciji je limes opceg clana jednak 0.. a sto ti to znaci? :wink:[/quote]
a) pa ta konacna suma konvergira (geometrijski red) pa onda i pocetni red konvergira, zar ne? :S
b) OK
c) pa ako je limes 0, znaci limes postoji pa taj red konvergira -----> pa onda i pocetni...
Plasi me da nesto ne konatm bas... :(
| Tomislav (napisa): | | frutabella (napisa): |
a) Dosla sam do (1/2)^n, pa lijepo... nazvinik sam ostavila na miru, a za brojnik sam zakljucila da je 1 sigurno manje od onog tamo n* cos (bla, bla)
b) i sta ona savjetujes kako rjesit?
e) ako je tebi fuj, onda se uopce ne moram trudi oko toga...   
f) Mislim da me nisi tu bas razumio,
naime, znamo da vrijedi ln(n) < n, pa je onda n^2/[ln(n)]^n > n^2/n^n ,
i onda ovo zadnje ide u 0.  |
a) Dobro, ali sto si postigla time da si pokazala da je pocetna suma >neke konacne?
b) Kao sto je ceps rekao, koristi integralni kriterij.
f) Ako pokazes to sto zelis, samo si pokazala da je opet suma >neke sume ciji je limes opceg clana jednak 0.. a sto ti to znaci?  |
a) pa ta konacna suma konvergira (geometrijski red) pa onda i pocetni red konvergira, zar ne? :S
b) OK
c) pa ako je limes 0, znaci limes postoji pa taj red konvergira -----> pa onda i pocetni...
Plasi me da nesto ne konatm bas... 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 12:58 pet, 3. 6. 2011 Naslov: Postano: 12:58 pet, 3. 6. 2011 Naslov: |
    |
|
|
Malo si pobrkala < i > :).
Znaci ovako, ako je s1 suma jednog niza i s2 suma nekog drugog.
Ja znam da je s2>s1. Ako s1 konvergira, to ne znaci da s2 konvergira. Npr s1=1/n^2, s2=1/n.
Znaci ovo je ispravno: Ako je s2>s1 i s2 konvergira, onda konvergira i s1 (uz uvjet da oba evo npr imaju pozitivne clanove).
Ako s2>s1 i s1 divergira (poz clanovi), onda s2 takodjer divergira. Ovo sto sam napisao sad primjeni na te zadatke :)
Malo si pobrkala < i >  . .
Znaci ovako, ako je s1 suma jednog niza i s2 suma nekog drugog.
Ja znam da je s2>s1. Ako s1 konvergira, to ne znaci da s2 konvergira. Npr s1=1/n^2, s2=1/n.
Znaci ovo je ispravno: Ako je s2>s1 i s2 konvergira, onda konvergira i s1 (uz uvjet da oba evo npr imaju pozitivne clanove).
Ako s2>s1 i s1 divergira (poz clanovi), onda s2 takodjer divergira. Ovo sto sam napisao sad primjeni na te zadatke 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 13:46 pet, 3. 6. 2011 Naslov: Postano: 13:46 pet, 3. 6. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Malo si pobrkala < i > :).
Znaci ovako, ako je s1 suma jednog niza i s2 suma nekog drugog.
Ja znam da je s2>s1. Ako s1 konvergira, to ne znaci da s2 konvergira. Npr s1=1/n^2, s2=1/n.
Znaci ovo je ispravno: Ako je s2>s1 i s2 konvergira, onda konvergira i s1 (uz uvjet da oba evo npr imaju pozitivne clanove).
Ako s2>s1 i s1 divergira (poz clanovi), onda s2 takodjer divergira. Ovo sto sam napisao sad primjeni na te zadatke :)[/quote]
E super, lijepo si to objasnio, hvala na strpljivosti. :D procitala sam to milion puta, al sve mi se pobrkalo... :oops:
e sad zad 3.15:
a) tu imamo dva gomilista 1 i -1, pa red divergira ?
b) Po LK red konvergira, ali po mom skromnom sudu, apsolutno ne konvergira, suma ide u +besk
c) opet prema LK konvergira, ali apsolutno divergira
d) hmm, ovdje bi trebao ici usproedni kriterij, no ne znam da li bas vrijedi da je 1/n manji od zadanog reda... jer kad bi bio onda bi divergirao... (ma da se pita uvjetna i aps konvergencija, pa mozda divergenicja ovdje ne dolazi u obzir... :S )
e) HELP!
| Tomislav (napisa): | Malo si pobrkala < i >  . .
Znaci ovako, ako je s1 suma jednog niza i s2 suma nekog drugog.
Ja znam da je s2>s1. Ako s1 konvergira, to ne znaci da s2 konvergira. Npr s1=1/n^2, s2=1/n.
Znaci ovo je ispravno: Ako je s2>s1 i s2 konvergira, onda konvergira i s1 (uz uvjet da oba evo npr imaju pozitivne clanove).
Ako s2>s1 i s1 divergira (poz clanovi), onda s2 takodjer divergira. Ovo sto sam napisao sad primjeni na te zadatke  |
E super, lijepo si to objasnio, hvala na strpljivosti.  procitala sam to milion puta, al sve mi se pobrkalo... procitala sam to milion puta, al sve mi se pobrkalo... 
e sad zad 3.15:
a) tu imamo dva gomilista 1 i -1, pa red divergira ?
b) Po LK red konvergira, ali po mom skromnom sudu, apsolutno ne konvergira, suma ide u +besk
c) opet prema LK konvergira, ali apsolutno divergira
d) hmm, ovdje bi trebao ici usproedni kriterij, no ne znam da li bas vrijedi da je 1/n manji od zadanog reda... jer kad bi bio onda bi divergirao... (ma da se pita uvjetna i aps konvergencija, pa mozda divergenicja ovdje ne dolazi u obzir... :S )
e) HELP!
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 13:55 pet, 3. 6. 2011 Naslov: Postano: 13:55 pet, 3. 6. 2011 Naslov: |
    |
|
|
e)
Za sin x općenito znaš da je [latex]\in [-1, 1][/latex]... Pa zato ovaj sinus u sinusu može maksimalno biti [latex]sin(sin 1)[/latex], a broj sin(1) je manji od 1...
Ako ti treba još što, samo reci... ovo je jedan ''blagi'' hint koji možda pomogne. :D
d)
Ispiši si prvih par članova reda, pa ti možda sine. :D [latex]cos \frac{n\pi}{2}[/latex] i ne daje baš puno različitih vrijednosti... ili je 0, ili 1 ili -1... tako da ovaj red možeš puno jednostavnije zapisati.
e)
Za sin x općenito znaš da je 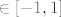 ... Pa zato ovaj sinus u sinusu može maksimalno biti ... Pa zato ovaj sinus u sinusu može maksimalno biti 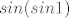 , a broj sin(1) je manji od 1... , a broj sin(1) je manji od 1...
Ako ti treba još što, samo reci... ovo je jedan ''blagi'' hint koji možda pomogne. 
d)
Ispiši si prvih par članova reda, pa ti možda sine.  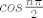 i ne daje baš puno različitih vrijednosti... ili je 0, ili 1 ili -1... tako da ovaj red možeš puno jednostavnije zapisati. i ne daje baš puno različitih vrijednosti... ili je 0, ili 1 ili -1... tako da ovaj red možeš puno jednostavnije zapisati.
|
|
| [Vrh] |
|
|









