|
Dakle:
3. a) Zadana je matrica operatora [latex]A = \begin{bmatrix}
\frac{4}{3} & \frac{2}{3} \\
\frac{1}{3} & \frac{5}{3} \\
\end{bmatrix}[/latex] u istom paru baza. Neka je [latex]e= \left\{ e_{1}=a_{1}t+b_{1},e_{2}=a_{2}t+b_{2} \right\}[/latex] zadana baza.
Uočimo: [latex]Ae_{1}=t(a_{1}t+b_{1})'+a_{1}t+b_{1}=2a_{1}t+b_{1}[/latex]. Analogno, [latex]Ae_{2}=2a_{2}t+b_{2}[/latex].
Po matrici znamo: [latex]Ae_{1}=\frac{4}{3}(a_{1}t+b_{1})+\frac{1}{3}(a_{2}t+b_{2})[/latex], [latex]Ae_{2}=\frac{2}{3}(a_{1}t+b_{1})+\frac{5}{3}(a_{2}t+b_{2})[/latex]. Sada uvrstimo čemu je to jednako i, s obzirom da je {1, t} baza (odnosno linearno nezavisan skup) prostora [latex]P_{1}[/latex], dobivamo jednadžbe:
[latex]6a_{1}=4a_{1}+a_{2}[/latex]
[latex]6a_{2}=2a_{1}+5a_{2}[/latex]
[latex]3b_{1}=4b_{1}+b_{2}[/latex]
[latex]3b_{2}=2b_{1}+5b_{2}[/latex]
Rješenja tog sustava su [latex]2a_{1}=a_{2}[/latex], [latex]b_{1}=-b_{2}[/latex]. Dakle, baza u zadanoj matrici je bilo koja matrica oblika [latex]\left\{ a_{1}t+2a_{1},-b_{2}t+b_{2} \right\}[/latex]. (Možete uvrstiti i konkretne brojeve za [latex]a_{1}[/latex] i [latex]b_{2}[/latex], nije greška.)
b) Može se riješiti analogno kao i a) zadatak (pa doći u nekakvu kontradikciju, npr. skup polinoma koji ne bi mogao biti baza vektorskog prostora), ali postoji i jedan brži trik: poznato je da su sve matrice istog operatora u bilo kojim bazama slične (odnosno, jedna se može dobiti preko druge množeći je slijeva ili zdesna; konkretno: [latex][A]_{f'}^{e'}=[I]_{f'}^{f}[A]_{f}^{e}[I]_{e}^{e'}[/latex]). Posebno, zadana matrica je slična matrici istog operatora zapisanoj u kanonskom paru baza.
E sada, znamo kako djeluje operator. Dakle, izračunamo [latex]A(1)[/latex], [latex]A(t)[/latex], [latex]A(t^2)[/latex] i [latex]A(t^3)[/latex] i raspišemo ga preko baze [latex]{1, t, t^2, t^3}[/latex].
Spominjali smo kako slične matrice imaju neka "zanimljiva, ista svojstva". Primjerice, jednake determinante (što se lako pokaže, a i radilo se na faksu). Sada izračunamo determinante ovih dviju matrica (koje bi trebale biti jednake) i, ako dobijemo da su različite, znamo da zadana matrica nije slična matrici za koju znamo da pripada operatoru - što ujedno znači i da ta matrica nije zapis operatora u nikojem paru baza.
4. Zadatak nije baš šablonski, a ja nemam tekst zadatka, pa ću pokušati iz glave, koliko se sjećam... :oops:
Dakle, recimo da je bio zadan operator [latex]A(p)(t)=(tp(t-2))''[/latex]. Operator možemo raspisati tako da napravimo prvu i drugu derivaciju umnoška (i zbroja) polinoma ([latex]A(p)(t)=2p'(t-2)+tp''(t-2)[/latex], ako se ne varam). Sada možemo raspisati [latex]p(t)=\sum_{i=0}^{n}a_{i}t^{i}[/latex], izračunati [latex]p'(t)[/latex] i [latex]p''(t)[/latex] te to uvrstiti u gornju jednakost.
Slično kao i na vježbama, kada tražimo jezgru, pretpostavit ćemo da je [latex]p \in Ker(A)[/latex], a za sliku ćemo raspisati [latex]A(p)[/latex] preko nekog sustava izvodnica za [latex]P_{n}[/latex] (pa onda, po potrebi, reducirati do baze).
E sada, da budem sasvim iskren, malo se žurim, pa ne stignem točno raspisati što se na kraju dobije ( :oops: ), ali se nadam da nije problem ako odmah napišem svoj rezultat (ako je, uz to, dobro raspisan; ali ovako otprilike ide):
[latex]A(p)(t)=2a_{1}+\sum_{i=2}^{n}[ia_{i}(2t+i-5)(t-2)^{i-2}][/latex].
Što sada?
No, uočimo: svaki član sume, kada se raspiše, je polinom [latex]i-1.[/latex] stupnja, odnosno stupnjevi idu od [latex]1[/latex] do [latex]n-1[/latex] (i vodeći koeficijent je neskrativ). [latex]2a_{1}[/latex] predstavlja slobodni član, stoga je ovo raspis polinoma [latex]n-1.[/latex] stupnja.
Dakle:
1) Ako tražimo jezgru, rješavamo jednadžbu [latex]A(p)(t)=0[/latex]. Ako formiramo skup koji se sastoji od polinoma koji su članovi ove sume (i pridodamo još konstantni polinom), tj. [latex]\left\{ 1, 2t+2-5, (2t+3-5)(t-2), ..., (2t+n-5)(t-2)^{n-2} \right\}[/latex], uočavamo da je to linearno nezavisan skup jer se nijedan element toga skupa ne može prikazati preko svoga prethodnika (svaki član skupa je većeg stupnja od bilo kojeg prethodnog). Stoga su i svi koeficijenti ispred tih elemenata jednaki nuli, tj.: [latex]2a_{1}=0[/latex], [latex]2a_{2}=0[/latex], [latex]3a_{3}=0[/latex], ..., [latex]na_{n}=0[/latex], iz čega proizlazi [latex]a_{1}=a_{2}=...=a_{n}=0[/latex]. Dakle, jezgri pripadaju svi polinomi oblika [latex]p(t)=a_{0}[/latex], odnosno konstantni polinomi. [latex]Ker(A)=[\left\{ 1 \right\}][/latex], [latex]d(A)=1[/latex].
2) Opet, gornji zapis je zapravo raspis po linearno nezavisnom skupu [latex]\left\{ 1, 2t+2-5, (2t+3-5)(t-2), ..., (2t+n-5)(t-2)^{n-2} \right\}[/latex] koji je stoga i skup izvodnica za sliku, pa je to baza za [latex]Im(A)[/latex]. Elemenata ima [latex]n-1[/latex] i to su polinomi od [latex]0.[/latex] do [latex]n-1.[/latex] stupnja, dakle [latex]Im(A)=P_{n-1}[/latex], [latex]r(A)=n[/latex].
(Uočimo da nam rješenja zadovoljavaju teorem o rangu i defektu.)
Dakle:
3. a) Zadana je matrica operatora 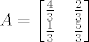 u istom paru baza. Neka je u istom paru baza. Neka je 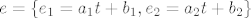 zadana baza. zadana baza.
Uočimo: 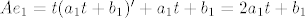 . Analogno, . Analogno, 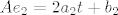 . .
Po matrici znamo: 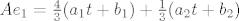 , , 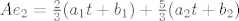 . Sada uvrstimo čemu je to jednako i, s obzirom da je {1, t} baza (odnosno linearno nezavisan skup) prostora . Sada uvrstimo čemu je to jednako i, s obzirom da je {1, t} baza (odnosno linearno nezavisan skup) prostora 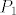 , dobivamo jednadžbe: , dobivamo jednadžbe:
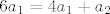
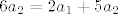
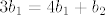
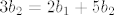
Rješenja tog sustava su 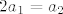 , , 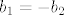 . Dakle, baza u zadanoj matrici je bilo koja matrica oblika . Dakle, baza u zadanoj matrici je bilo koja matrica oblika 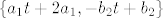 . (Možete uvrstiti i konkretne brojeve za . (Možete uvrstiti i konkretne brojeve za 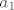 i i 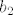 , nije greška.) , nije greška.)
b) Može se riješiti analogno kao i a) zadatak (pa doći u nekakvu kontradikciju, npr. skup polinoma koji ne bi mogao biti baza vektorskog prostora), ali postoji i jedan brži trik: poznato je da su sve matrice istog operatora u bilo kojim bazama slične (odnosno, jedna se može dobiti preko druge množeći je slijeva ili zdesna; konkretno: 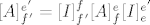 ). Posebno, zadana matrica je slična matrici istog operatora zapisanoj u kanonskom paru baza. ). Posebno, zadana matrica je slična matrici istog operatora zapisanoj u kanonskom paru baza.
E sada, znamo kako djeluje operator. Dakle, izračunamo 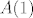 , , 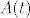 , , 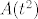 i i 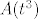 i raspišemo ga preko baze i raspišemo ga preko baze 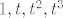 . .
Spominjali smo kako slične matrice imaju neka "zanimljiva, ista svojstva". Primjerice, jednake determinante (što se lako pokaže, a i radilo se na faksu). Sada izračunamo determinante ovih dviju matrica (koje bi trebale biti jednake) i, ako dobijemo da su različite, znamo da zadana matrica nije slična matrici za koju znamo da pripada operatoru - što ujedno znači i da ta matrica nije zapis operatora u nikojem paru baza.
4. Zadatak nije baš šablonski, a ja nemam tekst zadatka, pa ću pokušati iz glave, koliko se sjećam... 
Dakle, recimo da je bio zadan operator 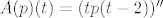 . Operator možemo raspisati tako da napravimo prvu i drugu derivaciju umnoška (i zbroja) polinoma ( . Operator možemo raspisati tako da napravimo prvu i drugu derivaciju umnoška (i zbroja) polinoma (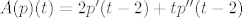 , ako se ne varam). Sada možemo raspisati , ako se ne varam). Sada možemo raspisati 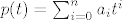 , izračunati , izračunati 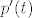 i i 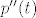 te to uvrstiti u gornju jednakost. te to uvrstiti u gornju jednakost.
Slično kao i na vježbama, kada tražimo jezgru, pretpostavit ćemo da je 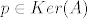 , a za sliku ćemo raspisati , a za sliku ćemo raspisati 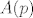 preko nekog sustava izvodnica za preko nekog sustava izvodnica za 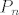 (pa onda, po potrebi, reducirati do baze). (pa onda, po potrebi, reducirati do baze).
E sada, da budem sasvim iskren, malo se žurim, pa ne stignem točno raspisati što se na kraju dobije (  ), ali se nadam da nije problem ako odmah napišem svoj rezultat (ako je, uz to, dobro raspisan; ali ovako otprilike ide): ), ali se nadam da nije problem ako odmah napišem svoj rezultat (ako je, uz to, dobro raspisan; ali ovako otprilike ide):
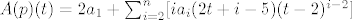 . .
Što sada?
No, uočimo: svaki član sume, kada se raspiše, je polinom 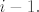 stupnja, odnosno stupnjevi idu od stupnja, odnosno stupnjevi idu od  do do 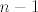 (i vodeći koeficijent je neskrativ). (i vodeći koeficijent je neskrativ). 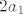 predstavlja slobodni član, stoga je ovo raspis polinoma predstavlja slobodni član, stoga je ovo raspis polinoma 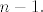 stupnja. stupnja.
Dakle:
1) Ako tražimo jezgru, rješavamo jednadžbu 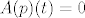 . Ako formiramo skup koji se sastoji od polinoma koji su članovi ove sume (i pridodamo još konstantni polinom), tj. . Ako formiramo skup koji se sastoji od polinoma koji su članovi ove sume (i pridodamo još konstantni polinom), tj. 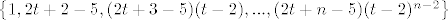 , uočavamo da je to linearno nezavisan skup jer se nijedan element toga skupa ne može prikazati preko svoga prethodnika (svaki član skupa je većeg stupnja od bilo kojeg prethodnog). Stoga su i svi koeficijenti ispred tih elemenata jednaki nuli, tj.: , uočavamo da je to linearno nezavisan skup jer se nijedan element toga skupa ne može prikazati preko svoga prethodnika (svaki član skupa je većeg stupnja od bilo kojeg prethodnog). Stoga su i svi koeficijenti ispred tih elemenata jednaki nuli, tj.: 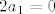 , , 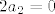 , , 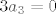 , ..., , ..., 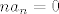 , iz čega proizlazi , iz čega proizlazi 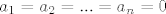 . Dakle, jezgri pripadaju svi polinomi oblika . Dakle, jezgri pripadaju svi polinomi oblika 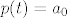 , odnosno konstantni polinomi. , odnosno konstantni polinomi. 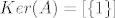 , , 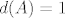 . .
2) Opet, gornji zapis je zapravo raspis po linearno nezavisnom skupu 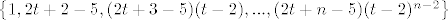 koji je stoga i skup izvodnica za sliku, pa je to baza za koji je stoga i skup izvodnica za sliku, pa je to baza za 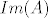 . Elemenata ima . Elemenata ima 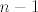 i to su polinomi od i to su polinomi od 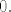 do do 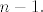 stupnja, dakle stupnja, dakle 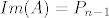 , , 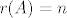 . .
(Uočimo da nam rješenja zadovoljavaju teorem o rangu i defektu.)
Zadnja promjena: Phoenix; 13:17 ned, 12. 6. 2011; ukupno mijenjano 2 put/a.
|





