| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Kika123
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (20:20:11)
Postovi: (C)16
|
|
| [Vrh] |
|
jivek
Forumaš(ica)

Pridružen/a: 30. 10. 2009. (20:22:21)
Postovi: (2)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
Kika123
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (20:20:11)
Postovi: (C)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
ljpalle
Forumaš(ica)

Pridružen/a: 24. 09. 2011. (10:10:43)
Postovi: (22)16
|
 Postano: 19:27 ned, 2. 10. 2011 Naslov: Postano: 19:27 ned, 2. 10. 2011 Naslov: |
    |
|
|
(a) (n povrh k) ... mislim da ne treba objasniti
(b) izaberemo prvo 2k parova i onda neku od dvije osobe iz svakog para, pa je rjesenje 2^(2k) * (n povrh 2k)
(c) suprotno od toga je da se u grupi ne nalazi nijedan par, a to je (b), a ukupan broj grupa je (2n povrh 2k), pa je rjesenje (2n povrh 2k) - 2^(2k) * (n povrh 2k)
(d) prvo biramo ta 2 para na (n povrh 2) nacina, a onda preostaje odabrati ostale ljude tako da ne bude nijedan par, tj. slicno kao u (b), pa je konacno rjesenje (n povrh 2) * 2^(2k - 4) * (n-2 povrh 2k-4)
Ne jamcim tocnost rezultata :P .
(a) (n povrh k) ... mislim da ne treba objasniti
(b) izaberemo prvo 2k parova i onda neku od dvije osobe iz svakog para, pa je rjesenje 2^(2k) * (n povrh 2k)
(c) suprotno od toga je da se u grupi ne nalazi nijedan par, a to je (b), a ukupan broj grupa je (2n povrh 2k), pa je rjesenje (2n povrh 2k) - 2^(2k) * (n povrh 2k)
(d) prvo biramo ta 2 para na (n povrh 2) nacina, a onda preostaje odabrati ostale ljude tako da ne bude nijedan par, tj. slicno kao u (b), pa je konacno rjesenje (n povrh 2) * 2^(2k - 4) * (n-2 povrh 2k-4)
Ne jamcim tocnost rezultata  . .
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 9:20 pon, 3. 10. 2011 Naslov: Postano: 9:20 pon, 3. 10. 2011 Naslov: |
    |
|
|
Ovo pod b) mi nije cisto jasno, ako je moguce malo detaljnije objasnjenje zasto..
Nije mi jasno to sto u zadatku se navodi da odaberemo grupu od 2k LJUDI, sto po mom znaci, k PAROVA,
zasto sad pod b) trazimo 2k parova, i jos povrh svega odabiremo dvije osobe iz svakog para...
Hvala :oops:
Ovo pod b) mi nije cisto jasno, ako je moguce malo detaljnije objasnjenje zasto..
Nije mi jasno to sto u zadatku se navodi da odaberemo grupu od 2k LJUDI, sto po mom znaci, k PAROVA,
zasto sad pod b) trazimo 2k parova, i jos povrh svega odabiremo dvije osobe iz svakog para...
Hvala 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 9:46 pon, 3. 10. 2011 Naslov: Postano: 9:46 pon, 3. 10. 2011 Naslov: |
    |
|
|
To što biraš grupu od [tex]2k[/tex] ljudi ne znači da ćeš odabrati [tex]k[/tex] parova jer možeš odabrati i samo jednu osobu iz nekog od [tex]n[/tex] početnih parova, a možda i nijednu. Recimo, ako je [tex]k=3[/tex] i [tex]n=5[/tex], znači da biraš [tex]6[/tex] ljudi od njih [tex]10[/tex] koji su formirani u [tex]5[/tex] parova, recimo: [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}, a_{9}-a_{10}[/tex]. Možeš izabrati, recimo, [tex]a_{1}, a_{2}, a_{3}, a_{5}, a_{7}, a_{9}[/tex], a, kao što vidiš, samo je jedan par u ovoj grupi, a ne [tex]k=3[/tex]. :)
U b) zadatku moraš odabrati [tex]2k[/tex] ljudi iz [tex]n[/tex] parova tako da nijedna dva nisu u paru. Ovdje odabireš [tex]2k[/tex] parova zato što ćeš onda iz svakog od tog para odabrati točno jednu osobu, a to ti garantira sljedeće:
1) Iz svakog od [tex]2k[/tex] para po jedna osoba - sveukupno smo odabrali [tex]2k[/tex] osoba.
2) Ako je par odabran kao jedan od onih [tex]2k[/tex], uzeli smo samo jednu osobu, dakle taj par neće biti zajedno u traženoj grupi. Ako uopće nije odabran, nitko iz tog para neće biti u traženoj grupi, pa ni onda nemamo zajedničkog para.
Primjer? [tex]k=2[/tex], [tex]n=5[/tex], parovi [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}, a_{9}-a_{10}[/tex].
Izaberimo [tex]2k=4[/tex] para: [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}[/tex]
Iz svakog para po jedna osoba: [tex]a_{1}, a_{4}, a_{6}, a_{7}[/tex]
I tako otprilike vidimo da naš "algoritam" funkcionira. :)
Kolega je već napisao konačno rješenje. :)
To što biraš grupu od [tex]2k[/tex] ljudi ne znači da ćeš odabrati [tex]k[/tex] parova jer možeš odabrati i samo jednu osobu iz nekog od [tex]n[/tex] početnih parova, a možda i nijednu. Recimo, ako je [tex]k=3[/tex] i [tex]n=5[/tex], znači da biraš [tex]6[/tex] ljudi od njih [tex]10[/tex] koji su formirani u [tex]5[/tex] parova, recimo: [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}, a_{9}-a_{10}[/tex]. Možeš izabrati, recimo, [tex]a_{1}, a_{2}, a_{3}, a_{5}, a_{7}, a_{9}[/tex], a, kao što vidiš, samo je jedan par u ovoj grupi, a ne [tex]k=3[/tex]. 
U b) zadatku moraš odabrati [tex]2k[/tex] ljudi iz [tex]n[/tex] parova tako da nijedna dva nisu u paru. Ovdje odabireš [tex]2k[/tex] parova zato što ćeš onda iz svakog od tog para odabrati točno jednu osobu, a to ti garantira sljedeće:
1) Iz svakog od [tex]2k[/tex] para po jedna osoba - sveukupno smo odabrali [tex]2k[/tex] osoba.
2) Ako je par odabran kao jedan od onih [tex]2k[/tex], uzeli smo samo jednu osobu, dakle taj par neće biti zajedno u traženoj grupi. Ako uopće nije odabran, nitko iz tog para neće biti u traženoj grupi, pa ni onda nemamo zajedničkog para.
Primjer? [tex]k=2[/tex], [tex]n=5[/tex], parovi [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}, a_{9}-a_{10}[/tex].
Izaberimo [tex]2k=4[/tex] para: [tex]a_{1}-a_{2}, a_{3}-a_{4}, a_{5}-a_{6}, a_{7}-a_{8}[/tex]
Iz svakog para po jedna osoba: [tex]a_{1}, a_{4}, a_{6}, a_{7}[/tex]
I tako otprilike vidimo da naš "algoritam" funkcionira. 
Kolega je već napisao konačno rješenje. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:37 pon, 3. 10. 2011 Naslov: Postano: 14:37 pon, 3. 10. 2011 Naslov: |
    |
|
|
Hvala!
Moze jos pomoc oko 7.zadatka, ne znam da li razmisljam pravilno, naime:
neka je A=(2,3), segment [B=(4,4), C=(4,5)], D=(7,7)
Prvo: izracunala sam put od (0,0) do A, sto mi iznosi (5 povrh 2),
drugo: izracunala sam put od A do B, sto mi iznosi (3 povrh 2)
trece: put od B do C je 1, :oops: , ako se ne varam, da li ti mozemo jednosavno iz slike zakljuciti?
S tom jedinicom iz treceg koraka, ZNACI SVA 3 KORAKA SAD MNOZIMO: (5 povrh 2) * ( 3 povrh 2) * 1 = 30
cetvrto: hmm, sad tu stekam... po primjeru iz skripte, da li bi trebalo od ukupnog br.puteva ( m+n povrh m) oduzeti 14 i jos put od C do D, i od D do (m,n) ?
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
Za 6. zadatak ne znam kako iskoristiti uvjete za x-eve. :S
Hvala!
Moze jos pomoc oko 7.zadatka, ne znam da li razmisljam pravilno, naime:
neka je A=(2,3), segment [B=(4,4), C=(4,5)], D=(7,7)
Prvo: izracunala sam put od (0,0) do A, sto mi iznosi (5 povrh 2),
drugo: izracunala sam put od A do B, sto mi iznosi (3 povrh 2)
trece: put od B do C je 1,  , ako se ne varam, da li ti mozemo jednosavno iz slike zakljuciti? , ako se ne varam, da li ti mozemo jednosavno iz slike zakljuciti?
S tom jedinicom iz treceg koraka, ZNACI SVA 3 KORAKA SAD MNOZIMO: (5 povrh 2) * ( 3 povrh 2) * 1 = 30
cetvrto: hmm, sad tu stekam... po primjeru iz skripte, da li bi trebalo od ukupnog br.puteva ( m+n povrh m) oduzeti 14 i jos put od C do D, i od D do (m,n) ?
Added after 16 minutes:
Za 6. zadatak ne znam kako iskoristiti uvjete za x-eve. :S
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 14:53 pon, 3. 10. 2011 Naslov: Postano: 14:53 pon, 3. 10. 2011 Naslov: |
    |
|
|
Prva tri si skroz dobro napravila :)
sad trebas doci od (4,5) do (m,n) bez (7.7)
to racunamo tako da prebrojimo ukupan broj mogucih puteva od (4,5) do (m,n) i oduzmemo one koji nam ne pasu, to jest one koji sadrze (7,7):
4) Ukupan broj puteva od (4,5) do (m,n) je [latex]{m-4+n-5 \choose m-4}={m+n-9 \choose m-4}[/latex]
5) Broj puteva koji nam ne pasu je
(od (4,5) do (7,7)) - isto kao pocetni korak, dobije se [latex]{5 \choose 2}[/latex]
(od (7,7) do (m,n)) slicno, rezultat: [latex]{m+n-14 \choose m-7}[/latex]
dakle ukupno [latex]{m+n-14 \choose m-7}{5 \choose 2}[/latex]
Sad od koraka 4 oduzmemo korak broj 5 i sve pomnozimo s onim dobivenim u prva 3, i to je to.
6. zadatak:
ako ti je zadan uvjet [latex]x_i \geq a_i[/latex], to sredis supstitucijom [latex]y_i=x_i-a_i[/latex]. Sad ti se pocetna jednadzba samo malo promijenila, a uvjet je bolji: [latex]y_i\geq 0[/latex]
Prva tri si skroz dobro napravila 
sad trebas doci od (4,5) do (m,n) bez (7.7)
to racunamo tako da prebrojimo ukupan broj mogucih puteva od (4,5) do (m,n) i oduzmemo one koji nam ne pasu, to jest one koji sadrze (7,7):
4) Ukupan broj puteva od (4,5) do (m,n) je 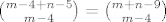
5) Broj puteva koji nam ne pasu je
(od (4,5) do (7,7)) - isto kao pocetni korak, dobije se 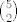
(od (7,7) do (m,n)) slicno, rezultat: 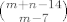
dakle ukupno 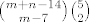
Sad od koraka 4 oduzmemo korak broj 5 i sve pomnozimo s onim dobivenim u prva 3, i to je to.
6. zadatak:
ako ti je zadan uvjet 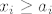 , to sredis supstitucijom , to sredis supstitucijom 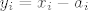 . Sad ti se pocetna jednadzba samo malo promijenila, a uvjet je bolji: . Sad ti se pocetna jednadzba samo malo promijenila, a uvjet je bolji: 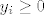
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 15:22 pon, 3. 10. 2011 Naslov: Postano: 15:22 pon, 3. 10. 2011 Naslov: |
    |
|
|
Na primjeru ce bit jasnije valjda:
imamo [latex]x_1+\dots+x_6=66[/latex]
uvjeti su [latex]x_1\geq 3[/latex], ...
sad, ako stavimo [latex]y_1=x_1-3[/latex], pocetna jednadzba se mijenja u [latex]y_1+x_2+\dots+x_6=63[/latex].
Sad tako napravis zamjenu na svima, dobijes onakvu jednadzbu kakvima ste brojali rjesenja na vjezbama/predavanjima - jedini uvjet na sumande je da su svi nenegativni.
Zapravo, [latex]x_3[/latex] je ogranicen i odozgo, al to se rijesi tako da prebrojis sva rjesenja jednadzbe, pa onda oduzmes ona u kojima je [latex]x_3[/latex] veci od 8 (javi ako treba to raspisati)
Na primjeru ce bit jasnije valjda:
imamo 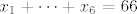
uvjeti su  , ... , ...
sad, ako stavimo 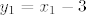 , pocetna jednadzba se mijenja u , pocetna jednadzba se mijenja u  . .
Sad tako napravis zamjenu na svima, dobijes onakvu jednadzbu kakvima ste brojali rjesenja na vjezbama/predavanjima - jedini uvjet na sumande je da su svi nenegativni.
Zapravo, 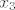 je ogranicen i odozgo, al to se rijesi tako da prebrojis sva rjesenja jednadzbe, pa onda oduzmes ona u kojima je je ogranicen i odozgo, al to se rijesi tako da prebrojis sva rjesenja jednadzbe, pa onda oduzmes ona u kojima je 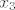 veci od 8 (javi ako treba to raspisati) veci od 8 (javi ako treba to raspisati)
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 21:32 pon, 3. 10. 2011 Naslov: Postano: 21:32 pon, 3. 10. 2011 Naslov: |
    |
|
|
Ovako, uzela sam y3= x3 - 3 , i ostale y sam uvrstila u jednazbu i izjednacila s 45, broj rjesenja mi je ispalo (50 povrh 5), jos treba oduzeti ono sto je vece od 8, molila bih to da jos malo raspises.
2. pitanje: 4.zad - c) 11*6!*7!
d) 2 * 8! ?
3.zad - a) 4*10*10*10
b) 5*10*10*10
c) 4*10*10*4
d) 8*7*6*5
e) 9*8*7*2
f) 7*8*8*5
2.zad - hmm, 24 djelitelja od 630 (od toga 5 djeljivo s 3), a 360 od
151200 (od toga 11 djeljivo s 3), jel to dobro?
Ovako, uzela sam y3= x3 - 3 , i ostale y sam uvrstila u jednazbu i izjednacila s 45, broj rjesenja mi je ispalo (50 povrh 5), jos treba oduzeti ono sto je vece od 8, molila bih to da jos malo raspises.
2. pitanje: 4.zad - c) 11*6!*7!
d) 2 * 8! ?
3.zad - a) 4*10*10*10
b) 5*10*10*10
c) 4*10*10*4
d) 8*7*6*5
e) 9*8*7*2
f) 7*8*8*5
2.zad - hmm, 24 djelitelja od 630 (od toga 5 djeljivo s 3), a 360 od
151200 (od toga 11 djeljivo s 3), jel to dobro?
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
akolak
Forumaš(ica)

Pridružen/a: 27. 12. 2010. (16:52:59)
Postovi: (1D)16
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
|
| [Vrh] |
|
|








