| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:57 uto, 11. 10. 2011 Naslov: Postano: 20:57 uto, 11. 10. 2011 Naslov: |
    |
|
|
Evo ti par hintova. :)
(a) Vrijedi [tex]\mathbb{P}(\{\text{iz A se može doći u C cestom}\}) = \mathbb{P}(\{\text{iz A se može doći u B cestom} \textbf{ i } \text{iz B se može doći u C cestom}\}) = \mathbb{P}(\{\text{iz A se cestom može doći u B}) \cdot \mathbb{P}(\text{iz B se cestom može doći u C}\})[/tex]. Prva jednakost vrijedi jer se cestom ne može direktno doći iz A u C, a druga zbog nezavisnosti. Svaku od vjerojatnosti u produktu je možda lakše izračunati preko suprotnog događaja.
Rješenje je [spoiler][tex](1 - p^2)^2[/tex][/spoiler]
(b) Uočimo da iz A u C možemo doći ili cestom ili željeznicom (nema potrebe za kombiniranjem dvaju načina prijevoza). Označimo [tex]X := \{\text{može se doći u C}\}[/tex], [tex]Y := \{\text{može se doći u C cestom}\}[/tex] i [tex]Z := \{\text{može se doći u C željeznicom}\}[/tex]. Po početnoj napomeni slijedi [tex]X = Y \cup Z[/tex]. Probaj [tex]\mathbb{P}(x)[/tex] izračunati sa [tex]\mathbb{P}(Y) + \mathbb{P}(Z) - \mathbb{P}(Y)\mathbb{P}(Z)[/tex], [tex]1 - \mathbb{P}(Y^C) \mathbb{P}(Z^C)[/tex] i [tex]\mathbb{P}(X \mid Z) \mathbb{P}(Z) + \mathbb{P}(X \mid Z^C) \mathbb{P}(Z^C)[/tex].
Konačno rješenje: [spoiler][tex]1 - 2 p^3 + p^5[/tex][/spoiler]
(c) Koristeći gornje oznake, traži se [tex]\mathbb{P}(Z^C \mid X)[/tex]. Rješenje se dobi koristeći definiciju uvjetne vjerojatnosti: [spoiler][tex]\displaystyle \frac{p (1 - p^2)^2}{1 - 2 p^3 + p^5}[/tex][/spoiler]
Evo ti par hintova. 
(a) Vrijedi [tex]\mathbb{P}(\{\text{iz A se može doći u C cestom}\}) = \mathbb{P}(\{\text{iz A se može doći u B cestom} \textbf{ i } \text{iz B se može doći u C cestom}\}) = \mathbb{P}(\{\text{iz A se cestom može doći u B}) \cdot \mathbb{P}(\text{iz B se cestom može doći u C}\})[/tex]. Prva jednakost vrijedi jer se cestom ne može direktno doći iz A u C, a druga zbog nezavisnosti. Svaku od vjerojatnosti u produktu je možda lakše izračunati preko suprotnog događaja.
Rješenje je | Spoiler [hidden; click to show]: | [tex](1 - p^2)^2[/tex] |
(b) Uočimo da iz A u C možemo doći ili cestom ili željeznicom (nema potrebe za kombiniranjem dvaju načina prijevoza). Označimo [tex]X := \{\text{može se doći u C}\}[/tex], [tex]Y := \{\text{može se doći u C cestom}\}[/tex] i [tex]Z := \{\text{može se doći u C željeznicom}\}[/tex]. Po početnoj napomeni slijedi [tex]X = Y \cup Z[/tex]. Probaj [tex]\mathbb{P}(x)[/tex] izračunati sa [tex]\mathbb{P}(Y) + \mathbb{P}(Z) - \mathbb{P}(Y)\mathbb{P}(Z)[/tex], [tex]1 - \mathbb{P}(Y^C) \mathbb{P}(Z^C)[/tex] i [tex]\mathbb{P}(X \mid Z) \mathbb{P}(Z) + \mathbb{P}(X \mid Z^C) \mathbb{P}(Z^C)[/tex].
Konačno rješenje: | Spoiler [hidden; click to show]: | [tex]1 - 2 p^3 + p^5[/tex] |
(c) Koristeći gornje oznake, traži se [tex]\mathbb{P}(Z^C \mid X)[/tex]. Rješenje se dobi koristeći definiciju uvjetne vjerojatnosti: | Spoiler [hidden; click to show]: | [tex]\displaystyle \frac{p (1 - p^2)^2}{1 - 2 p^3 + p^5}[/tex] |
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 18:50 čet, 13. 10. 2011 Naslov: Postano: 18:50 čet, 13. 10. 2011 Naslov: |
    |
|
|
bi li neko mogao objasniti kako intuitivno shvaca nezavisnost dogadaja?
Evo konkretno primjer sto me muci... Biramo nasumicno broj iz skupa {1,2,...,9} tako da je svaki ishod jednako vjerojatan. Sad promatramo dva dogadaja:
A={izabrali smo 1,2 ili 3}
B={izabrali smo 3,4 ili 5}
Sad imamo P(A)=3/9=P(B), P(A&B)=1/9
pa je P(A&B)=P(A)*P(B)=1/9, dakle A i B su "nezavisni"
Ali...ako isto tako nasumicno biramo broj,ali iz skupa (1,2,...,10}
onda je P(A)=3/10=P(B), P(A&B)=1/10
pa je P(A&B) =/= P(A)*P(B),dakle u ovom slucaju A i B nisu nezavisni
Nije mi jasno kako dodatak ovog jednog elementa u skup mijenja jesu li A i B nezavisni. Jel ima neka greska u razmisljanja ili sta :shock:
bi li neko mogao objasniti kako intuitivno shvaca nezavisnost dogadaja?
Evo konkretno primjer sto me muci... Biramo nasumicno broj iz skupa {1,2,...,9} tako da je svaki ishod jednako vjerojatan. Sad promatramo dva dogadaja:
A={izabrali smo 1,2 ili 3}
B={izabrali smo 3,4 ili 5}
Sad imamo P(A)=3/9=P(B), P(A&B)=1/9
pa je P(A&B)=P(A)*P(B)=1/9, dakle A i B su "nezavisni"
Ali...ako isto tako nasumicno biramo broj,ali iz skupa (1,2,...,10}
onda je P(A)=3/10=P(B), P(A&B)=1/10
pa je P(A&B) =/= P(A)*P(B),dakle u ovom slucaju A i B nisu nezavisni
Nije mi jasno kako dodatak ovog jednog elementa u skup mijenja jesu li A i B nezavisni. Jel ima neka greska u razmisljanja ili sta 
|
|
| [Vrh] |
|
akolak
Forumaš(ica)

Pridružen/a: 27. 12. 2010. (16:52:59)
Postovi: (1D)16
|
 Postano: 1:16 pet, 14. 10. 2011 Naslov: Postano: 1:16 pet, 14. 10. 2011 Naslov: |
    |
|
|
[quote="kikzmyster"]bi li neko mogao objasniti kako intuitivno shvaca nezavisnost dogadaja?
Evo konkretno primjer sto me muci... Biramo nasumicno broj iz skupa {1,2,...,9} tako da je svaki ishod jednako vjerojatan. Sad promatramo dva dogadaja:
A={izabrali smo 1,2 ili 3}
B={izabrali smo 3,4 ili 5}
Sad imamo P(A)=3/9=P(B), P(A&B)=1/9
pa je P(A&B)=P(A)*P(B)=1/9, dakle A i B su "nezavisni"
Ali...ako isto tako nasumicno biramo broj,ali iz skupa (1,2,...,10}
onda je P(A)=3/10=P(B), P(A&B)=1/10
pa je P(A&B) =/= P(A)*P(B),dakle u ovom slucaju A i B nisu nezavisni
Nije mi jasno kako dodatak ovog jednog elementa u skup mijenja jesu li A i B nezavisni. Jel ima neka greska u razmisljanja ili sta :shock:[/quote]
Po mojoj slobodnoj intuiciji (kasno navečer) nezavisni skupovi su oni kod kojih vjerojatnost da se dogodi jedan ne ovisi o tome da li se dogodio drugi. (Odnosno da je uvijek jednaka)
Dakle bacim prvu kocku i dobijem neki broj. Taj broj mi nikako neće utjecat na vjerojatnost da u drugom bacanju dobijem recimo 6.
Uzmimo tvoj prvi slučaj. Šansa da se dogodi B ako znamo da se A nije dogodio je 1/3. Šansa da se dogodi B ako znamo da se A dogodio je opet 1/3. Dakle svejedno nam je jel se dogodio ili nije.
Uzmimo tvoj drugi slučaj. Ako se A nije dogodio, šansa da se dogodi B je 2/7. Ako se dogodio A, onda je šansa 1/3. Tu nam je dakle važno jel se A dogodio ili nije.
| kikzmyster (napisa): | bi li neko mogao objasniti kako intuitivno shvaca nezavisnost dogadaja?
Evo konkretno primjer sto me muci... Biramo nasumicno broj iz skupa {1,2,...,9} tako da je svaki ishod jednako vjerojatan. Sad promatramo dva dogadaja:
A={izabrali smo 1,2 ili 3}
B={izabrali smo 3,4 ili 5}
Sad imamo P(A)=3/9=P(B), P(A&B)=1/9
pa je P(A&B)=P(A)*P(B)=1/9, dakle A i B su "nezavisni"
Ali...ako isto tako nasumicno biramo broj,ali iz skupa (1,2,...,10}
onda je P(A)=3/10=P(B), P(A&B)=1/10
pa je P(A&B) =/= P(A)*P(B),dakle u ovom slucaju A i B nisu nezavisni
Nije mi jasno kako dodatak ovog jednog elementa u skup mijenja jesu li A i B nezavisni. Jel ima neka greska u razmisljanja ili sta  |
Po mojoj slobodnoj intuiciji (kasno navečer) nezavisni skupovi su oni kod kojih vjerojatnost da se dogodi jedan ne ovisi o tome da li se dogodio drugi. (Odnosno da je uvijek jednaka)
Dakle bacim prvu kocku i dobijem neki broj. Taj broj mi nikako neće utjecat na vjerojatnost da u drugom bacanju dobijem recimo 6.
Uzmimo tvoj prvi slučaj. Šansa da se dogodi B ako znamo da se A nije dogodio je 1/3. Šansa da se dogodi B ako znamo da se A dogodio je opet 1/3. Dakle svejedno nam je jel se dogodio ili nije.
Uzmimo tvoj drugi slučaj. Ako se A nije dogodio, šansa da se dogodi B je 2/7. Ako se dogodio A, onda je šansa 1/3. Tu nam je dakle važno jel se A dogodio ili nije.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:27 ned, 16. 10. 2011 Naslov: Postano: 12:27 ned, 16. 10. 2011 Naslov: |
    |
|
|
Možemo nabrojati sve moguće elementarne događaje (uređeni par starijeg i mlađeg djeteta), pa odrediti vjerojatnost svakog.
[dtex]\begin{array}{c|c}
\text{el. događaj} & \text{vjerojatnost} \\
\hline
(\text{Ivan, sin}) & \frac{1}{2} \cdot p_1 \cdot \frac{1}{2} \\
(\text{Ivan, kći}) & \frac{1}{2} \cdot p_1 \cdot \frac{1}{2} \\
(\text{sin ne Ivan, Ivan}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \cdot p_2 \\
(\text{sin ne Ivan, sin ne Ivan}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \cdot (1 - p_2) \\
(\text{sin ne Ivan, kći}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \\
(\text{kći, Ivan}) & \frac{1}{2} \cdot \frac{1}{2} \cdot p_1 \\
(\text{kći, sin ne Ivan}) & \frac{1}{2} \cdot \frac{1}{2} \cdot (1 - p_1) \\
(\text{kći, kći}) & \frac{1}{2} \cdot \frac{1}{2}
\end{array}[/dtex]
Od nas se traži [tex]\mathbb{P}(\{\text{jedno djete je kći}\} \mid \{\text{jedan sin se zove Ivan}\})[/tex]. Nakon što se to raspiše po definiciji, trebalo bi ispasti da je rješenje [tex]\displaystyle \frac{2 p_1}{3 p_1 + p_2 - p_1 p_2}[/tex].
Eto, nadam se da je sve dobro. :)
EDIT: Čini se da nije sve dobro. :D Zahvala akolak-u. ;)
Možemo nabrojati sve moguće elementarne događaje (uređeni par starijeg i mlađeg djeteta), pa odrediti vjerojatnost svakog.
[dtex]\begin{array}{c|c}
\text{el. događaj} & \text{vjerojatnost} \\
\hline
(\text{Ivan, sin}) & \frac{1}{2} \cdot p_1 \cdot \frac{1}{2} \\
(\text{Ivan, kći}) & \frac{1}{2} \cdot p_1 \cdot \frac{1}{2} \\
(\text{sin ne Ivan, Ivan}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \cdot p_2 \\
(\text{sin ne Ivan, sin ne Ivan}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \cdot (1 - p_2) \\
(\text{sin ne Ivan, kći}) & \frac{1}{2} \cdot (1 - p_1) \cdot \frac{1}{2} \\
(\text{kći, Ivan}) & \frac{1}{2} \cdot \frac{1}{2} \cdot p_1 \\
(\text{kći, sin ne Ivan}) & \frac{1}{2} \cdot \frac{1}{2} \cdot (1 - p_1) \\
(\text{kći, kći}) & \frac{1}{2} \cdot \frac{1}{2}
\end{array}[/dtex]
Od nas se traži [tex]\mathbb{P}(\{\text{jedno djete je kći}\} \mid \{\text{jedan sin se zove Ivan}\})[/tex]. Nakon što se to raspiše po definiciji, trebalo bi ispasti da je rješenje [tex]\displaystyle \frac{2 p_1}{3 p_1 + p_2 - p_1 p_2}[/tex].
Eto, nadam se da je sve dobro. 
EDIT: Čini se da nije sve dobro.  Zahvala akolak-u. Zahvala akolak-u. 
Zadnja promjena: pmli; 12:22 uto, 18. 10. 2011; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
akolak
Forumaš(ica)

Pridružen/a: 27. 12. 2010. (16:52:59)
Postovi: (1D)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:15 pon, 17. 10. 2011 Naslov: Postano: 18:15 pon, 17. 10. 2011 Naslov: |
    |
|
|
Nije problem. :)
[dtex]\mathbb{P}(\{\text{jedno djete je kći}\} \mid \{\text{jedan sin se zove Ivan}\}) = \frac{\mathbb{P}(\{\text{jedno djete je kći i jedan sin se zove Ivan}\})}{\mathbb{P}(\{\text{jedan sin se zove Ivan}\})} = \frac{\mathbb{P}((\text{Ivan, kći})) + \mathbb{P}((\text{kći, Ivan}))}{\mathbb{P}((\text{Ivan, sin})) + \mathbb{P}((\text{Ivan, kći})) + \mathbb{P}((\text{sin ne Ivan, Ivan})) + \mathbb{P}((\text{kći, Ivan}))}[/dtex]
Nije problem. 
[dtex]\mathbb{P}(\{\text{jedno djete je kći}\} \mid \{\text{jedan sin se zove Ivan}\}) = \frac{\mathbb{P}(\{\text{jedno djete je kći i jedan sin se zove Ivan}\})}{\mathbb{P}(\{\text{jedan sin se zove Ivan}\})} = \frac{\mathbb{P}((\text{Ivan, kći})) + \mathbb{P}((\text{kći, Ivan}))}{\mathbb{P}((\text{Ivan, sin})) + \mathbb{P}((\text{Ivan, kći})) + \mathbb{P}((\text{sin ne Ivan, Ivan})) + \mathbb{P}((\text{kći, Ivan}))}[/dtex]
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 10:49 ned, 6. 11. 2011 Naslov: Postano: 10:49 ned, 6. 11. 2011 Naslov: |
    |
|
|
1.42.
Pa ovaj niz ide [latex]\frac{1}{3}, \frac{1}{5}, \frac{1}{7} ...[/latex] pa ako uzmem neki događaj A takav da je [latex]P(A) = \frac{1}{2} [/latex] i od njega ''napravim'' konstantan niz A, A, A, A... vrijedit će ovo svojstvo.
(Jer je [latex]\frac{1}{2} \geq \frac{1}{2n+1}, \forall n \in \mathbb{N}[/latex])
Da, postoji! :)
1.43
Ajmo malo raspisat ove trokutiće prvo:
[latex]P(A \bigtriangleup B) = P( (A \cup B) \backslash (A \cap B) ) = P(A \cup B) - P(A \cap B) [/latex] (odakle sam ''izvukao'' ovaj minus?)
Sad ovu drugu nejednakost možemo pisati ovako:
[latex]P((A \cup B)) - P(A \cap B) + P(B \cup C) - P(B \cap C) < \frac{2}{3} [/latex]
što opet možemo malo urediti na:
[latex]P(A) + 2P(B) + P(C) < \frac{2}{3} + 2P(B \cap C) + 2P(A \cap B) [/latex]
E sad ja kažem da to ne može vrijediti zbog one prve nejednakosti. Razmisli malo! :)
Nisam jako zao, pa ako ti ne bude jasno, napisat ću ja sve.
Hint: koristi da je vjerojatnost bilo čega veća ili jednaka nuli.
1.42.
Pa ovaj niz ide 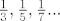 pa ako uzmem neki događaj A takav da je pa ako uzmem neki događaj A takav da je 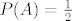 i od njega ''napravim'' konstantan niz A, A, A, A... vrijedit će ovo svojstvo. i od njega ''napravim'' konstantan niz A, A, A, A... vrijedit će ovo svojstvo.
(Jer je 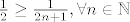 ) )
Da, postoji! 
1.43
Ajmo malo raspisat ove trokutiće prvo:
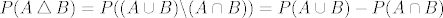 (odakle sam ''izvukao'' ovaj minus?) (odakle sam ''izvukao'' ovaj minus?)
Sad ovu drugu nejednakost možemo pisati ovako:
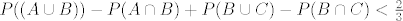
što opet možemo malo urediti na:
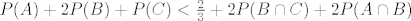
E sad ja kažem da to ne može vrijediti zbog one prve nejednakosti. Razmisli malo! 
Nisam jako zao, pa ako ti ne bude jasno, napisat ću ja sve.
Hint: koristi da je vjerojatnost bilo čega veća ili jednaka nuli.
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 10:02 pon, 7. 11. 2011 Naslov: Postano: 10:02 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote="888"]:D e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B 8) )
PS:jel može još malo pomoći oko 2.14: kolika je vjerojatnost da će u n bacanja simetrične kockice pasti neparan broj sestica?[/quote]
Šestica pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da šestica padne točno [tex]k[/tex] puta iznosi [tex]{n \choose k}(1/6)^k(5/6)^{n-k}[/tex]. Zašto? Biramo u kojih [tex]k[/tex] bacanja će pasti šestica, to je [tex]{n\choose k}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^k[/tex] (vjerojatnost da u tih [tex]k[/tex] bacanja padne šestica) puta [tex](5/6)^{n-k}[/tex] (vjerojatnost da u preostalih [tex]n-k[/tex] bacanja ne padne šestica).
Znači rješenje je [latex]\displaystyle\sum_{\substack{
1\le k\le n \\
k \mathrm{ neparan}
}}{n \choose k}(1/6)^k(5/6)^{n-k} = \displaystyle\sum_{\substack{
1\le k\le n \\
k \mathrm{ neparan}
}}{n \choose k}\frac{5^{n-k}}{6^n}[/latex]
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
[quote="meda"]trenutacno sam poprilicno zatupljena pa ako bi neko napisao zasto je u 4.a) odgovor 1/3 bila bih zahvalna
http://web.math.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf[/quote]
[tex]P(prvi | ne.treci) = P(prvi | treci^c) = \mathrm{ po. formuli .za. uvjetnu .vjerojatnost } = \displaystyle\frac{P(prvi \cap treci^c)}{P(treci^c)} = \frac{P(\{1,3\} \cap \{2,3,5\})}{P(\{2,3,5\})} = \frac{P(\{3\})}{P(\{2\})+P(\{3\})+P(\{5\})} = \frac{2/9}{6/9} = \frac 1 3[/tex]
| 888 (napisa): |  e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B  ) )
PS:jel može još malo pomoći oko 2.14: kolika je vjerojatnost da će u n bacanja simetrične kockice pasti neparan broj sestica? |
Šestica pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da šestica padne točno [tex]k[/tex] puta iznosi [tex]{n \choose k}(1/6)^k(5/6)^{n-k}[/tex]. Zašto? Biramo u kojih [tex]k[/tex] bacanja će pasti šestica, to je [tex]{n\choose k}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^k[/tex] (vjerojatnost da u tih [tex]k[/tex] bacanja padne šestica) puta [tex](5/6)^{n-k}[/tex] (vjerojatnost da u preostalih [tex]n-k[/tex] bacanja ne padne šestica).
Znači rješenje je 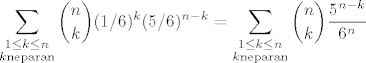
Added after 12 minutes:
[tex]P(prvi | ne.treci) = P(prvi | treci^c) = \mathrm{ po. formuli .za. uvjetnu .vjerojatnost } = \displaystyle\frac{P(prvi \cap treci^c)}{P(treci^c)} = \frac{P(\{1,3\} \cap \{2,3,5\})}{P(\{2,3,5\})} = \frac{P(\{3\})}{P(\{2\})+P(\{3\})+P(\{5\})} = \frac{2/9}{6/9} = \frac 1 3[/tex]
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 10:52 pon, 7. 11. 2011 Naslov: Postano: 10:52 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote="satja"][quote="888"]:D e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B 8) )
PS:jel može još malo pomoći oko 2.14: kolika je vjerojatnost da će u n bacanja simetrične kockice pasti neparan broj sestica?[/quote]
Šestica pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da šestica padne točno [tex]k[/tex] puta iznosi [tex]{n \choose k}(1/6)^k(5/6)^{n-k}[/tex]. Zašto? Biramo u kojih [tex]k[/tex] bacanja će pasti šestica, to je [tex]{n\choose k}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^k[/tex] (vjerojatnost da u tih [tex]k[/tex] bacanja padne šestica) puta [tex](5/6)^{n-k}[/tex] (vjerojatnost da u preostalih [tex]n-k[/tex] bacanja ne padne šestica).
Znači rješenje je [latex]\displaystyle\sum_{\substack{
1\le k\le n \\
k \mathrm{ neparan}
}}{n \choose k}(1/6)^k(5/6)^{n-k} = \displaystyle\sum_{\substack{
1\le k\le n \\
k \mathrm{ neparan}
}}{n \choose k}\frac{5^{n-k}}{6^n}[/latex][/quote]
Taj se zadatak može riješiti "egzaktno" (možda i ovim načinom, ne znam). Nama su prošle godine (barem u mojoj grupi) pokazali kako to riješiti rekurzijama. Ako još niste radili rekurzije na diskretnoj, onda nema smisla da ovo objašnjavam, ali ok. :)
Označimo s [latex]p_n[/latex] traženu vjerojatnost. Sad nas zanima je li u prvom bacanju pala ili nije pala šestica, i kako o tome ovisi [latex]p_n[/latex]. Po formuli potpune vjerojatnosti slijedi [latex]\displaystyle p_n = \frac{5}{6} p_{n - 1} + \frac{1}{6} (1 - p_{n - 1})[/latex], tj. ako u prvom bacanju ne padne šestica, u preostalih [latex]n - 1[/latex] ih mora pasti neparan broj, a obratno ako je šestica pala u prvom bacanju. Uz početni uvjet [latex]\displaystyle p_1 = \frac{1}{6}[/latex] dobivamo rekurziju koju možemo riješiti.
| satja (napisa): | | 888 (napisa): |  e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B e super, skužila.. hvalaaaa (minus si izvukao jer je A presjek B podskup od A U B  ) )
PS:jel može još malo pomoći oko 2.14: kolika je vjerojatnost da će u n bacanja simetrične kockice pasti neparan broj sestica? |
Šestica pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da šestica padne točno [tex]k[/tex] puta iznosi [tex]{n \choose k}(1/6)^k(5/6)^{n-k}[/tex]. Zašto? Biramo u kojih [tex]k[/tex] bacanja će pasti šestica, to je [tex]{n\choose k}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^k[/tex] (vjerojatnost da u tih [tex]k[/tex] bacanja padne šestica) puta [tex](5/6)^{n-k}[/tex] (vjerojatnost da u preostalih [tex]n-k[/tex] bacanja ne padne šestica).
Znači rješenje je 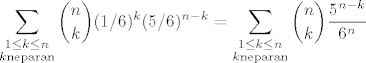 |
Taj se zadatak može riješiti "egzaktno" (možda i ovim načinom, ne znam). Nama su prošle godine (barem u mojoj grupi) pokazali kako to riješiti rekurzijama. Ako još niste radili rekurzije na diskretnoj, onda nema smisla da ovo objašnjavam, ali ok. 
Označimo s 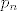 traženu vjerojatnost. Sad nas zanima je li u prvom bacanju pala ili nije pala šestica, i kako o tome ovisi traženu vjerojatnost. Sad nas zanima je li u prvom bacanju pala ili nije pala šestica, i kako o tome ovisi 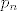 . Po formuli potpune vjerojatnosti slijedi . Po formuli potpune vjerojatnosti slijedi 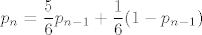 , tj. ako u prvom bacanju ne padne šestica, u preostalih , tj. ako u prvom bacanju ne padne šestica, u preostalih 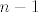 ih mora pasti neparan broj, a obratno ako je šestica pala u prvom bacanju. Uz početni uvjet ih mora pasti neparan broj, a obratno ako je šestica pala u prvom bacanju. Uz početni uvjet 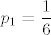 dobivamo rekurziju koju možemo riješiti. dobivamo rekurziju koju možemo riješiti.
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 15:25 pon, 7. 11. 2011 Naslov: Postano: 15:25 pon, 7. 11. 2011 Naslov: |
    |
|
|
Koji te dio točno muči?
Imaš tri događaja
A = {zbroj brojeva na kockama je 25}
B = {bar jednom padne 5}
C = {produkt dobivenih brojeva je djeljiv sa 10}
Trebaš izračunati P(A U B U C), tako da će ti trebati i vjerojatnosti događaja A presjek B, A presjek C, B presjek C i A presjek B presjek C...
Vidiš da tu ima dosta računanja, pa mi se ne da sad sve baš pisati... xD
Da prebrojiš na koliko se načina može dogoditi A staviš:
[latex]x_1 + x_2 + x_3 + x_4 + x_5 = 25, 1 \leq x_i \leq 6, i = 1, ..., 6[/latex]
što bi ti trebalo biti poznato sa diskretne.
B si vjerojatno već vidjela.
C - produkt brojeva će biti djeljiv sa 10 ako se pojave bar jedna dvojka i bar jedna petica
Na kojem si dijelu od ovih točno zapela?
Koji te dio točno muči?
Imaš tri događaja
A = {zbroj brojeva na kockama je 25}
B = {bar jednom padne 5}
C = {produkt dobivenih brojeva je djeljiv sa 10}
Trebaš izračunati P(A U B U C), tako da će ti trebati i vjerojatnosti događaja A presjek B, A presjek C, B presjek C i A presjek B presjek C...
Vidiš da tu ima dosta računanja, pa mi se ne da sad sve baš pisati... xD
Da prebrojiš na koliko se načina može dogoditi A staviš:
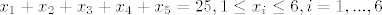
što bi ti trebalo biti poznato sa diskretne.
B si vjerojatno već vidjela.
C - produkt brojeva će biti djeljiv sa 10 ako se pojave bar jedna dvojka i bar jedna petica
Na kojem si dijelu od ovih točno zapela?
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
|














