| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
grubby
Forumaš(ica)
Pridružen/a: 06. 10. 2010. (15:37:04)
Postovi: (9)16
|
 Postano: 23:39 pon, 31. 10. 2011 Naslov: Postano: 23:39 pon, 31. 10. 2011 Naslov: |
    |
|
|
Što se dokazivanja zatvorenosti tiče,definiramo f-je:
a) [latex]f(x,y,z,w)=xw-yz[/latex]
b) [latex]g(x,y,z,w)=||(x,y)||_1+||(z,w)||_\infty[/latex]
Te funkcije su neprekidne zbog toga što je produkt neprekidnih f-ja neprekidan,sve norme neprekidne,njihova suma je neprekidna,itd,itd..
Vidimo da je:
[latex]a) K=f^{-1}(\{0\})[/latex]
[latex]b) L=g^{-1}([0,1])[/latex]
i primjenom TM 1.9. http://web.math.hr/nastava/difraf/dif/vjezbe4.pdf slijedi da su K i L zatvoreni skupovi..
Što se dokazivanja zatvorenosti tiče,definiramo f-je:
a) 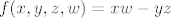
b) 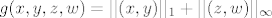
Te funkcije su neprekidne zbog toga što je produkt neprekidnih f-ja neprekidan,sve norme neprekidne,njihova suma je neprekidna,itd,itd..
Vidimo da je:
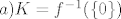
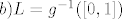
i primjenom TM 1.9. http://web.math.hr/nastava/difraf/dif/vjezbe4.pdf slijedi da su K i L zatvoreni skupovi..
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
blala
Gost
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 19:58 uto, 1. 11. 2011 Naslov: Postano: 19:58 uto, 1. 11. 2011 Naslov: |
    |
|
|
2007.
1. b) Neka je [latex](x_0, y_0, z_0)[/latex] točka u cilindru. Onda je [latex]x_0^2 + y_0^2 < 1[/latex].
[latex]r := 1 - \sqrt{x_0^2+y_0^2} > 0[/latex]. Onda je za [latex](x, y, z) \in K((x_0, y_0, z_0), r)[/latex]
[latex]\sqrt{x^2 + y^2} = d((x, y), (0, 0)) [/latex]
[latex] \leq d((x, y), (x_0, y_0)) + d((x_0, y_0), (0, 0)) [/latex]
[latex] \leq d((x, y, z), (x_0, y_0, z_0)) + d((x_0, y_0), (0, 0))[/latex]
[latex] < 1 - \sqrt{x_0^2+y_0^2} + \sqrt{x_0^2 + y_0^2} [/latex]
[latex]= 1[/latex]
pa je [latex](x, y, z)[/latex] u cilindru.
Nap.: Koristim dvije različite fje [latex]d[/latex], jednu iz [latex]\mathbb{R}^2[/latex], a drugu iz [latex]\mathbb{R}^3[/latex], ali mislim da se skuži koja je koja. Neka vas to ne zbuni...
4. c) Da, fja ni u kojoj točkki [latex](2k, 0), k \in \mathbb{Z}[/latex] nema limes, a to se lako vidi izborom lijepih restrikcija, npr.
za [latex](2k, 0), k \neq 0, 2 \quad f(2k, y)[/latex] u limesu ode u beskonačnost;
za [latex](4, 0) \quad f(4, y) = 4[/latex] pa ide u 4, a [latex]f(x, 0) = 0[/latex] pa ide u 0;
za [latex](0, 0) \quad f(x, x)[/latex] i [latex]f(x, -x)[/latex] idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa [latex]x^2[/latex] i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa [latex]\frac{\sin{x}}{x}[/latex].
Možda može i ljepše, ali valjda će i ovo pomoći...
2007.
1. b) Neka je 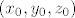 točka u cilindru. Onda je točka u cilindru. Onda je 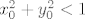 . .
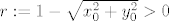 . Onda je za . Onda je za 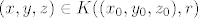
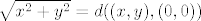
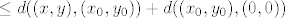
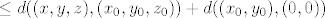
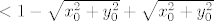
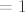
pa je 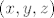 u cilindru. u cilindru.
Nap.: Koristim dvije različite fje 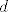 , jednu iz , jednu iz 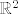 , a drugu iz , a drugu iz 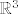 , ali mislim da se skuži koja je koja. Neka vas to ne zbuni... , ali mislim da se skuži koja je koja. Neka vas to ne zbuni...
4. c) Da, fja ni u kojoj točkki 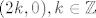 nema limes, a to se lako vidi izborom lijepih restrikcija, npr. nema limes, a to se lako vidi izborom lijepih restrikcija, npr.
za 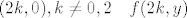 u limesu ode u beskonačnost; u limesu ode u beskonačnost;
za 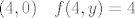 pa ide u 4, a pa ide u 4, a 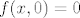 pa ide u 0; pa ide u 0;
za 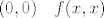 i i 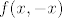 idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa 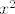 i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa 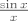 . .
Možda može i ljepše, ali valjda će i ovo pomoći...
|
|
| [Vrh] |
|
Gost
|
 Postano: 9:40 sri, 2. 11. 2011 Naslov: Postano: 9:40 sri, 2. 11. 2011 Naslov: |
    |
|
|
[quote="sz"]2007.
4. c) Da, fja ni u kojoj točkki [latex](2k, 0), k \in \mathbb{Z}[/latex] nema limes, a to se lako vidi izborom lijepih restrikcija, npr.
za [latex](2k, 0), k \neq 0, 2 \quad f(2k, y)[/latex] u limesu ode u beskonačnost;
za [latex](4, 0) \quad f(4, y) = 4[/latex] pa ide u 4, a [latex]f(x, 0) = 0[/latex] pa ide u 0;
za [latex](0, 0) \quad f(x, x)[/latex] i [latex]f(x, -x)[/latex] idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa [latex]x^2[/latex] i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa [latex]\frac{\sin{x}}{x}[/latex].
Možda može i ljepše, ali valjda će i ovo pomoći...[/quote]
a jel dovoljno samo pokazati da lim f(x,y) = beskonacno (kad (x,y) -> (2k,0))?
| sz (napisa): | 2007.
4. c) Da, fja ni u kojoj točkki 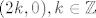 nema limes, a to se lako vidi izborom lijepih restrikcija, npr. nema limes, a to se lako vidi izborom lijepih restrikcija, npr.
za 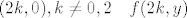 u limesu ode u beskonačnost; u limesu ode u beskonačnost;
za 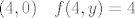 pa ide u 4, a pa ide u 4, a 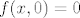 pa ide u 0; pa ide u 0;
za 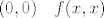 i i 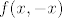 idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa idu u različite razlomke (samo tu treba malo srediti stvar da se ljepše vidi, tj. podijeliti brojnik i nazivnik sa 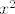 i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa i onda se ne zbuniti sa sinusom, nego ga lijepo naštimati na nešt tipa 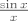 . .
Možda može i ljepše, ali valjda će i ovo pomoći... |
a jel dovoljno samo pokazati da lim f(x,y) = beskonacno (kad (x,y) → (2k,0))?
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 12:42 sri, 2. 11. 2011 Naslov: Postano: 12:42 sri, 2. 11. 2011 Naslov: |
    |
|
|
Kad bismo to uspjeli dokazati, bilo bi dovoljno, ali za (0, 0) i (4, 0) to nije istina (pa se ne može ni dokazati) (vidi se npr. po tome što ja gore uspjeh konstruirati nizove koji konvergiraju u (0, 0) i (4, 0), a čije funkcijske vrijednosti konvergiraju u nešto smisleno) pa za te točke ipak trebaš smisliti nešto drugo.
Kad bismo to uspjeli dokazati, bilo bi dovoljno, ali za (0, 0) i (4, 0) to nije istina (pa se ne može ni dokazati) (vidi se npr. po tome što ja gore uspjeh konstruirati nizove koji konvergiraju u (0, 0) i (4, 0), a čije funkcijske vrijednosti konvergiraju u nešto smisleno) pa za te točke ipak trebaš smisliti nešto drugo.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Jess
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (14:34:48)
Postovi: (2)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 18:48 sri, 2. 11. 2011 Naslov: Postano: 18:48 sri, 2. 11. 2011 Naslov: |
    |
|
|
Nikako! :D
Točke skupa A su i (1, 1, 0) i (1, 1, 56) i (1, 1, <bilo koji z>) - pa skup ne može biti ograničen. Slično i za skup B.
Caka je u tome da uvjeti kod skupova A i B, ''kače'' dvije dimenzije, a treću ''puštaju na miru''.
No zato će A presjek B imati uvjete na sve tri dimenzije! ;)
P.S. Ako je netko više vizualan tip, u xy-ravnini (kad je z = 0) skup A izgleda kao nekakva elipsa (tj. njegov rub izgleda kao elipsa, skup je ono unutar nje). Isto tako izgleda i kad je dignemo na z = 1, z = 2... znači kad ''razvučemo'' po osi z to izgleda kao nekakav cilindar.
Slično, u yz-ravnini (kad je x = 0) y^2 + z = 2 je parabola - koju opet ''razvučeš'' po x osi...
Nikako! 
Točke skupa A su i (1, 1, 0) i (1, 1, 56) i (1, 1, <bilo koji z>) - pa skup ne može biti ograničen. Slično i za skup B.
Caka je u tome da uvjeti kod skupova A i B, ''kače'' dvije dimenzije, a treću ''puštaju na miru''.
No zato će A presjek B imati uvjete na sve tri dimenzije! 
P.S. Ako je netko više vizualan tip, u xy-ravnini (kad je z = 0) skup A izgleda kao nekakva elipsa (tj. njegov rub izgleda kao elipsa, skup je ono unutar nje). Isto tako izgleda i kad je dignemo na z = 1, z = 2... znači kad ''razvučemo'' po osi z to izgleda kao nekakav cilindar.
Slično, u yz-ravnini (kad je x = 0) y^2 + z = 2 je parabola - koju opet ''razvučeš'' po x osi...
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
štangica
Forumaš(ica)
Pridružen/a: 19. 03. 2010. (17:18:17)
Postovi: (4C)16
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
|
| [Vrh] |
|
|








