|
[quote="*vz*"]Primjenom funkcija izvodnica rijesite rekurzivnu relaciju:
a_n+2 = 5a_n+1 - 4a_n; a_0 = 1; a_1 = 2
Funkcije izvodnice nismo još radili, pretpostavljam da se rješava po principu 15. zadatka, 111. str. iz Zbirke Cvitković. Ne razumijem na 112. str. zbrajanje po n element od N. Uvrstila sam za indexe i eksponente n=0,1,2 i nista pametno dobila. Također ne razumijem onaj korak nakon rastava na parcijalne razlomke te bih molila nekog dobre volje da mi objasni. Hvala :)[/quote]
nemam trenutno tu zbirku pa ne znam na koji zadatak tamo mislis, ali mogu ovako opcenito nesto reci. mozda :)
zbraja se po n iz N zato da dobijemo nesto sto slici na f(x), a f(x) smo pretpostavili da je u takvom obliku - sa sumom po n iz N
evo, ja sam cak rjesavala ovaj zadatak sad, i nakon tog sumiranja se dobije:
[latex](f(x)-a_0-a_1x)-5x(f(x)-a_0)+4x^2f(x)=0[/latex] jer u prvoj sumi fale prva dva clana od f(x) pa ih moramo oduzeti, u drugoj nakon sto izlucimo ispred x, fali prvi clan od f(x), a treca suma, nakon sto izlucimo x^2 je tocno jednaka f(x)
kad ovo malo sredimo, odnosno uvrstimo a_0 i a_1, i rastavimo na parcijalne razlomke, dobijemo:
[latex]f(x)=\frac{\frac{2}{3}}{1-x}+\frac{\frac{1}{3}}{1-4x}[/latex], odnosno [latex]f(x)=\frac{2}{3}\sum_{n\geq 0}x^n+\frac{1}{3}\sum_{n\geq 0} (4x)^n[/latex]
i sada samo preostaje ocitati sto stoji uz x^n jer to je upravo a_n (rastavljali smo na parcijalne razlomke zato da mozemo to ocitati)
znaci, rjesenje je [latex]a_n=\frac{2}{3}+\frac{1}{3}\cdot 4^n[/latex]
| *vz* (napisa): | Primjenom funkcija izvodnica rijesite rekurzivnu relaciju:
a_n+2 = 5a_n+1 - 4a_n; a_0 = 1; a_1 = 2
Funkcije izvodnice nismo još radili, pretpostavljam da se rješava po principu 15. zadatka, 111. str. iz Zbirke Cvitković. Ne razumijem na 112. str. zbrajanje po n element od N. Uvrstila sam za indexe i eksponente n=0,1,2 i nista pametno dobila. Također ne razumijem onaj korak nakon rastava na parcijalne razlomke te bih molila nekog dobre volje da mi objasni. Hvala  |
nemam trenutno tu zbirku pa ne znam na koji zadatak tamo mislis, ali mogu ovako opcenito nesto reci. mozda 
zbraja se po n iz N zato da dobijemo nesto sto slici na f(x), a f(x) smo pretpostavili da je u takvom obliku - sa sumom po n iz N
evo, ja sam cak rjesavala ovaj zadatak sad, i nakon tog sumiranja se dobije:
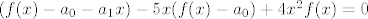 jer u prvoj sumi fale prva dva clana od f(x) pa ih moramo oduzeti, u drugoj nakon sto izlucimo ispred x, fali prvi clan od f(x), a treca suma, nakon sto izlucimo x^2 je tocno jednaka f(x) jer u prvoj sumi fale prva dva clana od f(x) pa ih moramo oduzeti, u drugoj nakon sto izlucimo ispred x, fali prvi clan od f(x), a treca suma, nakon sto izlucimo x^2 je tocno jednaka f(x)
kad ovo malo sredimo, odnosno uvrstimo a_0 i a_1, i rastavimo na parcijalne razlomke, dobijemo:
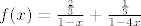 , odnosno , odnosno 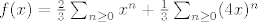
i sada samo preostaje ocitati sto stoji uz x^n jer to je upravo a_n (rastavljali smo na parcijalne razlomke zato da mozemo to ocitati)
znaci, rjesenje je 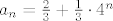
_________________
Nov, još gluplji.
|





