| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
|
| [Vrh] |
|
ddujmic
Forumaš(ica)

Pridružen/a: 17. 02. 2009. (14:01:31)
Postovi: (75)16
|
|
| [Vrh] |
|
ddz
Forumaš(ica)

Pridružen/a: 29. 10. 2004. (22:49:49)
Postovi: (4D)16
Spol: 
|
 Postano: 15:10 uto, 8. 11. 2011 Naslov: Kolokvij 06.11.2009 zadatak 4. Postano: 15:10 uto, 8. 11. 2011 Naslov: Kolokvij 06.11.2009 zadatak 4. |
    |
|
|
Kolokvij 06.11.2009 zadatak 4.
Mogu li iz činjenice da je [latex]\pi[/latex] hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od [latex]\pi + {T}[/latex] jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1.
Kolokvij 06.11.2009 zadatak 4.
Mogu li iz činjenice da je  hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od 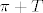 jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1. jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1.
_________________
oldičan datkilgoraf tržai posoa, pšiem perko 010 rjieič um inuti, saom se jaivte ardi dogovroa an 0998030117. HVAAL NA POJVEREJNU!!1
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 15:40 uto, 8. 11. 2011 Naslov: Re: Kolokvij 06.11.2009 zadatak 4. Postano: 15:40 uto, 8. 11. 2011 Naslov: Re: Kolokvij 06.11.2009 zadatak 4. |
    |
|
|
[quote="ddz"]Kolokvij 06.11.2009 zadatak 4.
Mogu li iz činjenice da je [latex]\pi[/latex] hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od [latex]\pi + {T}[/latex] jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1.[/quote]
Da i da :)
U grupi A je dimenzija od [tex]\Pi + \{T\}[/tex] jednaka 4 jer [tex]T \notin \Pi[/tex], a u grupi B je dimenzija 3 jer je [tex]T \in \Pi[/tex].
| ddz (napisa): | Kolokvij 06.11.2009 zadatak 4.
Mogu li iz činjenice da je  hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od hiperravnina i da točka [tex]T \notin \pi[/tex] zaključiti da je dimenzija od 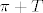 jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1. jednaka dimenziji prostora, tj. 4? Tj, općenito, ako točka pripada ravnini dimenzija ravnine se ne mijenja, inače se dimenzija povećava za 1. |
Da i da 
U grupi A je dimenzija od [tex]\Pi + \{T\}[/tex] jednaka 4 jer [tex]T \notin \Pi[/tex], a u grupi B je dimenzija 3 jer je [tex]T \in \Pi[/tex].
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 20:50 uto, 8. 11. 2011 Naslov: Postano: 20:50 uto, 8. 11. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]http://web.math.hr/nastava/eukl/ZAD_12.pdf
Jel bi se nekom dalo rijesit prvi pod c d i e. hvaalaaa:)[/quote]
ovdje je i 1.b) krivi, to sam već ranije spomenuo, pa mi nitko nije potvrdio, ali to ne može biti afin prostor. imamo i u c) i d) dijelu zadatka prostore A i V različitih dimenzija, pa ni tu nisu u pitanju afini prostori, evo postupak:
1.c) [latex]\forall (x_1,y_1) \in \mathcal{A} \quad \forall (a,b,c) \in V \quad \exists ! (x_2,y_2) \in \mathcal{A} \quad td \quad v((x_1,y_1),(x_2,y_2)) = (a,b,c)[/latex]
[latex](x_2-x_1,y_2-y_1,0) = (a,b,c) \Rightarrow c=0, \forall c \in \mathbb{R}[/latex]
Očito ne vrijedi za svaki realni broj da je jednak nuli, pa svojstvo A1 ne vrijedi.
1.d) Nakon sličnog raspisivanja kao u gornjem zadatku, dobije se
[latex](x_2-x_1+y_2-y_1,z_2-z_1) = (a,b)[/latex]
[latex]\Rightarrow x_2+y_2 = x_1+y_1+a[/latex]
i nemamo više uvjeta na [latex]x_2[/latex] i [latex]y_2[/latex], pa beskonačno mnogo uređenih parova [latex](x_2,y_2)[/latex] zadovoljavaju gornju jednakost, dakle ne vrijedi A1.
1.e) Uzmimo proizvoljnu [latex]f\colon [0,1] \rightarrow \mathbb{R}[/latex] i proizvoljni [latex]x\in \mathbb{R}[/latex], treba pokazati da postoji jedinstvena [latex]g\colon [0,1] \rightarrow \mathbb{R}[/latex] takva da je [latex]v(f,g)=x[/latex].
Imamo [latex]v(f,g) = f(0)-g(0)=x \Rightarrow g(0)=f(0)-x[/latex], dakle definirali smo funkciju [latex]g[/latex] samo u nuli. Očito možemo definirati beskonačno mnogo neprekidnih funkcija sa [latex] [0,1] [/latex] u [latex] \mathbb{R} [/latex] koje su tako definirane u nuli. Drugim riječima, za svaku točku [latex]A \in \mathcal{A}[/latex] i [latex]x \in V[/latex] postoji beskonačno mnogo točaka [latex]B \in \mathcal{A}[/latex] koje zadovoljavaju [latex]v(A,B)=x[/latex].
edit: ne radi latex, ako netko skuži zašto, molim neka viče :?
edit^2: pisao sam \tex umjesto /tex :D
| Anonymous (napisa): | http://web.math.hr/nastava/eukl/ZAD_12.pdf
Jel bi se nekom dalo rijesit prvi pod c d i e. hvaalaaa:) |
ovdje je i 1.b) krivi, to sam već ranije spomenuo, pa mi nitko nije potvrdio, ali to ne može biti afin prostor. imamo i u c) i d) dijelu zadatka prostore A i V različitih dimenzija, pa ni tu nisu u pitanju afini prostori, evo postupak:
1.c) 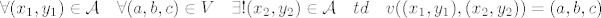
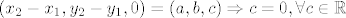
Očito ne vrijedi za svaki realni broj da je jednak nuli, pa svojstvo A1 ne vrijedi.
1.d) Nakon sličnog raspisivanja kao u gornjem zadatku, dobije se
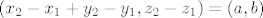
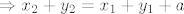
i nemamo više uvjeta na 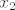 i i 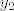 , pa beskonačno mnogo uređenih parova , pa beskonačno mnogo uređenih parova 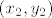 zadovoljavaju gornju jednakost, dakle ne vrijedi A1. zadovoljavaju gornju jednakost, dakle ne vrijedi A1.
1.e) Uzmimo proizvoljnu  i proizvoljni i proizvoljni 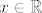 , treba pokazati da postoji jedinstvena , treba pokazati da postoji jedinstvena 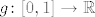 takva da je takva da je 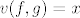 . .
Imamo 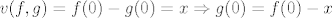 , dakle definirali smo funkciju , dakle definirali smo funkciju  samo u nuli. Očito možemo definirati beskonačno mnogo neprekidnih funkcija sa samo u nuli. Očito možemo definirati beskonačno mnogo neprekidnih funkcija sa 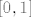 u u 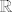 koje su tako definirane u nuli. Drugim riječima, za svaku točku koje su tako definirane u nuli. Drugim riječima, za svaku točku 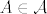 i i 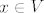 postoji beskonačno mnogo točaka postoji beskonačno mnogo točaka 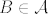 koje zadovoljavaju koje zadovoljavaju  . .
edit: ne radi latex, ako netko skuži zašto, molim neka viče 
edit^2: pisao sam \tex umjesto /tex 
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 23:07 uto, 8. 11. 2011 Naslov: Postano: 23:07 uto, 8. 11. 2011 Naslov: |
    |
|
|
[quote="lost_soul"]može mala pomoć oko 2. zadatka iz prošle godine, prva grupa? :?[/quote]
Ja imam samo jednu grupu, pa ću pretpostaviti da je to ovaj zadatak: [latex]A,B,C \in \pi, \quad T \in \mathcal{A} \quad i \quad \overrightarrow{AT}=\overrightarrow{BC}+\frac{1}{2} \overrightarrow{AC} \quad [/latex] i treba pokazati [latex]T \in \pi[/latex].
Jedino što mi je palo na pamet ovdje je da kažemo da je [latex]W[/latex] pripadni vektorski prostor ravnine [latex]\pi[/latex] i iskoristimo to što su [latex]\overrightarrow{BC}, \overrightarrow{AC} \in W[/latex], pa je desna strana dane jednakosti kao zbroj dva vektora iz [latex]W[/latex] sadržana u [latex]W[/latex]. Stoga mora i lijeva strana jednakosti biti sadržana u [latex]W[/latex], iz čega slijedi [latex]\overrightarrow{AT} \in W[/latex], odnosno [latex]T \in \pi[/latex].
| lost_soul (napisa): | može mala pomoć oko 2. zadatka iz prošle godine, prva grupa?  |
Ja imam samo jednu grupu, pa ću pretpostaviti da je to ovaj zadatak: 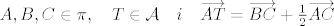 i treba pokazati i treba pokazati 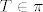 . .
Jedino što mi je palo na pamet ovdje je da kažemo da je 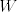 pripadni vektorski prostor ravnine pripadni vektorski prostor ravnine  i iskoristimo to što su i iskoristimo to što su 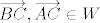 , pa je desna strana dane jednakosti kao zbroj dva vektora iz , pa je desna strana dane jednakosti kao zbroj dva vektora iz 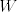 sadržana u sadržana u 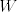 . Stoga mora i lijeva strana jednakosti biti sadržana u . Stoga mora i lijeva strana jednakosti biti sadržana u 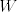 , iz čega slijedi , iz čega slijedi  , odnosno , odnosno 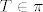 . .
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
sparkle_
Forumaš(ica)

Pridružen/a: 13. 02. 2011. (11:08:40)
Postovi: (E)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 22:09 ned, 15. 1. 2012 Naslov: Postano: 22:09 ned, 15. 1. 2012 Naslov: |
    |
|
|
[quote="sparkle_"]S obzirom da sam bila bolesna pa cijeli prosinac nisam isla na predavanja i vjezbe, moze li mi netko molim vas reci do kuda smo dosli sa vjezbama iz euklidskih tj do kuda pisemo kolokvij?
I da li ce kolokvij opet biti na zaokruzivanje ili?
Hvala puno[/quote]
one vježbe šta imaš na netu smo sve napravili.
da, opet na zaokruživanje, al će bit ponuđen samo 1 točan odgovor i bit će negativnih bodova, mislim -0,5
| sparkle_ (napisa): | S obzirom da sam bila bolesna pa cijeli prosinac nisam isla na predavanja i vjezbe, moze li mi netko molim vas reci do kuda smo dosli sa vjezbama iz euklidskih tj do kuda pisemo kolokvij?
I da li ce kolokvij opet biti na zaokruzivanje ili?
Hvala puno |
one vježbe šta imaš na netu smo sve napravili.
da, opet na zaokruživanje, al će bit ponuđen samo 1 točan odgovor i bit će negativnih bodova, mislim -0,5
|
|
| [Vrh] |
|
bigBADdaddy
Gost
|
|
| [Vrh] |
|
|









