| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 21:00 pon, 29. 3. 2010 Naslov: 3 b) zadatak sa kolokvija 08/09 Postano: 21:00 pon, 29. 3. 2010 Naslov: 3 b) zadatak sa kolokvija 08/09 |
    |
|
|
Na današnijm demonstraturama sam ostao dužan jedan zadatak, pa u nastavku slijedi njegovo rješenje. Radi se o 3 b) zadatku sa prošlogodišnjeg kolokvija. Nadam se da će još nekima ovo biti od koristi :)
Odredite [latex]Int(\mathbb{Z} \oplus \mathbb{Z})[/latex] i [latex]Aut(\mathbb{Z} \oplus \mathbb{Z})[/latex]. Jesu li te grupe cikličke?
Prvi dio je jednostavan. Za svaku komutativnu grupu, pa specijalno i za [latex]\mathbb{Z} \oplus \mathbb{Z}[/latex] vrijedi [latex]Int(G) = \{ id_G \}[/latex]. Jasno da je ta ciklička.
Sad automorfizmi. Znamo da je [latex]\mathbb{Z} \oplus \mathbb{Z} = \langle (1,0), (0,1) \rangle[/latex] pa je dovoljno vidjeti kamo se preslikaju generatori. Slike svih ostalih dobijemo proširenjem po pravilu koje zadovoljavaju homomorfizmi. Uočimo sada da svaki automorfizam možemo predstaviti nekom matricom iz [latex]M_2(\mathbb{Z})[/latex]. Ako je [latex]f(1,0)=(a,c)[/latex], a [latex]f(0,1)=(b,d)[/latex] onda je dani automorfizam predstavljen sa
[latex]\left( \begin{array}{cc}
a & b \\
c & d \end{array} \right)[/latex]
No je li svaka takva matrica dobra? Da li za proizvoljne [latex]a, b, c, d \in \mathbb{Z}[/latex] vrijedi da linearno preslikavanje A definira jedan automorfizam na [latex]\mathbb{Z} \oplus \mathbb{Z}[/latex]? Odgovor je (već pogađate) - ne! Naime jasno je da čim imam singularnu matricu njena slika neće biti čitav [latex]\mathbb{Z} \oplus \mathbb{Z}[/latex]. Odnosno svi elementi iz slike će biti međusobno proporcionalni. Dakle matrica mora biti regularna, odnosno mora biti [latex]ad-bc \neq 0[/latex] . Ali ni to nije sve. Ako je nešto automorfizam onda je bijekcija. Kako biti siguran da će regularna matrica pogoditi sve vrijednosti iz [latex]\mathbb{Z} \oplus \mathbb{Z}[/latex]. Na vektorskom prostoru [latex]\mathbb{R}^2[/latex] to vrijedi ali mi ovdje radimo samo s cijelim brojevima. Da bi bili sigurni da su svi elementi iz [latex]\mathbb{Z} \oplus \mathbb{Z}[/latex] pogođeni, moramo za svaki [latex]\left( \begin{array}{c} x \\ y \end{array} \right)[/latex] naći vektor [latex]\left( \begin{array}{c} u \\ v \end{array} \right)[/latex] koji se u njega preslika, tj. za kojeg vrijedi
[latex]\left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{cc}
a & b \\
c & d \end{array} \right) \left( \begin{array}{c} u \\ v \end{array} \right)[/latex]
Sve su gore cijeli brojevi. Ali mi znamo naći taj [latex]\left( \begin{array}{c} u \\ v \end{array} \right)[/latex]. On će biti
[latex]\frac{1}{ad-bc} \left( \begin{array}{cc}
d & -b \\
-c & a \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)[/latex]
Tu sam iskoristio poznatu formulu za inverz 2x2 matrice. Ali problem je da li je to što dobijemo par cijelih brojeva. Štoviše to mora biti par cijelih brojeva za koje god [latex]\left( \begin{array}{c} x \\ y \end{array} \right)[/latex] to promatrali. Specijalno i za [latex]\left( \begin{array}{c} 1 \\ 0 \end{array} \right)[/latex] i [latex]\left( \begin{array}{c} 0 \\ 1 \end{array} \right)[/latex] . Dakle inverz mora bit iz [latex]M_2(\mathbb{Z})[/latex] i to je dovoljno. Ali sad pogledamo što imamo i vidimo da onda mora biti [latex](ad-bc) | a ,\: (ad-bc) | b ,\: (ad-bc) | c[/latex] i [latex](ad-bc) | d[/latex] . No iz toga slijedi da [latex](ad-bc)^2 | (ad-bc)[/latex] . Jedini način da kvadrat cijelog broja djeli sebe samog jest da je taj cijeli broj +1 ili -1. Konačno, rješenje je [latex]Aut(\mathbb{Z} \oplus \mathbb{Z}) \cong \{ A \in M_2(\mathbb{Z}) : \det A = \pm 1 \}[/latex] . Još pitanje o cikličnosti. Ova grupa nije ciklička, jer kad bi bila generirana jednim elementom A, onda bi (budući je matrica [latex]M =
\left( \begin{array}{cc}
-1 & 0 \\
0 & -1 \end{array} \right)[/latex] unutra) moralo vrijediti da je [latex]A^n = M[/latex] , za neki [latex]n \in \mathbb{Z} , n \neq 0 [/latex]. Ali tada bi [latex]A^{2n} = I[/latex] , pa bi imali da je gornja grupa konačna što nije!
Usporedite sa modularnom grupom koja je spomenuta na predavanjima ([url=http://web.math.hr/nastava/alg/predavanja/ASpred.pdf]skripta[/url] str. 16)
3 b) zadatak iz druge grupe je (po mojoj procjeni) jednostavniji pa ga ostavljam vama za vježbu :D
Na današnijm demonstraturama sam ostao dužan jedan zadatak, pa u nastavku slijedi njegovo rješenje. Radi se o 3 b) zadatku sa prošlogodišnjeg kolokvija. Nadam se da će još nekima ovo biti od koristi 
Odredite 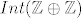 i i 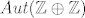 . Jesu li te grupe cikličke? . Jesu li te grupe cikličke?
Prvi dio je jednostavan. Za svaku komutativnu grupu, pa specijalno i za  vrijedi vrijedi 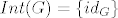 . Jasno da je ta ciklička. . Jasno da je ta ciklička.
Sad automorfizmi. Znamo da je 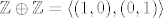 pa je dovoljno vidjeti kamo se preslikaju generatori. Slike svih ostalih dobijemo proširenjem po pravilu koje zadovoljavaju homomorfizmi. Uočimo sada da svaki automorfizam možemo predstaviti nekom matricom iz pa je dovoljno vidjeti kamo se preslikaju generatori. Slike svih ostalih dobijemo proširenjem po pravilu koje zadovoljavaju homomorfizmi. Uočimo sada da svaki automorfizam možemo predstaviti nekom matricom iz 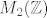 . Ako je . Ako je 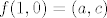 , a , a 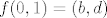 onda je dani automorfizam predstavljen sa onda je dani automorfizam predstavljen sa
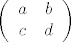
No je li svaka takva matrica dobra? Da li za proizvoljne 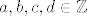 vrijedi da linearno preslikavanje A definira jedan automorfizam na vrijedi da linearno preslikavanje A definira jedan automorfizam na  ? Odgovor je (već pogađate) - ne! Naime jasno je da čim imam singularnu matricu njena slika neće biti čitav ? Odgovor je (već pogađate) - ne! Naime jasno je da čim imam singularnu matricu njena slika neće biti čitav  . Odnosno svi elementi iz slike će biti međusobno proporcionalni. Dakle matrica mora biti regularna, odnosno mora biti . Odnosno svi elementi iz slike će biti međusobno proporcionalni. Dakle matrica mora biti regularna, odnosno mora biti 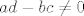 . Ali ni to nije sve. Ako je nešto automorfizam onda je bijekcija. Kako biti siguran da će regularna matrica pogoditi sve vrijednosti iz . Ali ni to nije sve. Ako je nešto automorfizam onda je bijekcija. Kako biti siguran da će regularna matrica pogoditi sve vrijednosti iz  . Na vektorskom prostoru . Na vektorskom prostoru 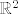 to vrijedi ali mi ovdje radimo samo s cijelim brojevima. Da bi bili sigurni da su svi elementi iz to vrijedi ali mi ovdje radimo samo s cijelim brojevima. Da bi bili sigurni da su svi elementi iz  pogođeni, moramo za svaki pogođeni, moramo za svaki 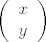 naći vektor naći vektor 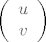 koji se u njega preslika, tj. za kojeg vrijedi koji se u njega preslika, tj. za kojeg vrijedi
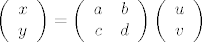
Sve su gore cijeli brojevi. Ali mi znamo naći taj 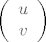 . On će biti . On će biti
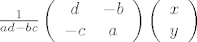
Tu sam iskoristio poznatu formulu za inverz 2x2 matrice. Ali problem je da li je to što dobijemo par cijelih brojeva. Štoviše to mora biti par cijelih brojeva za koje god 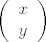 to promatrali. Specijalno i za to promatrali. Specijalno i za 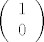 i i 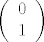 . Dakle inverz mora bit iz . Dakle inverz mora bit iz 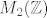 i to je dovoljno. Ali sad pogledamo što imamo i vidimo da onda mora biti i to je dovoljno. Ali sad pogledamo što imamo i vidimo da onda mora biti 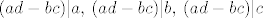 i i 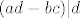 . No iz toga slijedi da . No iz toga slijedi da 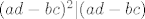 . Jedini način da kvadrat cijelog broja djeli sebe samog jest da je taj cijeli broj +1 ili -1. Konačno, rješenje je . Jedini način da kvadrat cijelog broja djeli sebe samog jest da je taj cijeli broj +1 ili -1. Konačno, rješenje je 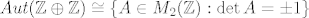 . Još pitanje o cikličnosti. Ova grupa nije ciklička, jer kad bi bila generirana jednim elementom A, onda bi (budući je matrica . Još pitanje o cikličnosti. Ova grupa nije ciklička, jer kad bi bila generirana jednim elementom A, onda bi (budući je matrica  unutra) moralo vrijediti da je unutra) moralo vrijediti da je 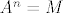 , za neki , za neki 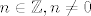 . Ali tada bi . Ali tada bi 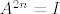 , pa bi imali da je gornja grupa konačna što nije! , pa bi imali da je gornja grupa konačna što nije!
Usporedite sa modularnom grupom koja je spomenuta na predavanjima (skripta str. 16)
3 b) zadatak iz druge grupe je (po mojoj procjeni) jednostavniji pa ga ostavljam vama za vježbu 
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
piper at the gates
Forumaš(ica)

Pridružen/a: 14. 03. 2009. (20:02:03)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
there is no spoon
Forumaš(ica)

Pridružen/a: 11. 04. 2008. (11:12:06)
Postovi: (36)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
MARKOOO123
Forumaš(ica)

Pridružen/a: 28. 12. 2011. (19:49:08)
Postovi: (3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Robica
Forumaš(ica)

Pridružen/a: 11. 12. 2011. (21:45:03)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
kranjčević
Forumaš(ica)

Pridružen/a: 15. 04. 2012. (12:34:44)
Postovi: (15)16
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
 Postano: 18:33 uto, 16. 4. 2013 Naslov: Postano: 18:33 uto, 16. 4. 2013 Naslov: |
    |
|
|
Demonstrature iz Algebarskih struktura za nastavnički smjer za ovaj semestar napokon počinju.
Održavat će se [b]četvrtkom[/b] [b]od 10:15 do 12 sati[/b]. Najava je [b]obvezna[/b] na hrvoje.stojanovic [at] student.math.hr (ili nekako već, npr. uživo). U slučaju da se netko najavi čekat ću pred oglasnom pločom. Također, slobodno možete poslati pitanje/zadatak na mail, a ja ću se potruditi što prije odgovoriti.
Ukoliko imate neko predavanje/vježbe u ponuđenom terminu, javite se pa ćemo se dogovoriti za neki drugi. Za vrijeme kolokvijskih tjedana demonstrature se neće održavati, a ako bude potrebno javite se pa ćemo nešto smisliti.
EDIT: promjena termina
Demonstrature iz Algebarskih struktura za nastavnički smjer za ovaj semestar napokon počinju.
Održavat će se četvrtkom od 10:15 do 12 sati. Najava je obvezna na hrvoje.stojanovic [at] student.math.hr (ili nekako već, npr. uživo). U slučaju da se netko najavi čekat ću pred oglasnom pločom. Također, slobodno možete poslati pitanje/zadatak na mail, a ja ću se potruditi što prije odgovoriti.
Ukoliko imate neko predavanje/vježbe u ponuđenom terminu, javite se pa ćemo se dogovoriti za neki drugi. Za vrijeme kolokvijskih tjedana demonstrature se neće održavati, a ako bude potrebno javite se pa ćemo nešto smisliti.
EDIT: promjena termina
Zadnja promjena: hstojanovic; 21:13 sri, 17. 4. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
plz
Gost
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
|
















