| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 16:23 sri, 29. 2. 2012 Naslov: Postano: 16:23 sri, 29. 2. 2012 Naslov: |
    |
|
|
Vidim da je Phoenix odgovorio, no svejedno postam, zbog sitne tehnikalije.
Pretpostavi da A nije surjekcija, tj. postoji [tex]y_1[/tex] takav da je [tex]Ax \ne y_1[/tex] za svaki x. Tada mozes [tex]y_1[/tex] nadopuniti do baze prostora: [tex]\{y_1, \dots, y_n\}[/tex]. Sada definiraj [tex]By_1 = z \ne 0[/tex] i [tex]By_i = 0, i > 1[/tex] (linearni operator je dosta definirati djelovanjem na bazi). Primijeti da je slika od A podskup prostora razapetog skupom [tex]\{y_{\bf 2}, \dots, y_n\}[/tex], sto znaci da je [tex]B(A(x)) = 0[/tex] jednako nuli za svaki x, a B nije nul-operator.
Dakle, slicno Pheonixu, uz sitan detalj: formalno je B ovdje bolje definiran (na bazi), dok kod Phoenixa nije [i]a priori[/i] ocito da je definiran linearni operator. Do na taj detalj, rjesenja su nam ekvivalentna.
Vidim da je Phoenix odgovorio, no svejedno postam, zbog sitne tehnikalije.
Pretpostavi da A nije surjekcija, tj. postoji [tex]y_1[/tex] takav da je [tex]Ax \ne y_1[/tex] za svaki x. Tada mozes [tex]y_1[/tex] nadopuniti do baze prostora: [tex]\{y_1, \dots, y_n\}[/tex]. Sada definiraj [tex]By_1 = z \ne 0[/tex] i [tex]By_i = 0, i > 1[/tex] (linearni operator je dosta definirati djelovanjem na bazi). Primijeti da je slika od A podskup prostora razapetog skupom [tex]\{y_{\bf 2}, \dots, y_n\}[/tex], sto znaci da je [tex]B(A(x)) = 0[/tex] jednako nuli za svaki x, a B nije nul-operator.
Dakle, slicno Pheonixu, uz sitan detalj: formalno je B ovdje bolje definiran (na bazi), dok kod Phoenixa nije a priori ocito da je definiran linearni operator. Do na taj detalj, rjesenja su nam ekvivalentna.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
 Postano: 18:28 pet, 2. 3. 2012 Naslov: Postano: 18:28 pet, 2. 3. 2012 Naslov: |
    |
|
|
da ne otvaram novu temu
http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0506-kol1a.pdf
3. zad
ako može netko, kako da dobijem dualnu bazu
tj. muči me to što nikako ne mogu prikazat proizvoljnu matricu u zadanoj bazi
tj. ako je matrica A:
a b
c d
a baza e1, e2, e3, e4
A=alfa*e1+beta*e2+gama*e3+delta*e4
i sad nikako ne uspjevam izrazit alfa, beta, gama i delta pomoću a, b, c i d,
ostaje mi u prikazu beta?!?!
pliz pomoć
hvala
da ne otvaram novu temu
http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0506-kol1a.pdf
3. zad
ako može netko, kako da dobijem dualnu bazu
tj. muči me to što nikako ne mogu prikazat proizvoljnu matricu u zadanoj bazi
tj. ako je matrica A:
a b
c d
a baza e1, e2, e3, e4
A=alfa*e1+beta*e2+gama*e3+delta*e4
i sad nikako ne uspjevam izrazit alfa, beta, gama i delta pomoću a, b, c i d,
ostaje mi u prikazu beta?!?!
pliz pomoć
hvala
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 22:56 pet, 2. 3. 2012 Naslov: Postano: 22:56 pet, 2. 3. 2012 Naslov: |
    |
|
|
Primijeti da se u zadatku ne trazi od tebe da eksplicitno napises dualnu bazu, nego samo da prikazes [latex]f^*[/latex] preko nje. Kako je [latex]f^*(A) = tr(AX)[/latex], dobije se da je u biti
[latex]f^*( \left( \begin{array}{ccc}
a & b\\
c & d \end{array} \right) ) = c- b [/latex]. Sad, oznacimo ovu danu bazu sa [latex]\{A_1,A_2,A_3,A_4\}[/latex], i njoj dualnu bazu sa [latex]\{A_1^*,A_2^*,A_3^*,A_4^*\}[/latex]. Sad [latex]f^* = \alpha _1A_1^* + \alpha _2A_2^* + \alpha _3A_3^* + \alpha _4A_4^*\\[/latex]. Uvrstimo u ovu jednadzbu redom [latex]A_1,A_2,A_3,A_4[/latex] i dobijemo
[latex]
\alpha _1 = f^*(A_1) = -1 -1 = -2 \\
\alpha _2 = f^*(A_2) = 3-2 =1 \\
\alpha _3 = f^*(A_3) = 2-1 = 1 \\
\alpha _4 = f^*(A_4) = 4-1 = 3 \\ [/latex]
pa je [latex]f^* = -2A_1^* + A_2^* + A_3^* + 3A_4^*\\[/latex]
Ako te bas zanima eksplicitno odrediti elemente ove dualne baze, onda npr. za [latex]A_1^*[/latex] napises [latex] A_1^*(\left( \begin{array}{ccc}
a & b\\
c & d \end{array} \right) ) = \alpha a + \beta b + \gamma c + \delta d [/latex] pa uvrstis [latex]A_1,A_2,A_3,A_4[/latex] (pri cemu je [latex]A_1^*(A_1) = 1, A_1^*(A_2)=A_1^*(A_3)=A_1^*(A_4)=0[/latex]) i nades [latex]\alpha , \beta, \gamma , \delta [/latex] iz dobivenog 4x4 sustava. Onda sve to za [latex]A_2^*,A_3^*,A_4^*[/latex]. Ali, kako sam rekao, to se ne trazi u zadatku 8)
Primijeti da se u zadatku ne trazi od tebe da eksplicitno napises dualnu bazu, nego samo da prikazes 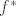 preko nje. Kako je preko nje. Kako je 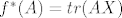 , dobije se da je u biti , dobije se da je u biti
 . Sad, oznacimo ovu danu bazu sa . Sad, oznacimo ovu danu bazu sa 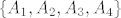 , i njoj dualnu bazu sa , i njoj dualnu bazu sa 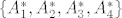 . Sad . Sad 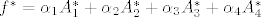 . Uvrstimo u ovu jednadzbu redom . Uvrstimo u ovu jednadzbu redom 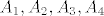 i dobijemo i dobijemo

pa je 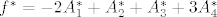
Ako te bas zanima eksplicitno odrediti elemente ove dualne baze, onda npr. za 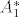 napises napises 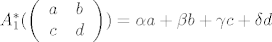 pa uvrstis pa uvrstis 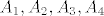 (pri cemu je (pri cemu je 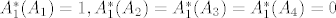 ) i nades ) i nades 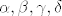 iz dobivenog 4x4 sustava. Onda sve to za iz dobivenog 4x4 sustava. Onda sve to za 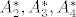 . Ali, kako sam rekao, to se ne trazi u zadatku . Ali, kako sam rekao, to se ne trazi u zadatku 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 18:04 čet, 8. 3. 2012 Naslov: Postano: 18:04 čet, 8. 3. 2012 Naslov: |
    |
|
|
Evo a) podzadatak, a b) ide slicno...
Neka je [tex](p) = \{p_1, p_2\}[/tex] baza za [tex]P_1[/tex] takva da je
[dtex][A]_p^p = \begin{bmatrix} \frac{4}{3} & \frac{2}{3} \\ \frac{1}{3} & \frac{5}{3} \end{bmatrix}[/dtex]
Iz definicije operatora [tex]A[/tex] imamo:
[dtex]A(p_1)(t) = tp_1'(t) + p_1(t)[/dtex]
[dtex]A(p_2)(t) = tp_2'(t) + p_2(t)[/dtex]
A iz matricnog zapisa:
[dtex]A(p_1)(t) = \frac{4}{3}p_1(t) + \frac{1}{3}p_2(t)[/dtex]
[dtex]A(p_2)(t) = \frac{2}{3}p_1(t) + \frac{5}{3}p_2(t)[/dtex]
Iz ovoga dobivamo sustav jednadzbi:
[dtex]tp_1'(t) + p_1(t) = \frac{4}{3}p_1(t) + \frac{1}{3}p_2(t) \Rightarrow tp_1'(t)= \frac{1}{3}p_1(t) + \frac{1}{3}p_2(t)[/dtex]
[dtex]tp_2'(t) + p_2(t) = \frac{2}{3}p_1(t) + \frac{5}{3}p_2(t) \Rightarrow tp_2'(t)= \frac{2}{3}p_1(t) + \frac{2}{3}p_2(t)[/dtex]
[tex]p_1[/tex] i [tex]p_2[/tex] su polinomi prvog stupnja pa se mogu zapisati u obliku: [tex]p_1(t) = a_1t + b_1[/tex] i [tex]p_2(t) = a_2t + b_2[/tex].
Uvrstavanjem u gornji sustav dobivamo:
[dtex]ta_1= \frac{1}{3}(a_1t + b_1) + \frac{1}{3}(a_2t + b_2)[/dtex]
[dtex]ta_2= \frac{2}{3}(a_1t + b_1) + \frac{2}{3}(a_2t + b_2)[/dtex]
Kada se to rijesi dobije se:
[dtex] a_2 = 2a_1[/dtex]
[dtex] b_2 = -b_1[/dtex]
Trazi se samo jedna baza pa mozemo uzeti npr. [tex]a_1 = 1, \ b_1 = 1[/tex] (samo treba paziti da su [tex]p_1[/tex] i [tex]p_2[/tex] linearno nezavisni),
pa je jedno rjesenje: [tex](p) = \{t + 1, 2t - 1\}[/tex]
Evo a) podzadatak, a b) ide slicno...
Neka je [tex](p) = \{p_1, p_2\}[/tex] baza za [tex]P_1[/tex] takva da je
[dtex][A]_p^p = \begin{bmatrix} \frac{4}{3} & \frac{2}{3} \\ \frac{1}{3} & \frac{5}{3} \end{bmatrix}[/dtex]
Iz definicije operatora [tex]A[/tex] imamo:
[dtex]A(p_1)(t) = tp_1'(t) + p_1(t)[/dtex]
[dtex]A(p_2)(t) = tp_2'(t) + p_2(t)[/dtex]
A iz matricnog zapisa:
[dtex]A(p_1)(t) = \frac{4}{3}p_1(t) + \frac{1}{3}p_2(t)[/dtex]
[dtex]A(p_2)(t) = \frac{2}{3}p_1(t) + \frac{5}{3}p_2(t)[/dtex]
Iz ovoga dobivamo sustav jednadzbi:
[dtex]tp_1'(t) + p_1(t) = \frac{4}{3}p_1(t) + \frac{1}{3}p_2(t) \Rightarrow tp_1'(t)= \frac{1}{3}p_1(t) + \frac{1}{3}p_2(t)[/dtex]
[dtex]tp_2'(t) + p_2(t) = \frac{2}{3}p_1(t) + \frac{5}{3}p_2(t) \Rightarrow tp_2'(t)= \frac{2}{3}p_1(t) + \frac{2}{3}p_2(t)[/dtex]
[tex]p_1[/tex] i [tex]p_2[/tex] su polinomi prvog stupnja pa se mogu zapisati u obliku: [tex]p_1(t) = a_1t + b_1[/tex] i [tex]p_2(t) = a_2t + b_2[/tex].
Uvrstavanjem u gornji sustav dobivamo:
[dtex]ta_1= \frac{1}{3}(a_1t + b_1) + \frac{1}{3}(a_2t + b_2)[/dtex]
[dtex]ta_2= \frac{2}{3}(a_1t + b_1) + \frac{2}{3}(a_2t + b_2)[/dtex]
Kada se to rijesi dobije se:
[dtex] a_2 = 2a_1[/dtex]
[dtex] b_2 = -b_1[/dtex]
Trazi se samo jedna baza pa mozemo uzeti npr. [tex]a_1 = 1, \ b_1 = 1[/tex] (samo treba paziti da su [tex]p_1[/tex] i [tex]p_2[/tex] linearno nezavisni),
pa je jedno rjesenje: [tex](p) = \{t + 1, 2t - 1\}[/tex]
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 16:02 ned, 18. 3. 2012 Naslov: Postano: 16:02 ned, 18. 3. 2012 Naslov: |
    |
|
|
Molio bih pomoć oko dva zadatka. Unaprijed hvala.
[b][u]Prvi:[/u][/b]
Zadana je matrica
[dtex]\begin{bmatrix}
1 & 1 & 1\\
0 & -1 & 2\\
1 & 1 & 1\\
1 & 1 & 0
\end{bmatrix}[/dtex]
operatora [tex]A\colon\mathbb R^3\to M_2(\mathbb R)[/tex] u paru baza [tex]\bigg\{(1,0,1),(1,0,-1),(0,1,1)\bigg\}[/tex] i [tex]\left\{\begin{bmatrix}1&0\\ 1&1\end{bmatrix},\begin{bmatrix}1&0\\0&0\end{bmatrix},\begin{bmatrix}0&1\\0&1\end{bmatrix},\begin{bmatrix}0&0\\0&1\end{bmatrix}\right\}[/tex].
Odredite [tex]A(x_1,x_2,x_3)[/tex] za proizvoljan [tex](x_1,x_2,x_3)\in\mathbb R^3[/tex].
[b][u]Drugi:[/u][/b]
Nađite matricu operatora [tex]A\colon\mathbb R^3\to \mathcal P_2[/tex], [tex]A(x,y,z)=x+y+z+xt[/tex] u paru baza [tex]\bigg\{(1,1,0),(1,0,1),(0,0,1)\bigg\}[/tex] i [tex]\bigg\{1+t,1-2t\bigg\}[/tex].
Unaprijed puno hvala!!!
:thankyou: :thankyou: :thankyou:
Molio bih pomoć oko dva zadatka. Unaprijed hvala.
Prvi:
Zadana je matrica
[dtex]\begin{bmatrix}
1 & 1 & 1\\
0 & -1 & 2\\
1 & 1 & 1\\
1 & 1 & 0
\end{bmatrix}[/dtex]
operatora [tex]A\colon\mathbb R^3\to M_2(\mathbb R)[/tex] u paru baza [tex]\bigg\{(1,0,1),(1,0,-1),(0,1,1)\bigg\}[/tex] i [tex]\left\{\begin{bmatrix}1&0\\ 1&1\end{bmatrix},\begin{bmatrix}1&0\\0&0\end{bmatrix},\begin{bmatrix}0&1\\0&1\end{bmatrix},\begin{bmatrix}0&0\\0&1\end{bmatrix}\right\}[/tex].
Odredite [tex]A(x_1,x_2,x_3)[/tex] za proizvoljan [tex](x_1,x_2,x_3)\in\mathbb R^3[/tex].
Drugi:
Nađite matricu operatora [tex]A\colon\mathbb R^3\to \mathcal P_2[/tex], [tex]A(x,y,z)=x+y+z+xt[/tex] u paru baza [tex]\bigg\{(1,1,0),(1,0,1),(0,0,1)\bigg\}[/tex] i [tex]\bigg\{1+t,1-2t\bigg\}[/tex].
Unaprijed puno hvala!!!
  
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 18:02 ned, 18. 3. 2012 Naslov: Postano: 18:02 ned, 18. 3. 2012 Naslov: |
    |
|
|
@1. zadatak: kako bi prikazao proizvoljni [tex](x_1, x_2, x_3)[/tex] pomoću [strike]zadane[/strike] baze? :wink:
edit: zapravo, opet koristi matrice prijelaza tako da imaš matrični prikaz operatora u kanonskim bazama.
@2.zadatak: možeš "ručno" izračunati [tex]A(e_i)[/tex] u danim bazama (dakle, izračunati djelovanje operatora na elemente baze domene i onda ih prikazati pomoću baze kodomene) i složiti ih u matricu ili koristiti matrice prijelaza pa operirati s kanonskim bazama (tu ne moraš rješavati sustave, ali moraš množiti matrice i sl. pa biraj :twisted: )
@1. zadatak: kako bi prikazao proizvoljni [tex](x_1, x_2, x_3)[/tex] pomoću zadane baze? 
edit: zapravo, opet koristi matrice prijelaza tako da imaš matrični prikaz operatora u kanonskim bazama.
@2.zadatak: možeš "ručno" izračunati [tex]A(e_i)[/tex] u danim bazama (dakle, izračunati djelovanje operatora na elemente baze domene i onda ih prikazati pomoću baze kodomene) i složiti ih u matricu ili koristiti matrice prijelaza pa operirati s kanonskim bazama (tu ne moraš rješavati sustave, ali moraš množiti matrice i sl. pa biraj  ) )
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 16:01 pon, 19. 3. 2012 Naslov: Postano: 16:01 pon, 19. 3. 2012 Naslov: |
    |
|
|
Dakle, ipak ću ovo malo raspisati :D
1. zadatak: svaki je linearni operator jedinstveno zadan svojim djelovanjem na bazu (jer se svaki vektor nekog v.p. može na jedinstveni način prikazati pomoću baznih vektora) pa nam je matrični prikaz dovoljan da izvedemo nekakvu općenitu formulu djelovanja operatora.
Uvijek je zgodnije operirati s kanonskim bazama, a jedan od razloga zašto vidjet ćemo kasnije u zadatku.
Dakle, sad matricu iz jednog para baza želimo prebaciti u drugi par baza (teorem 1.4.15).
Neka su (e) i (f) kanonske, a (e') i (f') zadane baze.
Onda je naša tražena matrica:
[tex]A_{f,e}=T_{f}*A_{f',e'}*S_{e}^{-1}[/tex]
Gdje su [tex]T_{f}[/tex] i [tex]S_{e}[/tex] matrice prijelaza.
[tex]\begin{bmatrix}
&0.5 &2.5 &0.5 \\
& 1 & 1 &0\\
& 1 &1 &0\\
& 2& 1 &0
\end{bmatrix}[/tex]
Oke, što sada? Pa kako možemo prikazati proizvoljni [tex](x_1,x_2,x_3)[/tex] pomoću (kanonske) baze?
[tex](x_1,x_2,x_3)=a*e_1 + b*e_2 + c*e_3[/tex]
Mi tražimo djelovanje op. [tex]A[/tex] pa ćemo napasti taj izraz njime:
[tex]A(x_1,x_2,x_3)=A(a*e_1 + b*e_2 + c*e_3)=a*Ae_1 + b*Ae_2 + c*Ae_3[/tex]
gdje smo iskoristili aditivnost i homogenost operatora. Mi [tex]A(e_i)[/tex] znamo, pa to nam točno piše u stupcima matričnog prikaza operatora.
[tex]A(x_1,x_2,x_3)=a*(0.5,1,1,2)+b*(2.5,1,1,1)+c*(0.5,0,0,0)[/tex]
[tex]A(x_1,x_2,x_3)=(-0.5a+2.5b+0.5c,a+b,a+b,2a+b)[/tex]
Sad postaje jasno zašto smo koristili kanonsku bazu; jer su koeficijenti uz i-ti bazni vektor u prikazu proizvoljnog vektora baš i-ta komponenta tog proizvoljnog vektora; i možemo pisati
[tex]A(x_1,x_2,x_3)=(0.5x_1+2.5x_2+0.5x_3,x_1+x_2,x_1+x_2,2x_1+x_2)[/tex]
I koristeći izomorfnost [tex]M_2[/tex] i [tex]\mathbb{R^{4}}[/tex] uređenu četvorku napišemo kao matricu i zadatak je gotov.
Dakle, ipak ću ovo malo raspisati 
1. zadatak: svaki je linearni operator jedinstveno zadan svojim djelovanjem na bazu (jer se svaki vektor nekog v.p. može na jedinstveni način prikazati pomoću baznih vektora) pa nam je matrični prikaz dovoljan da izvedemo nekakvu općenitu formulu djelovanja operatora.
Uvijek je zgodnije operirati s kanonskim bazama, a jedan od razloga zašto vidjet ćemo kasnije u zadatku.
Dakle, sad matricu iz jednog para baza želimo prebaciti u drugi par baza (teorem 1.4.15).
Neka su (e) i (f) kanonske, a (e') i (f') zadane baze.
Onda je naša tražena matrica:
[tex]A_{f,e}=T_{f}*A_{f',e'}*S_{e}^{-1}[/tex]
Gdje su [tex]T_{f}[/tex] i [tex]S_{e}[/tex] matrice prijelaza.
[tex]\begin{bmatrix}
&0.5 &2.5 &0.5 \\
& 1 & 1 &0\\
& 1 &1 &0\\
& 2& 1 &0
\end{bmatrix}[/tex]
Oke, što sada? Pa kako možemo prikazati proizvoljni [tex](x_1,x_2,x_3)[/tex] pomoću (kanonske) baze?
[tex](x_1,x_2,x_3)=a*e_1 + b*e_2 + c*e_3[/tex]
Mi tražimo djelovanje op. [tex]A[/tex] pa ćemo napasti taj izraz njime:
[tex]A(x_1,x_2,x_3)=A(a*e_1 + b*e_2 + c*e_3)=a*Ae_1 + b*Ae_2 + c*Ae_3[/tex]
gdje smo iskoristili aditivnost i homogenost operatora. Mi [tex]A(e_i)[/tex] znamo, pa to nam točno piše u stupcima matričnog prikaza operatora.
[tex]A(x_1,x_2,x_3)=a*(0.5,1,1,2)+b*(2.5,1,1,1)+c*(0.5,0,0,0)[/tex]
[tex]A(x_1,x_2,x_3)=(-0.5a+2.5b+0.5c,a+b,a+b,2a+b)[/tex]
Sad postaje jasno zašto smo koristili kanonsku bazu; jer su koeficijenti uz i-ti bazni vektor u prikazu proizvoljnog vektora baš i-ta komponenta tog proizvoljnog vektora; i možemo pisati
[tex]A(x_1,x_2,x_3)=(0.5x_1+2.5x_2+0.5x_3,x_1+x_2,x_1+x_2,2x_1+x_2)[/tex]
I koristeći izomorfnost [tex]M_2[/tex] i [tex]\mathbb{R^{4}}[/tex] uređenu četvorku napišemo kao matricu i zadatak je gotov.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 17:14 pon, 19. 3. 2012 Naslov: Postano: 17:14 pon, 19. 3. 2012 Naslov: |
    |
|
|
Kod prof. Berica (09.03.)dobili smo za zadacu (poglavlje anhilatori) jedan zadatak s polinomima.
[b]ZAD:[/b] [u]U prostoru P4 polinom stp <=3 zadan je potprostor M generiran polinomima p1=1+x, p2= x+x^2. Odredite bazu za anhilator od M.[/u]
Pitanje (1): Buduci su elementi u skupu M linerarno zavisni
( x(1+x)= x+x^2), da li je onda dimenzija tog prostora 1, ili ipak gledamo samo broj elemenata u tom skupu, pa je to 2 (ma da mi to nije logicno, jer baza mora biti linearno nezavisn)
Pitanje (2): Po definiciji prostor P4 ima dimenziju 5, u ovom
slucaju ima 4 (zbog stp <=3) ?
Pitanje (3): Ako racunam da je dimM=2, nadopunim "bazu" linearne ljuske do dimenzije citavog prostora, sto zanci jos dva elementa kanonske baze treba dodati. Prema izracunima to su p3=1, i p6=x^3 (jer p4 i p5 daju linearnu kombinaciju). Da li je ovo uredu?
Ako jeste, onda bi funkcionali trebali ispasti ovako:
f3= a-b+c
f4=d
Unaprijed zahvaljujem na odgovorima. :)
Kod prof. Berica (09.03.)dobili smo za zadacu (poglavlje anhilatori) jedan zadatak s polinomima.
ZAD: U prostoru P4 polinom stp ⇐3 zadan je potprostor M generiran polinomima p1=1+x, p2= x+x^2. Odredite bazu za anhilator od M.
Pitanje (1): Buduci su elementi u skupu M linerarno zavisni
( x(1+x)= x+x^2), da li je onda dimenzija tog prostora 1, ili ipak gledamo samo broj elemenata u tom skupu, pa je to 2 (ma da mi to nije logicno, jer baza mora biti linearno nezavisn)
Pitanje (2): Po definiciji prostor P4 ima dimenziju 5, u ovom
slucaju ima 4 (zbog stp ⇐3) ?
Pitanje (3): Ako racunam da je dimM=2, nadopunim "bazu" linearne ljuske do dimenzije citavog prostora, sto zanci jos dva elementa kanonske baze treba dodati. Prema izracunima to su p3=1, i p6=x^3 (jer p4 i p5 daju linearnu kombinaciju). Da li je ovo uredu?
Ako jeste, onda bi funkcionali trebali ispasti ovako:
f3= a-b+c
f4=d
Unaprijed zahvaljujem na odgovorima. 
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 17:32 pon, 19. 3. 2012 Naslov: Postano: 17:32 pon, 19. 3. 2012 Naslov: |
    |
|
|
1.) Otkad je x skalar iz polja pa možeš njime množiti? :shock: Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) :wink:
2.) Nekad ta 4 označuje dimenziju, katkad maksimalnu potenciju. U ovom slučaju dimP=4.
3.) Trebaju ti samo još dva vektora (dimM°=dim(n) - dim(M)), nađeš dualnu bazu i onda su ti [tex]e_3^*[/tex] i [tex]e_4^*[/tex] baza za anihilator.
Rješenje: dodaš [tex]p_3=x^3[/tex] i[tex] p_4=1[/tex]; ta su četiri vektora linearno nezavisna pa tražimo im dualnu bazu.
[tex]p(x)=\alpha(1+x)+\beta(x+x^2)+\gamma(x^3)+\delta[/tex]
Izjednačimo polinome, traži nam se samo [tex]e_3^*[/tex] i [tex]e_4^*[/tex], a to su upravo [tex]\gamma=a[/tex] i [tex]\delta=d-c+b[/tex]
1.) Otkad je x skalar iz polja pa možeš njime množiti?  Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) 
2.) Nekad ta 4 označuje dimenziju, katkad maksimalnu potenciju. U ovom slučaju dimP=4.
3.) Trebaju ti samo još dva vektora (dimM°=dim(n) - dim(M)), nađeš dualnu bazu i onda su ti [tex]e_3^*[/tex] i [tex]e_4^*[/tex] baza za anihilator.
Rješenje: dodaš [tex]p_3=x^3[/tex] i[tex] p_4=1[/tex]; ta su četiri vektora linearno nezavisna pa tražimo im dualnu bazu.
[tex]p(x)=\alpha(1+x)+\beta(x+x^2)+\gamma(x^3)+\delta[/tex]
Izjednačimo polinome, traži nam se samo [tex]e_3^*[/tex] i [tex]e_4^*[/tex], a to su upravo [tex]\gamma=a[/tex] i [tex]\delta=d-c+b[/tex]
Zadnja promjena: quark; 17:42 pon, 19. 3. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 17:41 pon, 19. 3. 2012 Naslov: Postano: 17:41 pon, 19. 3. 2012 Naslov: |
    |
|
|
[quote="quark"]1.) Otkad je x skalar iz polja pa možeš njime množiti? :shock: Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) :wink:
2.) Nekad ta 4 označuje dimenziju, katkad maksimalnu potenciju. U ovom slučaju dimP=4.
3.) Trebaju ti samo još dva vektora (dimM°=dim(n) - dim(M)), nađeš dualnu bazu i onda su ti [tex]e_3^*[/tex] i [tex]e_4^*[/tex] baza za anihilator.
Rješenje: dodaš [tex]p_3=x^3[/tex] i[tex] p_4=1[/tex]; ta su četiri vektora linearno nezavisna pa tražimo im dualnu bazu.
[tex]p(x)=\alpha(1+x)+\beta(x+x^2)+\gamma(x^3)+\delta[/tex]
Izjednačimo polinome, traži nam se samo [tex]\gamma[/tex] i \[tex]delta[/tex], a to su upravo [tex]a[/tex] i [tex]d-c+b[/tex][/quote]
(1) bas sam glupko :oops: :oops: Hajd, bolje ovdje nego na kolokviju :D
Hvala, bit ce onda dobro i rjesenje.
| quark (napisa): | 1.) Otkad je x skalar iz polja pa možeš njime množiti?  Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) Ta dva vektora u M linearno su nezavisna (pa vidiš odmah po stupnjevima) 
2.) Nekad ta 4 označuje dimenziju, katkad maksimalnu potenciju. U ovom slučaju dimP=4.
3.) Trebaju ti samo još dva vektora (dimM°=dim(n) - dim(M)), nađeš dualnu bazu i onda su ti [tex]e_3^*[/tex] i [tex]e_4^*[/tex] baza za anihilator.
Rješenje: dodaš [tex]p_3=x^3[/tex] i[tex] p_4=1[/tex]; ta su četiri vektora linearno nezavisna pa tražimo im dualnu bazu.
[tex]p(x)=\alpha(1+x)+\beta(x+x^2)+\gamma(x^3)+\delta[/tex]
Izjednačimo polinome, traži nam se samo [tex]\gamma[/tex] i \[tex]delta[/tex], a to su upravo [tex]a[/tex] i [tex]d-c+b[/tex] |
(1) bas sam glupko   Hajd, bolje ovdje nego na kolokviju Hajd, bolje ovdje nego na kolokviju 
Hvala, bit ce onda dobro i rjesenje.
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 13:05 ned, 25. 3. 2012 Naslov: Postano: 13:05 ned, 25. 3. 2012 Naslov: |
    |
|
|
[quote="gflegar"]a b) ide slicno...[/quote]
Evo, rijesio i ovaj pod b), iako se moze rijesiti "slicno" to vjerojatno nije ocekivano rjesenje...
ipak se u tom slucaju treba rijesiti sustav 16 jednadzbi sa 16 nepoznanica. Evo boljeg rjesenja:
Lako se vidi da je matricni prikaz operatora [tex]B[/tex] u kanonskoj bazi:
[dtex] [B]_e^e = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 3 & 0 \\
0 & 0 & 0 & 4 \end{bmatrix}[/dtex]
Iz ovoga se odmah vidi da je karakteristicni polinom te matrice [tex]k_{[B]_e^e}(\lambda) = (1 - \lambda)(2 - \lambda)(3 - \lambda)(4 - \lambda)[/tex]
Matricni prikazi operatora u razlicitim bazama su slicne matrice, a slicne matrice imaju jednake karakteristicne polinome.
Ali, ako izracunamo [tex]det(X - 4I)[/tex] gdje je [tex]X[/tex] matrica zadana u zadatku vidimo da je ta determinanta razlicita od [tex]0[/tex], dok je [tex]k_{[B]_e^e}(4) = 0[/tex].
Dakle, ne postoji baza u kojoj operator [tex]B[/tex] ima takav matricni prikaz.
(U moju obranu, kada je ovo pitanje bilo postavljeno jos nismo radili spektar pa nisam imao dosta znanja za b) dio zadatka :) )
| gflegar (napisa): | | a b) ide slicno... |
Evo, rijesio i ovaj pod b), iako se moze rijesiti "slicno" to vjerojatno nije ocekivano rjesenje...
ipak se u tom slucaju treba rijesiti sustav 16 jednadzbi sa 16 nepoznanica. Evo boljeg rjesenja:
Lako se vidi da je matricni prikaz operatora [tex]B[/tex] u kanonskoj bazi:
[dtex] [B]_e^e = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 3 & 0 \\
0 & 0 & 0 & 4 \end{bmatrix}[/dtex]
Iz ovoga se odmah vidi da je karakteristicni polinom te matrice [tex]k_{[B]_e^e}(\lambda) = (1 - \lambda)(2 - \lambda)(3 - \lambda)(4 - \lambda)[/tex]
Matricni prikazi operatora u razlicitim bazama su slicne matrice, a slicne matrice imaju jednake karakteristicne polinome.
Ali, ako izracunamo [tex]det(X - 4I)[/tex] gdje je [tex]X[/tex] matrica zadana u zadatku vidimo da je ta determinanta razlicita od [tex]0[/tex], dok je [tex]k_{[B]_e^e}(4) = 0[/tex].
Dakle, ne postoji baza u kojoj operator [tex]B[/tex] ima takav matricni prikaz.
(U moju obranu, kada je ovo pitanje bilo postavljeno jos nismo radili spektar pa nisam imao dosta znanja za b) dio zadatka  ) )
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
|












