| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
štrumfeta
Forumaš(ica)
Pridružen/a: 02. 11. 2011. (19:36:55)
Postovi: (36)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:03 uto, 27. 3. 2012 Naslov: Postano: 16:03 uto, 27. 3. 2012 Naslov: |
    |
|
|
Funkcija je neprekidna na R. Koristeći definiciju limesa s lijeva pokaži da je [latex]\lim_{x\to 0^-}{e^{1/x}}=0.[/latex]
[spoiler]Neka je [latex]\varepsilon > 0[/latex]. Trebam naći [latex]\delta >0[/latex] td. za svaki [latex]x\in \left\langle -\delta,0\right\rangle[/latex] vrijedi [latex]|e^{1/x}|<\varepsilon[/latex], tj. [latex]e^{1/x}<\varepsilon.[/latex]
Ako je [latex]\delta_0>0[/latex], onda se pokaže da je [latex]e^{-1/\delta_0}<\varepsilon \iff \delta_0 < \frac{1}{\ln{\frac{1}{\varepsilon}}}[/latex]
Odaberimo onda, za zadani [latex]\varepsilon >0[/latex], broj [latex]\delta[/latex] td. vrijedi [latex]\delta< 1/\ln{\frac{1}{\varepsilon}}.[/latex]
Neka je [latex]-\delta < x < 0[/latex]. Jer je [latex]e^{1/x}[/latex] strogo opadajuća, onda je [latex]e^{1/x}<e^{-1/\delta}[/latex]. Prema tome, vrijedi [latex]e^{1/x}<e^{-1/\delta}<\varepsilon[/latex] za svaki [latex]x\in \left\langle -\delta,0\right\rangle[/latex], tj. [latex]\lim_{x->0^-}{e^{1/x}}=0[/latex].[/spoiler]
Funkcija je neprekidna na R. Koristeći definiciju limesa s lijeva pokaži da je 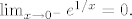
| Spoiler [hidden; click to show]: | Neka je  . Trebam naći 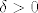 td. za svaki 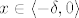 vrijedi 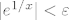 , tj. 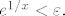
Ako je 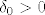 , onda se pokaže da je 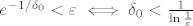
Odaberimo onda, za zadani 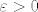 , broj  td. vrijedi 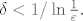
Neka je 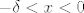 . Jer je 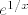 strogo opadajuća, onda je 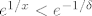 . Prema tome, vrijedi 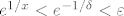 za svaki 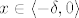 , tj. 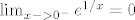 . |
_________________
The Dude Abides
|
|
| [Vrh] |
|
štrumfeta
Forumaš(ica)
Pridružen/a: 02. 11. 2011. (19:36:55)
Postovi: (36)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
štrumfeta
Forumaš(ica)
Pridružen/a: 02. 11. 2011. (19:36:55)
Postovi: (36)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 9:53 čet, 5. 4. 2012 Naslov: Postano: 9:53 čet, 5. 4. 2012 Naslov: |
    |
|
|
Molim da mi kažete gdje griješim:
Neka je [tex]y(x)=\cos (3\arcsin x)[/tex]. Odredite [tex]f^{(n)}(0)[/tex].
Dobijem diferencijalnu jednadžbu [dtex](1-x^2)y''(x)-xy'(x)+9y(x)=0.[/dtex] Deriviram tu jednakost [tex]n-2[/tex] puta i dobijem [dtex]\sum_{k=0}^{n-2}{n-2\choose k}(1-x^2)^{(k)}y^{(n-k)}-\sum_{k=0}^{n-2}{n-2\choose k}x^{(k)}y^{(n-1-k)}+9y^{(n-2)}=0[/dtex]
[dtex](1-x^2)y^{(n)}+(n-2)(-2x)y^{(n-1)}-(n-2)(n-3)y^{(n-2)}-xy^{(n-1)}-(n-2)y^{(n-2)}+9y^{(n-2)}=0[/dtex]
Za [tex]x=0[/tex] i sređivanjem dobijem
[dtex]y^{(n)}(0)=-(n-2)^2y^{(n-2)}(0)+9y^{(n-2)}(0)=\Big((n-2)-3\Big)\Big((n-2)+3\Big)y^{(n-2)}(0)=(n-5)(n+1)y^{(n-2)}(0)[/dtex]
i sad ne znam što dalje za [tex]n=2k, \ k\in\mathbb N[/tex], dok je za [tex]n=2k-1, \ k\in\mathbb N ,[/tex] očito [tex]y^{(n)}(0)=0[/tex] zbog [tex]\displaystyle y'(0)=-\sin (3\arcsin 0)\frac{3}{\sqrt{1-0^2}}=0[/tex].
Unaprijed hvala! :thankyou:
Molim da mi kažete gdje griješim:
Neka je [tex]y(x)=\cos (3\arcsin x)[/tex]. Odredite [tex]f^{(n)}(0)[/tex].
Dobijem diferencijalnu jednadžbu [dtex](1-x^2)y''(x)-xy'(x)+9y(x)=0.[/dtex] Deriviram tu jednakost [tex]n-2[/tex] puta i dobijem [dtex]\sum_{k=0}^{n-2}{n-2\choose k}(1-x^2)^{(k)}y^{(n-k)}-\sum_{k=0}^{n-2}{n-2\choose k}x^{(k)}y^{(n-1-k)}+9y^{(n-2)}=0[/dtex]
[dtex](1-x^2)y^{(n)}+(n-2)(-2x)y^{(n-1)}-(n-2)(n-3)y^{(n-2)}-xy^{(n-1)}-(n-2)y^{(n-2)}+9y^{(n-2)}=0[/dtex]
Za [tex]x=0[/tex] i sređivanjem dobijem
[dtex]y^{(n)}(0)=-(n-2)^2y^{(n-2)}(0)+9y^{(n-2)}(0)=\Big((n-2)-3\Big)\Big((n-2)+3\Big)y^{(n-2)}(0)=(n-5)(n+1)y^{(n-2)}(0)[/dtex]
i sad ne znam što dalje za [tex]n=2k, \ k\in\mathbb N[/tex], dok je za [tex]n=2k-1, \ k\in\mathbb N ,[/tex] očito [tex]y^{(n)}(0)=0[/tex] zbog [tex]\displaystyle y'(0)=-\sin (3\arcsin 0)\frac{3}{\sqrt{1-0^2}}=0[/tex].
Unaprijed hvala! 
Zadnja promjena: Zenon; 14:03 čet, 5. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 20:54 čet, 5. 4. 2012 Naslov: Postano: 20:54 čet, 5. 4. 2012 Naslov: |
    |
|
|
[quote="anamarie"]dobro ti je
za n=2k samo uvrštavaš pa dobiješ
[tex]y^{(2k)}(0)=(2k-5)(2k+1)(2k-7)(2k-1)*....*(-1)*5*(-3)*3*y^{(0)}(0)=(2k-5)!!(2k+1)!![/tex][/quote]
Ček, ček.
Faktorijele smo definirali kao [tex]n!:=n(n-1)(n-2)\cdots 3\cdot 2\cdot 1[/tex], dvofaktorijele kao [tex]n!!:=n(n-2)(n-4)\cdots 4\cdot 2[/tex] ili [tex]n!!:=n(n-2)(n-4)\cdots 3\cdot 1[/tex], ovisno o parnosti broja n, dok kod tebe [tex](2k-5)!!=(2k-5)(2k-7)\cdots 3\cdot 1\cdot (-1)\cdot (-3)[/tex].
Mislim da je onda pravilnije zapisati rješenje kao [tex](2k-5)!!(2k+1)!!\cdot (-1)\cdot (-3)=3\cdot (2k-5)!!(2k+1)!![/tex], a i treba provjeriti je li dobro sve skup, jer očito prkljamo :P
EDIT: Dobro je, i meni ispada da se ide do točno tih brojeva.
EDIT 2:
Da sada ne triple-postam :P
Molio bih provjeru n-te derivacije area sinus hiperbolnog :P
Dobio sam [dtex]f^{(n)}(0)=\begin{cases}
0 & ; & n=2k, \ k\in\mathbb N\\
(-1)^{k-2}\Big[(2k-3)!!\Big]^2 & ; & n=2k-1, \ k\in\mathbb N
\end{cases}[/dtex]
| anamarie (napisa): | dobro ti je
za n=2k samo uvrštavaš pa dobiješ
[tex]y^{(2k)}(0)=(2k-5)(2k+1)(2k-7)(2k-1)*....*(-1)*5*(-3)*3*y^{(0)}(0)=(2k-5)!!(2k+1)!![/tex] |
Ček, ček.
Faktorijele smo definirali kao [tex]n!:=n(n-1)(n-2)\cdots 3\cdot 2\cdot 1[/tex], dvofaktorijele kao [tex]n!!:=n(n-2)(n-4)\cdots 4\cdot 2[/tex] ili [tex]n!!:=n(n-2)(n-4)\cdots 3\cdot 1[/tex], ovisno o parnosti broja n, dok kod tebe [tex](2k-5)!!=(2k-5)(2k-7)\cdots 3\cdot 1\cdot (-1)\cdot (-3)[/tex].
Mislim da je onda pravilnije zapisati rješenje kao [tex](2k-5)!!(2k+1)!!\cdot (-1)\cdot (-3)=3\cdot (2k-5)!!(2k+1)!![/tex], a i treba provjeriti je li dobro sve skup, jer očito prkljamo 
EDIT: Dobro je, i meni ispada da se ide do točno tih brojeva.
EDIT 2:
Da sada ne triple-postam 
Molio bih provjeru n-te derivacije area sinus hiperbolnog 
Dobio sam [dtex]f^{(n)}(0)=\begin{cases}
0 & ; & n=2k, \ k\in\mathbb N\\
(-1)^{k-2}\Big[(2k-3)!!\Big]^2 & ; & n=2k-1, \ k\in\mathbb N
\end{cases}[/dtex]
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 12:10 sub, 7. 4. 2012 Naslov: Postano: 12:10 sub, 7. 4. 2012 Naslov: |
    |
|
|
[quote="Zenon"]A ništa, triple-post mi očito ne gine :P
OK.
Nađite sve pravce koji prolaze kroz ishodište i sijeku hiperbolu [tex]xy=a^2[/tex] pod pravim kutem.
Označimo točku presjeka s [tex]T=(x_0,y_0)[/tex].
[tex]\displaystyle xy=a^2\quad \Big/\frac{d\!x}{d\!y}[/tex]
[tex]\displaystyle y+xy'=0\Longrightarrow y'=-\frac yx[/tex], pa je onda koeficijent smjera tangente na hiperbolu u točki presjeka [tex]\displaystyle -\frac{y_0}{x_0}[/tex].
Pravac okomit na tu tangentu mora imati koeficijent smjera oblika [tex]\displaystyle\frac{x_0}{y_0}[/tex].
[dtex]y-0=\frac{x_0}{y_0}(x-0)[/dtex]
[dtex]y=\frac{x_0}{y_0}x[/dtex]
Molio bih provjeru svoga riješenja. Unaprijed hvala![/quote]
Pa trebao bi ispasti samo pravac y=x. To se lijepo moze vidjeti i sa slike.
Naime nakon sto ste zakljucili da je koeficijent smjera [tex]\frac{x_0}{y_0}[/tex], krivo ste napisali jednadzbu tangente. Treba biti:
[tex]y-y_0=\frac{x_0}{y_0}(x-x_0)[/tex].
Sada se iskoristi uvjet da pravac prolazi kroz ishodiste tako da se uvrsti x=0, y=0 te se dobije
[tex]-y_0=\frac{x_0}{y_0}(-x_0)[/tex]
Jos iskoristite da tocka [tex](x_0,y_0)[/tex] lezi na hiperboli pa je
[tex]x_0 y_0 = a^2[/tex].
| Zenon (napisa): | A ništa, triple-post mi očito ne gine 
OK.
Nađite sve pravce koji prolaze kroz ishodište i sijeku hiperbolu [tex]xy=a^2[/tex] pod pravim kutem.
Označimo točku presjeka s [tex]T=(x_0,y_0)[/tex].
[tex]\displaystyle xy=a^2\quad \Big/\frac{d\!x}{d\!y}[/tex]
[tex]\displaystyle y+xy'=0\Longrightarrow y'=-\frac yx[/tex], pa je onda koeficijent smjera tangente na hiperbolu u točki presjeka [tex]\displaystyle -\frac{y_0}{x_0}[/tex].
Pravac okomit na tu tangentu mora imati koeficijent smjera oblika [tex]\displaystyle\frac{x_0}{y_0}[/tex].
[dtex]y-0=\frac{x_0}{y_0}(x-0)[/dtex]
[dtex]y=\frac{x_0}{y_0}x[/dtex]
Molio bih provjeru svoga riješenja. Unaprijed hvala! |
Pa trebao bi ispasti samo pravac y=x. To se lijepo moze vidjeti i sa slike.
Naime nakon sto ste zakljucili da je koeficijent smjera [tex]\frac{x_0}{y_0}[/tex], krivo ste napisali jednadzbu tangente. Treba biti:
[tex]y-y_0=\frac{x_0}{y_0}(x-x_0)[/tex].
Sada se iskoristi uvjet da pravac prolazi kroz ishodiste tako da se uvrsti x=0, y=0 te se dobije
[tex]-y_0=\frac{x_0}{y_0}(-x_0)[/tex]
Jos iskoristite da tocka [tex](x_0,y_0)[/tex] lezi na hiperboli pa je
[tex]x_0 y_0 = a^2[/tex].
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
Popara
Forumaš(ica)


Pridružen/a: 17. 08. 2012. (19:05:50)
Postovi: (3B)16
Spol: 
Lokacija: Zadar/Zagreb
|
 Postano: 18:14 pet, 2. 11. 2012 Naslov: Postano: 18:14 pet, 2. 11. 2012 Naslov: |
    |
|
|
Imam jedno rješenje za provjeru:
Zadatak glasi:
Neka je [tex]f: \mathbb{R}\rightarrow \mathbb{R} [/tex] funkcija takva da za sve podskupove [tex]A,B \subseteq \mathbb{R}[/tex] vrijedi
[tex]f(A\cap B) = f(A) \cap f(B)[/tex]
Je li f injekcija?
E sad,ja tvrdim da je. To znači da moram dokazati da
[tex]f(A\cap B) = f(A) \cap f(B) \Rightarrow f[/tex] je injekcija.
Pretpostavimo suprotno,tj ovo lijevo vrijedi a f nije injekcija.
To sad znači da [tex]\exists x_{1},x_{2}\in \mathbb{R},\ x_{1}\ne x_{2} \wedge f(x_{1}) = f(x_{2})[/tex]
Uzmimo sad [tex]A=\{x_{1}\},\ B=\{x_{2}\}[/tex] a neka je [tex]f(x_{1}) = f(x_{2})=c,\ c\in \mathbb{R}[/tex]
Sada imamo [tex]A\cap B=\emptyset, f(A\cap B)=\emptyset[/tex] a [tex]f(A) \cap f(B)=\{c\}[/tex]
Što je kontradikcija sa početnom pretpostavkom da [tex]f(A\cap B) = f(A) \cap f(B)[/tex],ergo f mora biti injekcija.
Jeli to okej?
Imam jedno rješenje za provjeru:
Zadatak glasi:
Neka je [tex]f: \mathbb{R}\rightarrow \mathbb{R} [/tex] funkcija takva da za sve podskupove [tex]A,B \subseteq \mathbb{R}[/tex] vrijedi
[tex]f(A\cap B) = f(A) \cap f(B)[/tex]
Je li f injekcija?
E sad,ja tvrdim da je. To znači da moram dokazati da
[tex]f(A\cap B) = f(A) \cap f(B) \Rightarrow f[/tex] je injekcija.
Pretpostavimo suprotno,tj ovo lijevo vrijedi a f nije injekcija.
To sad znači da [tex]\exists x_{1},x_{2}\in \mathbb{R},\ x_{1}\ne x_{2} \wedge f(x_{1}) = f(x_{2})[/tex]
Uzmimo sad [tex]A=\{x_{1}\},\ B=\{x_{2}\}[/tex] a neka je [tex]f(x_{1}) = f(x_{2})=c,\ c\in \mathbb{R}[/tex]
Sada imamo [tex]A\cap B=\emptyset, f(A\cap B)=\emptyset[/tex] a [tex]f(A) \cap f(B)=\{c\}[/tex]
Što je kontradikcija sa početnom pretpostavkom da [tex]f(A\cap B) = f(A) \cap f(B)[/tex],ergo f mora biti injekcija.
Jeli to okej?
|
|
| [Vrh] |
|
grizly
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (21:30:01)
Postovi: (27)16
Spol: 
|
|
| [Vrh] |
|
linus
Forumaš(ica)


Pridružen/a: 20. 11. 2011. (16:59:13)
Postovi: (46)16
Lokacija: subnet mask
|
 Postano: 14:01 sub, 3. 11. 2012 Naslov: Postano: 14:01 sub, 3. 11. 2012 Naslov: |
    |
|
|
Trazim skup [tex]S[/tex] t.d fja [tex]f_{<-1,1/2>}: <-1,\frac{1}{2}> -> S[/tex] surjekcija, odnosno, koliko sam ja shvatio, trazim sliku intervala [tex] <-1,\frac{1}{2}>[/tex] pri funkciji [tex]f[/tex]
[dtex]f(x)=(g o h o l)(x),
l(x)=arccosx,
h(x)=\frac{x}{pi},
g(x)=log_3(x)[/dtex]
Stvar je u tome sta je u Zenonovim rjesenjima on u [tex]log_3(x)[/tex]'ubacio' [tex]<\frac{1}{3},1>[/tex], a ja sam dobio [tex]<0,\frac{1}{3}>[/tex] sto saljem u [tex]log_3(x)[/tex] i onda dobijem [tex]<-\infty, -1>[/tex] sto je ocito razlicito, ali ne vidim gresku jer je redom
[dtex]l(<-1,\frac{1}{2}>)=arccos(<-1,\frac{1}{2}>)=<0,\frac{\pi}{3}>[/dtex]
[dtex]h(<0,\frac{\pi}{3}>)=\frac{x}{\pi}(<0,\frac{\pi}{3}>)=<0,\frac{1}{3}>[/dtex]
[dtex]g(<0,\frac{1}{3}>)=log_3(<0,\frac{1}{3}>)=<-\infty,-1>[/dtex]
Ne kazem da je Zenon pogrijesio samo da mi ukazete ako netko vidi gdje je greska jer ja ne shvacam, hvala unaprijed
Trazim skup [tex]S[/tex] t.d fja [tex]f_{←1,1/2>}: ←1,\frac{1}{2}> → S[/tex] surjekcija, odnosno, koliko sam ja shvatio, trazim sliku intervala [tex] ←1,\frac{1}{2}>[/tex] pri funkciji [tex]f[/tex]
[dtex]f(x)=(g o h o l)(x),
l(x)=arccosx,
h(x)=\frac{x}{pi},
g(x)=log_3(x)[/dtex]
Stvar je u tome sta je u Zenonovim rjesenjima on u [tex]log_3(x)[/tex]'ubacio' [tex]<\frac{1}{3},1>[/tex], a ja sam dobio [tex]<0,\frac{1}{3}>[/tex] sto saljem u [tex]log_3(x)[/tex] i onda dobijem [tex]←\infty, -1>[/tex] sto je ocito razlicito, ali ne vidim gresku jer je redom
[dtex]l(←1,\frac{1}{2}>)=arccos(←1,\frac{1}{2}>)=<0,\frac{\pi}{3}>[/dtex]
[dtex]h(<0,\frac{\pi}{3}>)=\frac{x}{\pi}(<0,\frac{\pi}{3}>)=<0,\frac{1}{3}>[/dtex]
[dtex]g(<0,\frac{1}{3}>)=log_3(<0,\frac{1}{3}>)=←\infty,-1>[/dtex]
Ne kazem da je Zenon pogrijesio samo da mi ukazete ako netko vidi gdje je greska jer ja ne shvacam, hvala unaprijed
|
|
| [Vrh] |
|
|










