| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 17:14 pon, 9. 4. 2012 Naslov: Postano: 17:14 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]
da, na demonstraturama je rijesen tako da smo trazili n-tu derivaciju i koristili se tom trecom formulom. ((h)^n+1)/n+1 *M
Da li mozemo rijesiti pomocu formule za 1/8 * delta ^2 * M2(f) ?[/quote]
Onda mi se čini da je demos pogriješio. Ta druga formula mi se čini dobra.
A što se tiče tog 2. zadatka iz 2011., prilično sam zbunjen. Općenito postoje dvije različite stvari:
1.) greška odbacivanja;
2.) greška zbog računanja u aritmetici konačne preciznosti.
Prva se računa se kao što je to maločas učinio Phoenix, ili pomoću Taylorovog teorema srednje vrijednosti. Vezana je za egzaktnu aritmetiku, a ne za aritmetiku računala (primijetite da Phoenix nije nigdje koristio svojstva aritmetike računala).
U drugoj valja promatrati predznake pribrojnika, kao i omjer najvećeg pribrojnika i traženog rezultata, da bismo ga usporedili sa strojnom točnošću, float ili double. [b]EDIT:[/b] bio sam malo zabrijao, ovdje ne treba promatrati omjer jer su pribrojnici istog predznaka. Ako se u zadatku traži samo ovo drugo (kao što Phoenix kaže u donjem postu), ispada trivijalan. [b]EDIT 2:[/b] kao što je ispod napisao Dofalol, u drugoj grupi nije tako. Ispada da je zadatak ili trivijalan ili nerješiv.
| Anonymous (napisa): |
da, na demonstraturama je rijesen tako da smo trazili n-tu derivaciju i koristili se tom trecom formulom. ((h)^n+1)/n+1 *M
Da li mozemo rijesiti pomocu formule za 1/8 * delta ^2 * M2(f) ? |
Onda mi se čini da je demos pogriješio. Ta druga formula mi se čini dobra.
A što se tiče tog 2. zadatka iz 2011., prilično sam zbunjen. Općenito postoje dvije različite stvari:
1.) greška odbacivanja;
2.) greška zbog računanja u aritmetici konačne preciznosti.
Prva se računa se kao što je to maločas učinio Phoenix, ili pomoću Taylorovog teorema srednje vrijednosti. Vezana je za egzaktnu aritmetiku, a ne za aritmetiku računala (primijetite da Phoenix nije nigdje koristio svojstva aritmetike računala).
U drugoj valja promatrati predznake pribrojnika, kao i omjer najvećeg pribrojnika i traženog rezultata, da bismo ga usporedili sa strojnom točnošću, float ili double. EDIT: bio sam malo zabrijao, ovdje ne treba promatrati omjer jer su pribrojnici istog predznaka. Ako se u zadatku traži samo ovo drugo (kao što Phoenix kaže u donjem postu), ispada trivijalan. EDIT 2: kao što je ispod napisao Dofalol, u drugoj grupi nije tako. Ispada da je zadatak ili trivijalan ili nerješiv.
Zadnja promjena: satja; 18:06 pon, 9. 4. 2012; ukupno mijenjano 4 put/a.
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 18:13 pon, 9. 4. 2012 Naslov: Postano: 18:13 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Dofalol"]Pogledaj si drugu grupu, taj već je teži.
Imaš članove koji stalno mijenjaju predznak pa bi trebalo komentirati odnos najvećeg člana po apsolutnoj vrijednosti i traženog rješenja, a ne vidim neki pametan način da izračunamo to traženo rješenje...[/quote]
Pa jedna ideja za a) dio tog zadatka, mislim na [latex]\displaystyle\sum_{k = 0}^{\infty} \frac{(- \frac{1}{2}x^2)^k}{k!(2k+3)!!}[/latex]
Znači, kad je x = -0.5, imamo
[latex]\displaystyle\sum_{k = 0}^{\infty} \frac{(-1)^k}{16^k k! (2k+3)!!} <\displaystyle\sum_{k = 0}^{\infty} \frac{1}{16^k k! (2k+3)!!} < \displaystyle\sum_{k = 0}^{\infty} \frac{1}{16^k} = 1.06667 [/latex]
Slična se ocjena može dati i odozdola, pa se vidi da je suma koju trebamo izračunati negdje jaaako blizu jedinici.
I još sam prilično grubo ovo ocjenjivao...
| Dofalol (napisa): | Pogledaj si drugu grupu, taj već je teži.
Imaš članove koji stalno mijenjaju predznak pa bi trebalo komentirati odnos najvećeg člana po apsolutnoj vrijednosti i traženog rješenja, a ne vidim neki pametan način da izračunamo to traženo rješenje... |
Pa jedna ideja za a) dio tog zadatka, mislim na 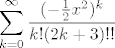
Znači, kad je x = -0.5, imamo
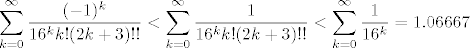
Slična se ocjena može dati i odozdola, pa se vidi da je suma koju trebamo izračunati negdje jaaako blizu jedinici.
I još sam prilično grubo ovo ocjenjivao...
Zadnja promjena: ceps; 18:20 pon, 9. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
minnie m.
Forumaš(ica)

Pridružen/a: 06. 10. 2011. (20:34:28)
Postovi: (16)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 21:04 pon, 9. 4. 2012 Naslov: Postano: 21:04 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Phoenix"]Nakon proučavanja jednih jako zanimljivih dodatnih materijala čini mi se da je rješenje tog zadatka zapravo vrlo jednostavno: rezultat u računalu nastaje zbrajanjem pozitivnih sumanada pa neće doći do katastrofalnog kraćenja, stoga se suma reda točno izračuna, a zatim isto tako i produkt iste suma i broja ispred nje. Ukratko.
Toliko o komplikacijama i teškom zadatku s kolokvija. :)[/quote]
ali bi jos uvijek trebalo provjerit ako je ostatak reda neki relativno malen broj, pa mislim da je ok (i nuzno) ono tvoje
vidim da u ovim materijalima s fsb-a ne komentiraju to, ali moze se dogodit da neki clan sume bude manji od epsilon, ali da onda neki/svi clanovi nakon njega divljaju. svejedno tesko sumnjam da bi dali takvu funkciju, ni da ce pazit na ovakvo nesto
| Phoenix (napisa): | Nakon proučavanja jednih jako zanimljivih dodatnih materijala čini mi se da je rješenje tog zadatka zapravo vrlo jednostavno: rezultat u računalu nastaje zbrajanjem pozitivnih sumanada pa neće doći do katastrofalnog kraćenja, stoga se suma reda točno izračuna, a zatim isto tako i produkt iste suma i broja ispred nje. Ukratko.
Toliko o komplikacijama i teškom zadatku s kolokvija.  |
ali bi jos uvijek trebalo provjerit ako je ostatak reda neki relativno malen broj, pa mislim da je ok (i nuzno) ono tvoje
vidim da u ovim materijalima s fsb-a ne komentiraju to, ali moze se dogodit da neki clan sume bude manji od epsilon, ali da onda neki/svi clanovi nakon njega divljaju. svejedno tesko sumnjam da bi dali takvu funkciju, ni da ce pazit na ovakvo nesto
|
|
| [Vrh] |
|
Dama Herc
Forumaš(ica)

Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Dama Herc
Forumaš(ica)

Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Kirgudu
Forumaš(ica)

Pridružen/a: 23. 01. 2011. (17:55:43)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
 Postano: 18:57 sub, 26. 5. 2012 Naslov: Postano: 18:57 sub, 26. 5. 2012 Naslov: |
    |
|
|
Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5.
Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 19:10 sub, 26. 5. 2012 Naslov: Postano: 19:10 sub, 26. 5. 2012 Naslov: |
    |
|
|
[quote="pupi"]Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5.[/quote]
demos je rekao da je zadnji,tj u ovom slučaju x^3, tj da je 3 stupanj egzaktnosti.
možda je pogrješio?
| pupi (napisa): | Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5. |
demos je rekao da je zadnji,tj u ovom slučaju x^3, tj da je 3 stupanj egzaktnosti.
možda je pogrješio?
|
|
| [Vrh] |
|
Gost
|
 Postano: 19:51 sub, 26. 5. 2012 Naslov: Postano: 19:51 sub, 26. 5. 2012 Naslov: |
    |
|
|
[quote="pupi"]Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5.[/quote]
znaci ak imam npr. 3 nepoznanice racunam do x^2? neovisno o tom kolka je greska, tj. dal je razlicita od 0?
| pupi (napisa): | Imas četiri nepoznanice : w1,w2,w3, x2, pa uvrstavavas za f 1,x,x^2,x^3 uz uvjet da je greska jednaka 0 (trebaju ti 4 jednadzbe).
Polinomni stupanj egzaknosti je ja mislim barem 2n-1 , dakle ta integracijska formula je tocna za polinome stupnja manjeg ili jednakog 5. |
znaci ak imam npr. 3 nepoznanice racunam do x^2? neovisno o tom kolka je greska, tj. dal je razlicita od 0?
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
 Postano: 19:55 sub, 26. 5. 2012 Naslov: Postano: 19:55 sub, 26. 5. 2012 Naslov: |
    |
|
|
Hm , vjerojatnije sam ja nes krivo shvatila nego je demos falija :D
Ja sam to gore zakljucila po Teoremu 1 na stranici 40 u materijalima: I. Beroš: Uvod u numeričku matematiku: vježbe, 2002/2003. (do nelinearnih jednadžbi, nekorigirana verzija).
@gost:Da, ako imas tri nepoznanice onda uvrstavas 1,x,x^2 i zahtjevas da greska bude 0 :)
Hm , vjerojatnije sam ja nes krivo shvatila nego je demos falija 
Ja sam to gore zakljucila po Teoremu 1 na stranici 40 u materijalima: I. Beroš: Uvod u numeričku matematiku: vježbe, 2002/2003. (do nelinearnih jednadžbi, nekorigirana verzija).
@gost:Da, ako imas tri nepoznanice onda uvrstavas 1,x,x^2 i zahtjevas da greska bude 0 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|












