| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
mono
Forumaš(ica)
Pridružen/a: 16. 09. 2011. (13:04:01)
Postovi: (E)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 18:31 pon, 16. 4. 2012 Naslov: Postano: 18:31 pon, 16. 4. 2012 Naslov: |
    |
|
|
Promatram [latex]\theta[/latex] na onaj način da smije ići od 0 do [latex]\pi[/latex]:
[latex]\varphi \in [0, 2 \pi][/latex]
[latex]\theta \in [0, \frac{\pi}{6}][/latex]
Za fiksirani [latex]\theta[/latex] [latex]r \in [\frac{\sqrt{3}}{cos \theta}, 2][/latex]
Bar je meni tako ispalo. :D
Nisi pitao za objašnjenje, pa se neću bezveze mučiti ovo pokušavati objasniti bez crtanja, samo tekstom... Ali ako te ipak zanima, mogu pokušati.
Promatram 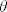 na onaj način da smije ići od 0 do na onaj način da smije ići od 0 do  : :
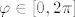
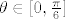
Za fiksirani 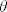 
Bar je meni tako ispalo. 
Nisi pitao za objašnjenje, pa se neću bezveze mučiti ovo pokušavati objasniti bez crtanja, samo tekstom... Ali ako te ipak zanima, mogu pokušati.
|
|
| [Vrh] |
|
mono
Forumaš(ica)
Pridružen/a: 16. 09. 2011. (13:04:01)
Postovi: (E)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
 Postano: 10:27 uto, 17. 4. 2012 Naslov: Postano: 10:27 uto, 17. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"]Promatram [latex]\theta[/latex] na onaj način da smije ići od 0 do [latex]\pi[/latex]:
[latex]\varphi \in [0, 2 \pi][/latex]
[latex]\theta \in [0, \frac{\pi}{6}][/latex]
Za fiksirani [latex]\theta[/latex] [latex]r \in [\frac{\sqrt{3}}{cos \theta}, 2][/latex]
Bar je meni tako ispalo. :D
Nisi pitao za objašnjenje, pa se neću bezveze mučiti ovo pokušavati objasniti bez crtanja, samo tekstom... Ali ako te ipak zanima, mogu pokušati.[/quote]
bi li mogao ovo malo objasnit? :)
| ceps (napisa): | Promatram 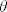 na onaj način da smije ići od 0 do na onaj način da smije ići od 0 do  : :
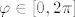
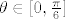
Za fiksirani 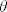 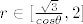
Bar je meni tako ispalo. 
Nisi pitao za objašnjenje, pa se neću bezveze mučiti ovo pokušavati objasniti bez crtanja, samo tekstom... Ali ako te ipak zanima, mogu pokušati. |
bi li mogao ovo malo objasnit? 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 11:06 uto, 17. 4. 2012 Naslov: Postano: 11:06 uto, 17. 4. 2012 Naslov: |
    |
|
|
@pupi
http://degiorgi.math.hr/forum/viewtopic.php?t=17915
Tu se već dosta pričalo o tom zadatku.
@jabuka
Da, treba ispasti kao odsječen gornji dio kugle.
[latex]\varphi[/latex] ti je jasan, pa krećem od [latex]\theta[/latex]:
Uvrsti [latex]z = \sqrt{3}[/latex] u jednadžbu sfere i dobit ćeš da je presjek sfere i te ravnine kružnica radijusa 1 sa centrom u [latex](0, 0,\sqrt{3})[/latex]
Nacrtaj si presjek ovog područja i xz-ravnine (ili yz-ravnine, svejedno, isto će ispasti (zašto?) ) kao što je to radio asistent Gogić na vježbama.
Trebalo bi ti ispasti nešto ovako:
http://www.wolframalpha.com/input/?i=x%5E2+%2B+z%5E2+%3C+4%2C+z+%3E+sqrt%283%29
Kad gledaš ovu sliku (probaj si zamisliti da su i nacrtane koordinatne osi :D ), [latex]\theta[/latex] je odmak od z-osi.
Vidimo da ide od 0 do kuta koji sa z-osi zatvara pravac koji spaja ishodište i rub ovog lika.
Zvuči malo nespretno ovako, ali ako si nacrtaš mislim da će ti biti jasno.
Koji je to kut?
Promatraj pravokutni trokut koji spaja ishodište, [latex](0, 0, \sqrt{3})[/latex] i rub ovog lika.
Tom trokutu znamo dvije stranice: [latex]\sqrt{3}[/latex] (z-os) i 1 (radijus kružnice o kojoj sam pričao na početku)
Trigonometrijom se iz ovog dobije da je [latex]\theta = \frac{\pi}{6}[/latex]
Jel sve jasno zasad? :D
Gledajmo ovu sličicu sa Wolfram Alphe. Primijeti da donji rub ovog lika dolazi od ravnine, a gornji od sfere.
Za fiksirani [latex]\theta[/latex], r ide od nekog [latex]x[/latex] do 2.
2 je tu zbog sfere, a taj nepoznati [latex]x[/latex] je tu zbog ravnine. Ostaje odgovoriti što je to [latex]x[/latex].
Sad malo crtanja - fiksiraj neki [latex]\theta[/latex] i povuci pravac koji ide iz ishodišta, a odmaknut je od z-osi upravo za [latex]\theta[/latex]. Gledaj pravokutni trokut ishodište - [latex](0, 0, \sqrt{3})[/latex] - točka gdje taj pravac sječe ravninu z = \sqrt{3}.
Iz tog pravokutnog trokuta imaš [latex]\sqrt{3} = rcos \theta[/latex].
Nespretno je ovo objašnjavati bez olovke, papira i skiciranja, ali nadam se da sam bar nešto pojasnio. Viči ako ti neki korak nije jasan.
@pupi
http://degiorgi.math.hr/forum/viewtopic.php?t=17915
Tu se već dosta pričalo o tom zadatku.
@jabuka
Da, treba ispasti kao odsječen gornji dio kugle.
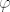 ti je jasan, pa krećem od ti je jasan, pa krećem od 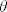 : :
Uvrsti 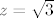 u jednadžbu sfere i dobit ćeš da je presjek sfere i te ravnine kružnica radijusa 1 sa centrom u u jednadžbu sfere i dobit ćeš da je presjek sfere i te ravnine kružnica radijusa 1 sa centrom u 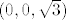
Nacrtaj si presjek ovog područja i xz-ravnine (ili yz-ravnine, svejedno, isto će ispasti (zašto?) ) kao što je to radio asistent Gogić na vježbama.
Trebalo bi ti ispasti nešto ovako:
http://www.wolframalpha.com/input/?i=x%5E2+%2B+z%5E2+%3C+4%2C+z+%3E+sqrt%283%29
Kad gledaš ovu sliku (probaj si zamisliti da su i nacrtane koordinatne osi  ), ), 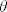 je odmak od z-osi. je odmak od z-osi.
Vidimo da ide od 0 do kuta koji sa z-osi zatvara pravac koji spaja ishodište i rub ovog lika.
Zvuči malo nespretno ovako, ali ako si nacrtaš mislim da će ti biti jasno.
Koji je to kut?
Promatraj pravokutni trokut koji spaja ishodište, 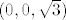 i rub ovog lika. i rub ovog lika.
Tom trokutu znamo dvije stranice: 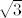 (z-os) i 1 (radijus kružnice o kojoj sam pričao na početku) (z-os) i 1 (radijus kružnice o kojoj sam pričao na početku)
Trigonometrijom se iz ovog dobije da je 
Jel sve jasno zasad? 
Gledajmo ovu sličicu sa Wolfram Alphe. Primijeti da donji rub ovog lika dolazi od ravnine, a gornji od sfere.
Za fiksirani 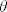 , r ide od nekog , r ide od nekog  do 2. do 2.
2 je tu zbog sfere, a taj nepoznati  je tu zbog ravnine. Ostaje odgovoriti što je to je tu zbog ravnine. Ostaje odgovoriti što je to  . .
Sad malo crtanja - fiksiraj neki 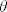 i povuci pravac koji ide iz ishodišta, a odmaknut je od z-osi upravo za i povuci pravac koji ide iz ishodišta, a odmaknut je od z-osi upravo za 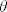 . Gledaj pravokutni trokut ishodište - . Gledaj pravokutni trokut ishodište - 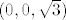 - točka gdje taj pravac sječe ravninu z = \sqrt{3}. - točka gdje taj pravac sječe ravninu z = \sqrt{3}.
Iz tog pravokutnog trokuta imaš 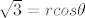 . .
Nespretno je ovo objašnjavati bez olovke, papira i skiciranja, ali nadam se da sam bar nešto pojasnio. Viči ako ti neki korak nije jasan.
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
 Postano: 13:12 uto, 17. 4. 2012 Naslov: Postano: 13:12 uto, 17. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"]@pupi
http://degiorgi.math.hr/forum/viewtopic.php?t=17915
Tu se već dosta pričalo o tom zadatku.[/quote]Oki, kako su razlicite godine nisam primjetila da se radi o istom tipu zadatka :D
Tnx
EDIT: Ako neko rijesi taj zadatak do kraja (2011,drugi) jel moze napisat rezultat , jer meni ispada 0 , a to mi je malo sumnjivo , hh . :D
[size=9][color=#999999]Added after 40 minutes:[/color][/size]
EDIT1: Jel mozemo u tom drugom iz 2010. racunat integral od sqrt3 do 2 od (4-z^2)*pi po z , kao kad smo racunali one V1 i V2 da bi izracunali neki volumen? (Provjerila sam i moze , racun je dosta jednostavniji, ako koga veseli.)
Oki, kako su razlicite godine nisam primjetila da se radi o istom tipu zadatka 
Tnx
EDIT: Ako neko rijesi taj zadatak do kraja (2011,drugi) jel moze napisat rezultat , jer meni ispada 0 , a to mi je malo sumnjivo , hh . 
Added after 40 minutes:
EDIT1: Jel mozemo u tom drugom iz 2010. racunat integral od sqrt3 do 2 od (4-z^2)*pi po z , kao kad smo racunali one V1 i V2 da bi izracunali neki volumen? (Provjerila sam i moze , racun je dosta jednostavniji, ako koga veseli.)
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
penkala
Forumaš(ica)

Pridružen/a: 17. 04. 2012. (14:25:45)
Postovi: (4)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
|









