U ovom primjeru se "ide obratno". Ne konstruiraš iz φ, N i H semidirektan produkt G, nego već imaš zadanu grupu i podgrupe i tražiš automorfizam iz kojega G nastaje.
U ovom konkretnom slučaju pošto je [latex]H = \mathbb Z/2\mathbb Z \cong \langle b\rangle[/latex], φ je vrlo jednostavna: [latex]\phi_e = 1_N, \phi_b(a) = bab^{-1}[/latex] = (u diedralnoj grupi) = [latex]a^{-1}[/latex] tj. φ_b je invertiranje (za što bismo mogli reći da je urpavo drugi istaknuti automorfizam Abelove grupe).
Općenito, semidirektan produkt grupa je grupa s nekim produktom, i na njega ne moraš gledati kao da je definiran s φ nego da jednostavno je ono što je (npr. kompozicija simetrija n-terokuta), i onda se pitati kako φ rekonstruirati. Tvrdnja iz skripte je da to možemo učiniti (nakon što odredimo N i H td. je N normalna, NH = G i NnH = {e}) promatrajući unutrašnje automorfizme I_h, za h u H.
U ovom primjeru se "ide obratno". Ne konstruiraš iz φ, N i H semidirektan produkt G, nego već imaš zadanu grupu i podgrupe i tražiš automorfizam iz kojega G nastaje.
U ovom konkretnom slučaju pošto je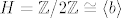 
, φ je vrlo jednostavna: 
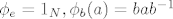= (u diedralnoj grupi) = 
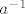tj. φ_b je invertiranje (za što bismo mogli reći da je urpavo drugi istaknuti automorfizam Abelove grupe).
Općenito, semidirektan produkt grupa je grupa s nekim produktom, i na njega ne moraš gledati kao da je definiran s φ nego da jednostavno je ono što je (npr. kompozicija simetrija n-terokuta), i onda se pitati kako φ rekonstruirati. Tvrdnja iz skripte je da to možemo učiniti (nakon što odredimo N i H td. je N normalna, NH = G i NnH = {e}) promatrajući unutrašnje automorfizme I_h, za h u H.
_________________
The lyf so short, the craft so long to lerne
