Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Integral?
WWW:
Idite na Prethodno  1, 2, 3, 4, 5, 6, 7  Sljedeće
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
quark
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: muško
Sarma = la pohva - posuda
20 = 26 - 6
PostPostano: 19:28 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
[quote="Shaman"]
ovaj sa sinusima i kosinusima nisam skroz siguran, prvo podijelis s cos^4(x), u nazivniku imas tg^4(x)+1 i stavis t=tg(x) dt=1/cos^2(x)dx pa ti u brojniku ostane 1/cos^2(x)=1+tg^(x).
Ono sto nisam siguran da vrijedi 4*integral od 0 do pi/2 = pocetnom integralu, onda bi integral kojeg dobijes bio 4*lim(integral(od 0 do B) od (1+t^2)/(t^4+1)) kada B ide u beskonacno.
nazivnik napises (t^2+1)^2-2*t^2 to sada napises kao razliku kvadrata i rastavis na parcijalne razlomke.
nakon toga nekakvim dodavanjima/oduzimanjima i nadopunjavanjem do potpunog kvadrata mozes to rijesiti.[/quote]

Kako si se ti riješio tu kosinusa? Ako izlučiš u nazivniku, supstitucijom riješiš se samo [tex]\cos^2(x)[/tex], ostane ti još toliko?
Shaman (napisa):

ovaj sa sinusima i kosinusima nisam skroz siguran, prvo podijelis s cos^4(x), u nazivniku imas tg^4(x)+1 i stavis t=tg(x) dt=1/cos^2(x)dx pa ti u brojniku ostane 1/cos^2(x)=1+tg^(x).
Ono sto nisam siguran da vrijedi 4*integral od 0 do pi/2 = pocetnom integralu, onda bi integral kojeg dobijes bio 4*lim(integral(od 0 do B) od (1+t^2)/(t^4+1)) kada B ide u beskonacno.
nazivnik napises (t^2+1)^2-2*t^2 to sada napises kao razliku kvadrata i rastavis na parcijalne razlomke.
nakon toga nekakvim dodavanjima/oduzimanjima i nadopunjavanjem do potpunog kvadrata mozes to rijesiti.


Kako si se ti riješio tu kosinusa? Ako izlučiš u nazivniku, supstitucijom riješiš se samo [tex]\cos^2(x)[/tex], ostane ti još toliko?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Shaman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: muško
Sarma = la pohva - posuda
5 = 9 - 4
PostPostano: 19:29 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
1/cos^2(x)=1+tg^2(x)
1/cos^2(x)=1+tg^2(x)



_________________
it was merely a setback
[Vrh]
Korisnički profil Pošaljite privatnu poruku
quark
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: muško
Sarma = la pohva - posuda
20 = 26 - 6
PostPostano: 19:34 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
[quote="Shaman"]1/cos^2(x)=1+tg^2(x)[/quote]

Moje isprike, zanemarih da je recipročno :oops:
Shaman (napisa):
1/cos^2(x)=1+tg^2(x)


Moje isprike, zanemarih da je recipročno Embarassed


[Vrh]
Korisnički profil Pošaljite privatnu poruku
malalodacha
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
Sarma = la pohva - posuda
-24 = 9 - 33
PostPostano: 21:33 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
može netko riješit suma od 1 do beskonačno (4n+3) / 5^n ? traži se konačna suma tog reda
može netko riješit suma od 1 do beskonačno (4n+3) / 5^n ? traži se konačna suma tog reda


[Vrh]
Korisnički profil Pošaljite privatnu poruku
quark
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: muško
Sarma = la pohva - posuda
20 = 26 - 6
PostPostano: 22:21 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
[quote="malalodacha"]može netko riješit suma od 1 do beskonačno (4n+3) / 5^n ? traži se konačna suma tog reda[/quote]

Za početak, po D'Alembertovu kriteriju suma konvergira.
Sad želiš iskoristiti Taylorove redove i svesti sume na funkcije.
U ovom slučaju, trebaš iskoristiti sumu geometrijskog reda; rastavimo na dvije sume:

[latex]4\cdot\sum_{n=1}^{\infty}\frac{ n}{5^n}+3\cdot\sum_{n=1}^{\infty}(\frac{1}{5})^n[/latex]

Samo, geometrijski red ide od 0 (to lagano riješiš manipulacijom n-a), ali veći problem, ova prva suma ne odgovara pa moraš izvesti formulu za:

[latex]\sum_{n=1}^{\infty}n\cdot x^n[/latex], naravno [tex]x=\frac{1}{3}[/tex].

To pokušaj sama derivirajući gornji izraz i onda množeći x-om :wink:

[spoiler]Ako se ne varam, ispada 2.[/spoiler]
malalodacha (napisa):
može netko riješit suma od 1 do beskonačno (4n+3) / 5^n ? traži se konačna suma tog reda


Za početak, po D'Alembertovu kriteriju suma konvergira.
Sad želiš iskoristiti Taylorove redove i svesti sume na funkcije.
U ovom slučaju, trebaš iskoristiti sumu geometrijskog reda; rastavimo na dvije sume:



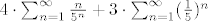
Samo, geometrijski red ide od 0 (to lagano riješiš manipulacijom n-a), ali veći problem, ova prva suma ne odgovara pa moraš izvesti formulu za:

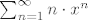, naravno [tex]x=\frac{1}{3}[/tex].

To pokušaj sama derivirajući gornji izraz i onda množeći x-om Wink

Spoiler [hidden; click to show]:


[Vrh]
Korisnički profil Pošaljite privatnu poruku
malalodacha
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
Sarma = la pohva - posuda
-24 = 9 - 33
PostPostano: 22:47 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
dobro sam mislio dakle, i x je 1/5 :)

[size=9][color=#999999]Added after 3 minutes:[/color][/size]

http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1112-int.pdf može 4. zadatak iz dijela na ploči, onaj sa xcosx -sinx u brojniku? treba mi neki hint za početak, a wolfram neće
dobro sam mislio dakle, i x je 1/5 Smile

Added after 3 minutes:

http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1112-int.pdf može 4. zadatak iz dijela na ploči, onaj sa xcosx -sinx u brojniku? treba mi neki hint za početak, a wolfram neće


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Shaman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: muško
Sarma = la pohva - posuda
5 = 9 - 4
PostPostano: 23:19 uto, 22. 5. 2012    Naslov: Citirajte i odgovorite
[quote="malalodacha"]dobro sam mislio dakle, i x je 1/5 :)

[size=9][color=#999999]Added after 3 minutes:[/color][/size]

http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1112-int.pdf može 4. zadatak iz dijela na ploči, onaj sa xcosx -sinx u brojniku? treba mi neki hint za početak, a wolfram neće[/quote]

u brojniku dodaj x i -x pa rastavi na 2 integrala(I=I(1)+I(2))
I(1)= integral od 1/(x-sin(x))
I(2)=integral od (x*cos(x)-x)/(x-sin(x))^2, izluci x u brojniku i parcijalno integriraj u=x v=integral od od ostatka kojeg mozes lagano supstitucijom rijesiti, dobije se da je I(2)=x/(x-sinx)+I(1) sto uvristi u I=I(1)-I(2) i konacno rjesenje je x/(x-sinx) +c

[size=9][color=#999999]Added after 1 minutes:[/color][/size]

I(2)=-x/(x-sinx)+I(1) *
malalodacha (napisa):
dobro sam mislio dakle, i x je 1/5 Smile

Added after 3 minutes:

http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1112-int.pdf može 4. zadatak iz dijela na ploči, onaj sa xcosx -sinx u brojniku? treba mi neki hint za početak, a wolfram neće


u brojniku dodaj x i -x pa rastavi na 2 integrala(I=I(1)+I(2))
I(1)= integral od 1/(x-sin(x))
I(2)=integral od (x*cos(x)-x)/(x-sin(x))^2, izluci x u brojniku i parcijalno integriraj u=x v=integral od od ostatka kojeg mozes lagano supstitucijom rijesiti, dobije se da je I(2)=x/(x-sinx)+I(1) sto uvristi u I=I(1)-I(2) i konacno rjesenje je x/(x-sinx) +c

Added after 1 minutes:

I(2)=-x/(x-sinx)+I(1) *



_________________
it was merely a setback
[Vrh]
Korisnički profil Pošaljite privatnu poruku
dalmatinčica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
Sarma = la pohva - posuda
6 = 10 - 4
PostPostano: 18:43 sri, 23. 5. 2012    Naslov: Citirajte i odgovorite
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf
može li netko pomoći oko 2. a) 2. ili 4. grupa

hvala
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf
može li netko pomoći oko 2. a) 2. ili 4. grupa

hvala


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Shaman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: muško
Sarma = la pohva - posuda
5 = 9 - 4
PostPostano: 20:51 sri, 23. 5. 2012    Naslov: Citirajte i odgovorite
1. arcsin(x)= pi/2-arccos(x), t=arccos(x)
2. -t+pi/2=z

1. raspises kotangens, t=sin(x)
2. v=(1-t^3)^(1/2), dobije se -2/3* integral od dv/(1-v^2)
3. parcijalni razlomci

rijesavas po definiciji nepravog integrala, samo pazi na granice
1. arcsin(x)= pi/2-arccos(x), t=arccos(x)
2. -t+pi/2=z

1. raspises kotangens, t=sin(x)
2. v=(1-t^3)^(1/2), dobije se -2/3* integral od dv/(1-v^2)
3. parcijalni razlomci

rijesavas po definiciji nepravog integrala, samo pazi na granice



_________________
it was merely a setback
[Vrh]
Korisnički profil Pošaljite privatnu poruku
dalmatinčica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
Sarma = la pohva - posuda
6 = 10 - 4
PostPostano: 21:15 sri, 23. 5. 2012    Naslov: Citirajte i odgovorite
a dio sa isitajte konvergenciju?
je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?
a dio sa isitajte konvergenciju?
je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
5_ra
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 12. 2011. (15:37:14)
Postovi: (28)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 11:53 pet, 25. 5. 2012    Naslov: Citirajte i odgovorite
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko rec kako bi isao 2.a u c grupi?
hvala unaprijed
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko rec kako bi isao 2.a u c grupi?
hvala unaprijed


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Zenon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
PostPostano: 22:58 pet, 1. 6. 2012    Naslov: Citirajte i odgovorite
Molio bih pomoć oko ispitivanja konvergencije nepravog integrala. Čak mislim da sam ga jednom i rješio, ali sada sam totalno isključen :S
[dtex]\int_e ^{+\infty}\frac{d\!x}{\sqrt{1+x}\ln x}[/dtex]
Unaprijed hvala! :thankyou:
Molio bih pomoć oko ispitivanja konvergencije nepravog integrala. Čak mislim da sam ga jednom i rješio, ali sada sam totalno isključen :S
[dtex]\int_e ^{+\infty}\frac{d\!x}{\sqrt{1+x}\ln x}[/dtex]
Unaprijed hvala! Thank you



_________________
It's a wonderful, wonderful life!
[tex]\heartsuit \ \mathcal{PMF-MO} \ \heartsuit[/tex]
[tex]\mathbb Z\Sigma\mathbb N\emptyset\mathbb N[/tex]
[Vrh]
Korisnički profil Pošaljite privatnu poruku
malalodacha
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
Sarma = la pohva - posuda
-24 = 9 - 33
PostPostano: 2:08 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0506-kol2.pdf može 4.a) iz grupa C i D?
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0506-kol2.pdf može 4.a) iz grupa C i D?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
student_92
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
Sarma = la pohva - posuda
10 = 16 - 6
PostPostano: 11:16 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="dalmatinčica"]je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?[/quote]

I mene to zanima. Ako netko zna, bilo bi lijepo od njega da odgovori. Dakle zadatak 2.a) iz druge grupe sa http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf
dalmatinčica (napisa):
je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?


I mene to zanima. Ako netko zna, bilo bi lijepo od njega da odgovori. Dakle zadatak 2.a) iz druge grupe sa http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf


[Vrh]
Korisnički profil Pošaljite privatnu poruku
anamarie
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: žensko
Sarma = la pohva - posuda
5 = 13 - 8
PostPostano: 11:45 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="student_92"][quote="dalmatinčica"]je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?[/quote]

I mene to zanima. Ako netko zna, bilo bi lijepo od njega da odgovori. Dakle zadatak 2.a) iz druge grupe sa http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf[/quote]
dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..
prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je

[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx
student_92 (napisa):
dalmatinčica (napisa):
je li tu dovoljno izračunati nepravi integral, pa ako je konačan reći da stoga konvergira ili moram to posebno pokazati?
ako da, kako?


I mene to zanima. Ako netko zna, bilo bi lijepo od njega da odgovori. Dakle zadatak 2.a) iz druge grupe sa http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..
prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je

[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx


[Vrh]
Korisnički profil Pošaljite privatnu poruku
student_92
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
Sarma = la pohva - posuda
10 = 16 - 6
PostPostano: 12:22 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="anamarie"]dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je
[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx[/quote]

Ja sam u međuvremenu dobio ovakav odgovor, [i]citiram[/i]:
[tex]\frac{arccos(x)}{\sqrt{(1-x^2)arcsin(x)}} \leq \frac{arccos(x)}{\sqrt{(1-x^2)x}} \leq \frac{\pi}{\sqrt{x-x^3}} \leq \frac{\pi}{\sqrt{x}}[/tex]
Prva nejednakost je iz činjenice da je [tex]sin(x) \leq x[/tex] za [tex]x[/tex]-eve nešto veće od [tex]0[/tex]. Druga je zbog slike funkcije [tex]arccos[/tex].

Uglavnom, s obzirom na tekst zadatka čini mi se da najprije treba provesti diskusiju o konvergenciji pa tek onda računati (ako konvergira). Neka me netko ispravi ako krivo mislim.
anamarie (napisa):
dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je
[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx


Ja sam u međuvremenu dobio ovakav odgovor, citiram:
[tex]\frac{arccos(x)}{\sqrt{(1-x^2)arcsin(x)}} \leq \frac{arccos(x)}{\sqrt{(1-x^2)x}} \leq \frac{\pi}{\sqrt{x-x^3}} \leq \frac{\pi}{\sqrt{x}}[/tex]
Prva nejednakost je iz činjenice da je [tex]sin(x) \leq x[/tex] za [tex]x[/tex]-eve nešto veće od [tex]0[/tex]. Druga je zbog slike funkcije [tex]arccos[/tex].

Uglavnom, s obzirom na tekst zadatka čini mi se da najprije treba provesti diskusiju o konvergenciji pa tek onda računati (ako konvergira). Neka me netko ispravi ako krivo mislim.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Vishykc
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: muško
Sarma = la pohva - posuda
5 = 17 - 12
Lokacija: Zagreb
PostPostano: 14:35 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
Molim pomoć oko 2.45 b) Ne čini se težak, ali..
http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_5.pdf
Molim pomoć oko 2.45 b) Ne čini se težak, ali..
http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_5.pdf



_________________
U matematici se sve smije, osim pogriješiti!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
PermutiranoPrase
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
10 = 17 - 7
PostPostano: 14:58 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
Rastaviš [tex]tgx = \frac{\sin x}{\cos x} = \sin x \cos ^{-1} x[/tex], pa uzmeš dalje radiš po smjernicama za rješavanje integrala od [tex]\sin^n x \cos ^m x[/tex]. :)
Rastaviš [tex]tgx = \frac{\sin x}{\cos x} = \sin x \cos ^{-1} x[/tex], pa uzmeš dalje radiš po smjernicama za rješavanje integrala od [tex]\sin^n x \cos ^m x[/tex]. Smile



_________________
With great power comes great electricity bill.
n!!!!
Theorem 2: Alexander the Great did not exist and he had an infinite number of limbs.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Shaman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: muško
Sarma = la pohva - posuda
5 = 9 - 4
PostPostano: 16:33 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="Vishykc"]Molim pomoć oko 2.45 b) Ne čini se težak, ali..
http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_5.pdf[/quote]

kad imas tg na neku potenciju dobra metoda je staviti t=tg(x), iz toga slijedi da je arctg(t)=x a a dx=dt/(1+t^2), pa u konkretnom zadatku imas t^5/(1+t^2) pa sad to podijelis i nesto dobis onda...
Vishykc (napisa):
Molim pomoć oko 2.45 b) Ne čini se težak, ali..
http://web.math.pmf.unizg.hr/nastava/analiza/files/ch2_5.pdf


kad imas tg na neku potenciju dobra metoda je staviti t=tg(x), iz toga slijedi da je arctg(t)=x a a dx=dt/(1+t^2), pa u konkretnom zadatku imas t^5/(1+t^2) pa sad to podijelis i nesto dobis onda...



_________________
it was merely a setback
[Vrh]
Korisnički profil Pošaljite privatnu poruku
anamarie
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: žensko
Sarma = la pohva - posuda
5 = 13 - 8
PostPostano: 17:18 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="student_92"][quote="anamarie"]dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je
[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx[/quote]

Ja sam u međuvremenu dobio ovakav odgovor, [i]citiram[/i]:
[tex]\frac{arccos(x)}{\sqrt{(1-x^2)arcsin(x)}} \leq \frac{arccos(x)}{\sqrt{(1-x^2)x}} \leq \frac{\pi}{\sqrt{x-x^3}} \leq \frac{\pi}{\sqrt{x}}[/tex]
Prva nejednakost je iz činjenice da je [tex]sin(x) \leq x[/tex] za [tex]x[/tex]-eve nešto veće od [tex]0[/tex]. Druga je zbog slike funkcije [tex]arccos[/tex].

Uglavnom, s obzirom na tekst zadatka čini mi se da najprije treba provesti diskusiju o konvergenciji pa tek onda računati (ako konvergira). Neka me netko ispravi ako krivo mislim.[/quote]
u pravu si,ovdje je baš naglašeno da treba ispitati konvergenciju prije računanja,ali ako nije naglašeno onda je dovoljno izračunati
student_92 (napisa):
anamarie (napisa):
dovoljno je izračunati nepravi integral jer već time dobiješ da li kovergira ili ne..prvo idi parcijalnom integracijom,staviš u=arccosx,a
[tex] dv=\frac{2}{2\sqrt{(1-x^2)arcsinx}} [/tex] pa je
[tex] v=2\sqrt{arcsinx} [/tex]
pa kasnije supstucijom t=arcsinx


Ja sam u međuvremenu dobio ovakav odgovor, citiram:
[tex]\frac{arccos(x)}{\sqrt{(1-x^2)arcsin(x)}} \leq \frac{arccos(x)}{\sqrt{(1-x^2)x}} \leq \frac{\pi}{\sqrt{x-x^3}} \leq \frac{\pi}{\sqrt{x}}[/tex]
Prva nejednakost je iz činjenice da je [tex]sin(x) \leq x[/tex] za [tex]x[/tex]-eve nešto veće od [tex]0[/tex]. Druga je zbog slike funkcije [tex]arccos[/tex].

Uglavnom, s obzirom na tekst zadatka čini mi se da najprije treba provesti diskusiju o konvergenciji pa tek onda računati (ako konvergira). Neka me netko ispravi ako krivo mislim.

u pravu si,ovdje je baš naglašeno da treba ispitati konvergenciju prije računanja,ali ako nije naglašeno onda je dovoljno izračunati


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2, 3, 4, 5, 6, 7  Sljedeće
Stranica 3 / 7.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan