| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
 Postano: 16:41 ned, 3. 6. 2012 Naslov: Postano: 16:41 ned, 3. 6. 2012 Naslov: |
    |
|
|
[quote="simon11"][quote="malalodacha"](x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?[/quote]
[latex]\frac{x^4}{(16+x^4)^2}=\frac{1}{16+x^4}-\frac{16}{(16+x^4)^2}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16(1+\frac{x^4}{16})}[/latex]
[latex]t=-\frac{x^4}{16}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16}\sum_{n=0}^{\infty}(-\frac{x^4}{16})^n=\sum_{n=0}^{\infty}\frac{(-1)^n}{16^{n+1}}x^{4n}[/latex]
sada deriviraj s lijeve strane se dobije
[latex]\frac{-4x^3}{(16+x^4)^2}[/latex] pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican :)
[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:
2. [size=18][tex]\sum\frac{n!}{n^n}[/tex][/size][/quote]
ako se izracuna
[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]
dakle nije zadovoljen nuzan uvjet [latex]\rightarrow [\latex] divergira
[quote]1.[latex]\sum\frac{cos(\frac{n\pi}{2})}{\sqrt{n}}[/latex]
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
[latex]\frac{(-1)^n}{\sqrt(n)}[/latex] sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje[/quote]
za ovaj 1. zadatak, mogu li ja razviti u red [latex]\frac{1}{(16+x^4)^2}[/latex] i onda samo to pomnožiti s x^4 ?
| simon11 (napisa): | | malalodacha (napisa): | | (x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno? |
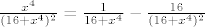
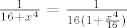
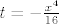
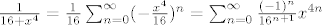
sada deriviraj s lijeve strane se dobije
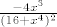 pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican 
| piccola (napisa): | Može pomoć? Treba ispitati konvergenciju redova:
2. [tex]\sum\frac{n!}{n^n}[/tex] |
ako se izracuna
[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]
dakle nije zadovoljen nuzan uvjet 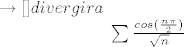
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
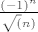 sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje |
za ovaj 1. zadatak, mogu li ja razviti u red 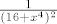 i onda samo to pomnožiti s x^4 ? i onda samo to pomnožiti s x^4 ?
Zadnja promjena: dalmatinčica; 16:43 ned, 3. 6. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
 Postano: 16:43 ned, 3. 6. 2012 Naslov: Postano: 16:43 ned, 3. 6. 2012 Naslov: |
    |
|
|
[quote="simon11"][quote="malalodacha"](x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?[/quote]
[latex]\frac{x^4}{(16+x^4)^2}=\frac{1}{16+x^4}-\frac{16}{(16+x^4)^2}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16(1+\frac{x^4}{16})}[/latex]
[latex]t=-\frac{x^4}{16}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16}\sum_{n=0}^{\infty}(-\frac{x^4}{16})^n=\sum_{n=0}^{\infty}\frac{(-1)^n}{16^{n+1}}x^{4n}[/latex]
sada deriviraj s lijeve strane se dobije
[latex]\frac{-4x^3}{(16+x^4)^2}[/latex] pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican :)
[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:
2. [size=18][tex]\sum\frac{n!}{n^n}[/tex][/size][/quote]
ako se izracuna
[latex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\latex]
dakle nije zadovoljen nuzan uvjet [latex]\rightarrow [\latex] divergira
[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:
1. [size=18][latex]\sum\frac{cos(\frac{n\pi}{2})}{\sqrt{n}[/latex][/size][/quote]
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
[latex]\frac{(-1)^n}{\sqrt(n)}[/latex] sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje[/quote]
| simon11 (napisa): | | malalodacha (napisa): | | (x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno? |
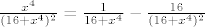
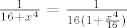
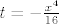
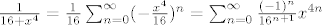
sada deriviraj s lijeve strane se dobije
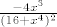 pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican 
| piccola (napisa): | Može pomoć? Treba ispitati konvergenciju redova:
2. [tex]\sum\frac{n!}{n^n}[/tex] |
ako se izracuna
 [/size] [/size] |
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
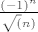 sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje[/quote] sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje[/quote]
_________________ 
getting recognized |
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
 Postano: 16:45 ned, 3. 6. 2012 Naslov: Postano: 16:45 ned, 3. 6. 2012 Naslov: |
    |
|
|
Može pomoć sa 3b) iz prve grupe?
Može pomoć sa 3b) iz prve grupe?
| Description: |
|

Download |
| Filename: |
ma2-0910-kol2.pdf |
| Filesize: |
34.93 KB |
| Downloaded: |
174 Time(s) |
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
 Postano: 17:05 ned, 3. 6. 2012 Naslov: Postano: 17:05 ned, 3. 6. 2012 Naslov: |
    |
|
|
[quote="dalmatinčica"][quote="simon11"][quote="malalodacha"](x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?[/quote]
[latex]\frac{x^4}{(16+x^4)^2}=\frac{1}{16+x^4}-\frac{16}{(16+x^4)^2}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16(1+\frac{x^4}{16})}[/latex]
[latex]t=-\frac{x^4}{16}[/latex]
[latex]\frac{1}{16+x^4}=\frac{1}{16}\sum_{n=0}^{\infty}(-\frac{x^4}{16})^n=\sum_{n=0}^{\infty}\frac{(-1)^n}{16^{n+1}}x^{4n}[/latex]
sada deriviraj s lijeve strane se dobije
[latex]\frac{-4x^3}{(16+x^4)^2}[/latex] pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican :)
[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:
2. [size=18][tex]\sum\frac{n!}{n^n}[/tex][/size][/quote]
ako se izracuna
[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]
dakle nije zadovoljen nuzan uvjet [latex]\rightarrow [\latex] divergira
[quote]1.[latex]\sum\frac{cos(\frac{n\pi}{2})}{\sqrt{n}}[/latex]
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
[latex]\frac{(-1)^n}{\sqrt(n)}[/latex] sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje[/quote]
za ovaj 1. zadatak, mogu li ja razviti u red [latex]\frac{1}{(16+x^4)^2}[/latex] i onda samo to pomnožiti s x^4 ?[/quote]
| dalmatinčica (napisa): | | simon11 (napisa): | | malalodacha (napisa): | | (x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno? |
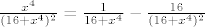
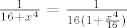
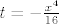
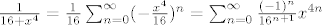
sada deriviraj s lijeve strane se dobije
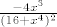 pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican 
| piccola (napisa): | Može pomoć? Treba ispitati konvergenciju redova:
2. [tex]\sum\frac{n!}{n^n}[/tex] |
ako se izracuna
[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]
dakle nije zadovoljen nuzan uvjet 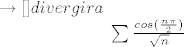
nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr
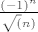 sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje |
za ovaj 1. zadatak, mogu li ja razviti u red 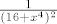 i onda samo to pomnožiti s x^4 ? i onda samo to pomnožiti s x^4 ? |
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 18:22 ned, 3. 6. 2012 Naslov: Postano: 18:22 ned, 3. 6. 2012 Naslov: |
    |
|
|
[quote="dalmatinčica"][quote="gflegar"][quote="dalmatinčica"][quote="gflegar"][quote="student_92"]Ajd netko da mi samo da ideju kako odrediti funkciju koja ima Taylorov red (oko 0) [b][tex]f(x)=\sum_{n=0}^\infty (\frac{1+n^2}{2^n})x^n[/tex][/b]?[/quote]
[dtex] f(x)=\sum_{n=0}^\infty \frac{1+n^2}{2^n}x^n = \sum_{n=0}^\infty \frac{n(n-1) + n + 1}{2^n}x^n = x^2 \sum_{n=2}^\infty \frac{n(n-1)}{2^n}x^{n-2} + x \sum_{n=1}^\infty \frac{n}{2^n}x^{n - 1} + \sum_{n=0}^\infty \frac{1}{2^n}x^n [/dtex]
Dovoljna ideja? :)[/quote]
opet, jel možemo tu sumu razdvojit i promatrat
sumu (x/2)^n
i
sumu n^2 * (x/2)^n
i samo to pozbrojit?[/quote]
pa mozes, ali neznam cemu te to vodi... kako mislis izracunati [tex]\displaystyle \sum_{n=0}^\infty \frac{n^2}{2^n}x^n[/tex]?[/quote]
na vježbama smo izvodili formulu za taj red s n^2
(derivirali, množili s x, i još jednom tako 1/(1-x) = suma x^n )
jel mogu to koristit?[/quote]
ako ti je tako draze, mozes... mada mislim da je to kompliciranije.
| dalmatinčica (napisa): | | gflegar (napisa): | | dalmatinčica (napisa): | | gflegar (napisa): | | student_92 (napisa): | | Ajd netko da mi samo da ideju kako odrediti funkciju koja ima Taylorov red (oko 0) [tex]f(x)=\sum_{n=0}^\infty (\frac{1+n^2}{2^n})x^n[/tex]? |
[dtex] f(x)=\sum_{n=0}^\infty \frac{1+n^2}{2^n}x^n = \sum_{n=0}^\infty \frac{n(n-1) + n + 1}{2^n}x^n = x^2 \sum_{n=2}^\infty \frac{n(n-1)}{2^n}x^{n-2} + x \sum_{n=1}^\infty \frac{n}{2^n}x^{n - 1} + \sum_{n=0}^\infty \frac{1}{2^n}x^n [/dtex]
Dovoljna ideja?  |
opet, jel možemo tu sumu razdvojit i promatrat
sumu (x/2)^n
i
sumu n^2 * (x/2)^n
i samo to pozbrojit? |
pa mozes, ali neznam cemu te to vodi... kako mislis izracunati [tex]\displaystyle \sum_{n=0}^\infty \frac{n^2}{2^n}x^n[/tex]? |
na vježbama smo izvodili formulu za taj red s n^2
(derivirali, množili s x, i još jednom tako 1/(1-x) = suma x^n )
jel mogu to koristit? |
ako ti je tako draze, mozes... mada mislim da je to kompliciranije.
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
aj_ca_volin_te
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
|
|
| [Vrh] |
|
|











