| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
 Postano: 16:41 pet, 27. 4. 2012 Naslov: Postano: 16:41 pet, 27. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]Zadatak sa kolokvija.
Neka je B={f:Z -> <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva[/quote]
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa.
| Anonymous (napisa): | Zadatak sa kolokvija.
Neka je B={f:Z → <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva |
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa.
|
|
| [Vrh] |
|
Gost
|
 Postano: 17:21 pet, 27. 4. 2012 Naslov: Postano: 17:21 pet, 27. 4. 2012 Naslov: |
    |
|
|
[quote="kslaven"][quote="Anonymous"]Zadatak sa kolokvija.
Neka je B={f:Z -> <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva[/quote]
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa.[/quote]
Hvala na odgovoru.
Ja sam se više orijentirala na x-eve umjesto da gledam da li vrijedi za sve funkcije...
Drugi put ću (valjda) biti pametnija :)
| kslaven (napisa): | | Anonymous (napisa): | Zadatak sa kolokvija.
Neka je B={f:Z → <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva |
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa. |
Hvala na odgovoru.
Ja sam se više orijentirala na x-eve umjesto da gledam da li vrijedi za sve funkcije...
Drugi put ću (valjda) biti pametnija 
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 11:45 ned, 4. 11. 2012 Naslov: Postano: 11:45 ned, 4. 11. 2012 Naslov: |
    |
|
|
[quote="marsupial"]http://web.math.pmf.unizg.hr/nastava/alg/2011-12/AS1kol_2012.pdf
...može pomoć oko 3. i 4. zadatka? :) :roll:[/quote]
A što ti točno nije jasno? Ovo baš i nisu komplicirani zadaci, rekao bih da provjeravaju da li imaš dobro razumijevanje nekih osnovnih ideja iz ovog kolegija.
Koje te ideje točno muče? Ajde, postavit ću ti par pitanja koja će te voditi prema rješenju. :D
3. Kako izgleda [latex]\mathbb{Z}_{60}[/latex]? Što je to red podgrupe? Kako bi onda izgledala podgrupa reda 12? Općenito, kakvi elementi generiraju grupe [latex]\mathbb{Z}_n[/latex]?
4. a) OK, ovaj baš i ne provjerava osnovne ideje algebarskih, ali se isti takav radi na vježbama., tj. bar se radio u moje vrijeme. Što je red permutacije? Ja kažem da je red od (1 3 5) 3, a red od (4 7) 2. Da li shvaćaš zašto je to tako? Red njihove kompozicije je najmanji zajednički višekratnik od 2 i 3, tj. 6.
Reci ako ti treba ovo malo bolje objasniti, drage volje. Ovo se može zapravo shvatiti na prilično intuitivan način.
b) Ako razumiješ što je to red elementa i kako izgleda [latex]\mathbb{R} / \mathbb{Z}[/latex], odgovor bi ti uz malo razmišljanja trebao biti jasan (i iznenađujuće jednostavan).
Mislim da ti identificiranje onog što točno ne shvaćaš iz Algebarskih više pomaže nego da ja sad tu samo napišem rješenja, a ti se misliš vau, ja ovo ne kužim.
| marsupial (napisa): | http://web.math.pmf.unizg.hr/nastava/alg/2011-12/AS1kol_2012.pdf
...može pomoć oko 3. i 4. zadatka?   |
A što ti točno nije jasno? Ovo baš i nisu komplicirani zadaci, rekao bih da provjeravaju da li imaš dobro razumijevanje nekih osnovnih ideja iz ovog kolegija.
Koje te ideje točno muče? Ajde, postavit ću ti par pitanja koja će te voditi prema rješenju. 
3. Kako izgleda 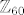 ? Što je to red podgrupe? Kako bi onda izgledala podgrupa reda 12? Općenito, kakvi elementi generiraju grupe ? Što je to red podgrupe? Kako bi onda izgledala podgrupa reda 12? Općenito, kakvi elementi generiraju grupe 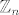 ? ?
4. a) OK, ovaj baš i ne provjerava osnovne ideje algebarskih, ali se isti takav radi na vježbama., tj. bar se radio u moje vrijeme. Što je red permutacije? Ja kažem da je red od (1 3 5) 3, a red od (4 7) 2. Da li shvaćaš zašto je to tako? Red njihove kompozicije je najmanji zajednički višekratnik od 2 i 3, tj. 6.
Reci ako ti treba ovo malo bolje objasniti, drage volje. Ovo se može zapravo shvatiti na prilično intuitivan način.
b) Ako razumiješ što je to red elementa i kako izgleda 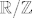 , odgovor bi ti uz malo razmišljanja trebao biti jasan (i iznenađujuće jednostavan). , odgovor bi ti uz malo razmišljanja trebao biti jasan (i iznenađujuće jednostavan).
Mislim da ti identificiranje onog što točno ne shvaćaš iz Algebarskih više pomaže nego da ja sad tu samo napišem rješenja, a ti se misliš vau, ja ovo ne kužim.
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 19:34 ned, 4. 11. 2012 Naslov: Postano: 19:34 ned, 4. 11. 2012 Naslov: |
    |
|
|
[quote="marsupial"]ako imaš drage volje vremena bilo bi mi drago da raspišeš taj 4. pod b :)
i... trebala bi mi pomoć iz 2. zadatka također!
hvala ti ;)[/quote]
Što dobijemo kad ''prerežemo'' [latex]\mathbb{R}[/latex] sa [latex]\mathbb{Z}[/latex]? Klase oblika [latex]r + \mathbb{Z}, r \in \mathbb{R} [/latex], a dva broja su u istoj klasi ako im je razlika u [latex]\mathbb{Z}[/latex] - primjeri:
[latex]\frac{5}{2}[/latex] i [latex]\frac{1}{2}[/latex] su u istoj klasi jer je [latex]\frac{5}{2} - \frac{1}{2} = 4 \in \mathbb{Z}[/latex].
[latex]4.28[/latex] i [latex]87.28[/latex] su istoj klasi iz istog razloga. Jel vidiš uzorak ovdje?
Brojevi sa istim decimalnim dijelom su u istim klasama. Što nam je u [latex]\mathbb{R} / \mathbb{Z}[/latex] nula? Klasa koja sadrži sve cijele brojeve, tj. sam [latex]\mathbb{Z}[/latex]
Što je to red elementa? Neformalno rečeno, to je broj koji nam govori koliko puta trebamo zbrojiti broj sam sa sobom da bi dobili 0.
Npr. ako zbrojimo 0.1 sa samim sobom 10 puta, dobit ćemo 1 - tj. u
[latex]\mathbb{R} / \mathbb{Z}[/latex] red od [latex]0.1 + \mathbb{Z}[/latex] je 10.
E sad, ja tvrdim da je tvoj skup A [b]upravo[/b] [latex]\mathbb{N}[/latex].
Jednu inkluziju već imaš, trebaš samo pokazati da je [latex]\mathbb{N} \subseteq A[/latex], tj za svaki [latex]n \in \mathbb{N} [/latex] moraš naći neki element iz [latex]\mathbb{R} / \mathbb{Z}[/latex] koji kad zbrojiš n puta sa samim sobom dobiješ nulu. Mislim da nije teško nakon što si vidjela ovo sa 10 i 0.1.
| marsupial (napisa): | ako imaš drage volje vremena bilo bi mi drago da raspišeš taj 4. pod b 
i... trebala bi mi pomoć iz 2. zadatka također!
hvala ti  |
Što dobijemo kad ''prerežemo''  sa sa 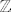 ? Klase oblika ? Klase oblika 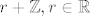 , a dva broja su u istoj klasi ako im je razlika u , a dva broja su u istoj klasi ako im je razlika u 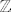 - primjeri: - primjeri:
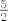 i i 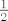 su u istoj klasi jer je su u istoj klasi jer je 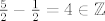 . .
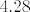 i i 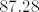 su istoj klasi iz istog razloga. Jel vidiš uzorak ovdje? su istoj klasi iz istog razloga. Jel vidiš uzorak ovdje?
Brojevi sa istim decimalnim dijelom su u istim klasama. Što nam je u 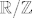 nula? Klasa koja sadrži sve cijele brojeve, tj. sam nula? Klasa koja sadrži sve cijele brojeve, tj. sam 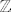
Što je to red elementa? Neformalno rečeno, to je broj koji nam govori koliko puta trebamo zbrojiti broj sam sa sobom da bi dobili 0.
Npr. ako zbrojimo 0.1 sa samim sobom 10 puta, dobit ćemo 1 - tj. u
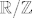 red od red od  je 10. je 10.
E sad, ja tvrdim da je tvoj skup A upravo 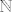 . .
Jednu inkluziju već imaš, trebaš samo pokazati da je 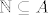 , tj za svaki , tj za svaki 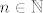 moraš naći neki element iz moraš naći neki element iz 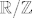 koji kad zbrojiš n puta sa samim sobom dobiješ nulu. Mislim da nije teško nakon što si vidjela ovo sa 10 i 0.1. koji kad zbrojiš n puta sa samim sobom dobiješ nulu. Mislim da nije teško nakon što si vidjela ovo sa 10 i 0.1.
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 2:08 uto, 6. 11. 2012 Naslov: Postano: 2:08 uto, 6. 11. 2012 Naslov: |
    |
|
|
[quote="Anonymous"][quote="kslaven"][quote="Anonymous"]Zadatak sa kolokvija.
Neka je B={f:Z -> <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva[/quote]
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa.[/quote]
Hvala na odgovoru.
Ja sam se više orijentirala na x-eve umjesto da gledam da li vrijedi za sve funkcije...
Drugi put ću (valjda) biti pametnija :)[/quote]
Moze li ovdje netko jos precizno napisati kako je dokazao grupoidnost i polugrupu (asocijativnost) ?
P.s. Uspjela sam :)
| Anonymous (napisa): | | kslaven (napisa): | | Anonymous (napisa): | Zadatak sa kolokvija.
Neka je B={f:Z → <0,+besk>}
Neka su f,g iz skupa B. imamo operaciju * definiranu sa f*g=mg(1)f(x).
gdje je m element iz Z.
Da li je B uz operaciju * polugrupa,monoid ili grupa?
Da li bi netko to mogao riješiti?
Za grupoidnost i asocijativnost mi je jasno da li i zašto vrijede.
Zapela sam kod neutralnog elementa.
Znači pretp. sam da postoji neutralni element e. I uzmem proizvoljni element f iz B.
f*e=e*f
me(1)f(x)=mf(1)e(x)
I što sada? Znam da ovo vrijedi za x=1...
* Z=skup cijelih brojeva |
m je bio prirodan, a ne cijeli broj. Da je m bio cijeli broj, grupoidnost ne bi morala vrijediti.
Za neutralni element mora vrijediti
me(1)f(x)=mf(1)e(x)=f(x),
za sve cijele brojeve x i za sve f-je f iz B. Iz desne jednakosti mogu izraziti f-ju e pomoću f-je f:
[tex]e=\frac{1}{mf(1)}f[/tex]
pa, ako neutralni element postoji, gornja jednakost mora vrijediti za sve f-je f iz B, što je kontradikcija. Dakle, nema neutralnog elementa. |
Hvala na odgovoru.
Ja sam se više orijentirala na x-eve umjesto da gledam da li vrijedi za sve funkcije...
Drugi put ću (valjda) biti pametnija  |
Moze li ovdje netko jos precizno napisati kako je dokazao grupoidnost i polugrupu (asocijativnost) ?
P.s. Uspjela sam 
|
|
| [Vrh] |
|
linus
Forumaš(ica)


Pridružen/a: 20. 11. 2011. (16:59:13)
Postovi: (46)16
Lokacija: subnet mask
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
_eternity
Forumaš(ica)

Pridružen/a: 08. 01. 2012. (13:53:51)
Postovi: (8)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
|












