| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gina
Gost
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 16:44 pon, 2. 8. 2004 Naslov: Postano: 16:44 pon, 2. 8. 2004 Naslov: |
    |
|
|
Skup A je konacan ako postoji prirodan broj n t.d. postoji bijekcija izmedju skupova A i {1,2,3,...,n}. (ukratko konacan skup je onaj koji ima konacno mnogo elemenata)
Skup A je prebrojiv ako postoji bijekcija izmedju A i |N (A ~ |N).
Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N.
U engleskom jeziku postoje dva termina:
[i]denurable[/i] - u bijekciji s |N
[i]countable[/i] - konacan ili u bijekciji s |N.
Je li sad jasnije?
Skup A je konacan ako postoji prirodan broj n t.d. postoji bijekcija izmedju skupova A i {1,2,3,...,n}. (ukratko konacan skup je onaj koji ima konacno mnogo elemenata)
Skup A je prebrojiv ako postoji bijekcija izmedju A i |N (A ~ |N).
Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N.
U engleskom jeziku postoje dva termina:
denurable - u bijekciji s |N
countable - konacan ili u bijekciji s |N.
Je li sad jasnije?
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 8:58 uto, 3. 8. 2004 Naslov: Postano: 8:58 uto, 3. 8. 2004 Naslov: |
    |
|
|
[quote="mdoko"]Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N.[/quote]
Mislim da vise zbunjuje sam naziv [b]prebrojiv[/b]. :? To aludira da se njegovi elementi mogu [b]prebrojati[/b]. :-s Zato je mene, dok sam bio "mali", zbunjivalo da [i]kako se mogu [b]prebrojati[/b] elementi skupa IN[/i]? :-k
Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i [b]IZ[/b]brojati (sve) njegove elemente... 8) Mozda bi "[i]brojiv[/i]" bio sretniji naziv? :lol: ;)
| mdoko (napisa): | | Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N. |
Mislim da vise zbunjuje sam naziv prebrojiv.  To aludira da se njegovi elementi mogu prebrojati. To aludira da se njegovi elementi mogu prebrojati.  Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN? Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN? 
Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i IZbrojati (sve) njegove elemente...  Mozda bi "brojiv" bio sretniji naziv? Mozda bi "brojiv" bio sretniji naziv?  
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 16:19 uto, 3. 8. 2004 Naslov: Postano: 16:19 uto, 3. 8. 2004 Naslov: |
    |
|
|
[quote="vsego"]
Mislim da vise zbunjuje sam naziv [b]prebrojiv[/b]. :? To aludira da se njegovi elementi mogu [b]prebrojati[/b]. :-s Zato je mene, dok sam bio "mali", zbunjivalo da [i]kako se mogu [b]prebrojati[/b] elementi skupa IN[/i]? :-k
[/quote]
Vidis, nisam o tome nikad razmisljao na takav nacin, mozda bi stvarno brojiv bio sretniji naziv, ali s druge strane nije li svaki skup koji se moze dobro urediti brojiv :grebgreb: :?:
| vsego (napisa): |
Mislim da vise zbunjuje sam naziv prebrojiv.  To aludira da se njegovi elementi mogu prebrojati. To aludira da se njegovi elementi mogu prebrojati.  Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN? Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN? 
|
Vidis, nisam o tome nikad razmisljao na takav nacin, mozda bi stvarno brojiv bio sretniji naziv, ali s druge strane nije li svaki skup koji se moze dobro urediti brojiv  
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 16:59 uto, 3. 8. 2004 Naslov: Postano: 16:59 uto, 3. 8. 2004 Naslov: |
    |
|
|
[quote="mdoko"][quote="vsego"]Mislim da vise zbunjuje sam naziv [b]prebrojiv[/b]. :? To aludira da se njegovi elementi mogu [b]prebrojati[/b]. :-s Zato je mene, dok sam bio "mali", zbunjivalo da [i]kako se mogu [b]prebrojati[/b] elementi skupa IN[/i]? :-k[/quote]
Vidis, nisam o tome nikad razmisljao na takav nacin, mozda bi stvarno brojiv bio sretniji naziv, ali s druge strane nije li svaki skup koji se moze dobro urediti brojiv :grebgreb: :?:[/quote]
Sure thing. 8) Ono "[i]brojiv[/i]" sam dao samo kao primjer... ;)
Mozda bi to mogli zvati "[i]prirodan skup[/i]"? :-k Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti... :| Ipak sam se probudio prije samo 20ak minuta... :shock: :oops: ;)
Besides, nece nitko poslusati nase prijedloge odavde, pa nam se bas i ne isplati trud oko trazenja pogodnijeg imena. :| Mene bi zanimalo odakle taj naziv "[i]prebrojiv[/i]" koji se ocito koristi i u drugim jezicima... :-k
| mdoko (napisa): | | vsego (napisa): | Mislim da vise zbunjuje sam naziv prebrojiv.  To aludira da se njegovi elementi mogu prebrojati. To aludira da se njegovi elementi mogu prebrojati.  Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN? Zato je mene, dok sam bio "mali", zbunjivalo da kako se mogu prebrojati elementi skupa IN?  |
Vidis, nisam o tome nikad razmisljao na takav nacin, mozda bi stvarno brojiv bio sretniji naziv, ali s druge strane nije li svaki skup koji se moze dobro urediti brojiv   |
Sure thing.  Ono "brojiv" sam dao samo kao primjer... Ono "brojiv" sam dao samo kao primjer... 
Mozda bi to mogli zvati "prirodan skup"?  Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti... Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti...  Ipak sam se probudio prije samo 20ak minuta... Ipak sam se probudio prije samo 20ak minuta...   
Besides, nece nitko poslusati nase prijedloge odavde, pa nam se bas i ne isplati trud oko trazenja pogodnijeg imena.  Mene bi zanimalo odakle taj naziv "prebrojiv" koji se ocito koristi i u drugim jezicima... Mene bi zanimalo odakle taj naziv "prebrojiv" koji se ocito koristi i u drugim jezicima... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
gina
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 1:10 čet, 5. 8. 2004 Naslov: Postano: 1:10 čet, 5. 8. 2004 Naslov: |
    |
|
|
[quote="vsego"]Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i [b]IZ[/b]brojati (sve) njegove elemente... 8)[/quote]
Nista lakse :prodike: Prvi element brojis 1/2 minute, drugi 1/4 minute, treci 1/8... Za minutu si gotov :wacky:
| vsego (napisa): | Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i IZbrojati (sve) njegove elemente...  |
Nista lakse  Prvi element brojis 1/2 minute, drugi 1/4 minute, treci 1/8... Za minutu si gotov Prvi element brojis 1/2 minute, drugi 1/4 minute, treci 1/8... Za minutu si gotov 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 9:35 pet, 27. 8. 2004 Naslov: Postano: 9:35 pet, 27. 8. 2004 Naslov: |
    |
|
|
[quote="vsego"][quote="mdoko"]Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N.[/quote]
Mislim da vise zbunjuje sam naziv [b]prebrojiv[/b]. :? To aludira da se njegovi elementi mogu [b]prebrojati[/b]. :-s[/quote]
Pa i mogu... nisi li još primijetio da se matematičari obično vole ponašati kao da imaju beskonačno mnogo vremena na raspolaganju? :-)
(Pa čak i math-računarci... pogledaj implementaciju Turingovih strojeva, npr.; )
[quote]Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i [b]IZ[/b]brojati (sve) njegove elemente... 8) Mozda bi "[i]brojiv[/i]" bio sretniji naziv? :lol: ;)[/quote]
Samo se ti smij... vidio sam ja i bizarnijih. :-)
| vsego (napisa): | | mdoko (napisa): | | Ono sto moze stvoriti zabunu je to sto se ponekad kaze da je A prebrojiv ako je A konacan, ili A ~ |N. |
Mislim da vise zbunjuje sam naziv prebrojiv.  To aludira da se njegovi elementi mogu prebrojati. To aludira da se njegovi elementi mogu prebrojati.  |
Pa i mogu... nisi li još primijetio da se matematičari obično vole ponašati kao da imaju beskonačno mnogo vremena na raspolaganju? 
(Pa čak i math-računarci... pogledaj implementaciju Turingovih strojeva, npr.; )
| Citat: | Zapravo, ako je skup (beskonacno) prebrojiv, onda mozemo brojati, ali ne i IZbrojati (sve) njegove elemente...  Mozda bi "brojiv" bio sretniji naziv? Mozda bi "brojiv" bio sretniji naziv?   |
Samo se ti smij... vidio sam ja i bizarnijih. 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 9:54 pet, 27. 8. 2004 Naslov: Postano: 9:54 pet, 27. 8. 2004 Naslov: |
    |
|
|
[quote="mdoko"]nije li svaki skup koji se moze dobro urediti brojiv :grebgreb: :?:[/quote]
IMO, nije.
"brojanje" je koncept koji bi u sebi trebao nositi reprezentaciju prirodnih brojeva, odnosno konačnih ordinala. Oni su izgrađeni polaskom od 0 i operacijom sljedbenika - oba ta pojma imaju jasne ekvivalente u brojenju (to što su ljudi lijeni, pa ne broje od 0 nego od 1 , je već druga priča: ).
Općeniti ordinali, reprezentanti proizvoljnih dobro uređenih skupova, izgrađeni su pomoću još jedne operacije - unije, odnosno supremuma - koja baš i nema (čini mi se) neku prirodnu interpretaciju pri brojanju.
Konkretno, kako bi zapravo brojao [latex]\omega+1[/latex] ? Odnosno, što s njegovim zadnjim elementom? U ovom slučaju možeš ga prebrojati na početku, ali npr. kod [latex]\omega_2[/latex] ne možeš ništa takvoga učiniti.
(Osim, naravno, ako pod "brojiv" misliš da možeš samo _početi_ brojati dio tog skupa... no onda je svaki skup koji ima prebrojiv podskup, brojiv.: )
| mdoko (napisa): | nije li svaki skup koji se moze dobro urediti brojiv   |
IMO, nije.
"brojanje" je koncept koji bi u sebi trebao nositi reprezentaciju prirodnih brojeva, odnosno konačnih ordinala. Oni su izgrađeni polaskom od 0 i operacijom sljedbenika - oba ta pojma imaju jasne ekvivalente u brojenju (to što su ljudi lijeni, pa ne broje od 0 nego od 1 , je već druga priča: ).
Općeniti ordinali, reprezentanti proizvoljnih dobro uređenih skupova, izgrađeni su pomoću još jedne operacije - unije, odnosno supremuma - koja baš i nema (čini mi se) neku prirodnu interpretaciju pri brojanju.
Konkretno, kako bi zapravo brojao 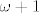 ? Odnosno, što s njegovim zadnjim elementom? U ovom slučaju možeš ga prebrojati na početku, ali npr. kod ? Odnosno, što s njegovim zadnjim elementom? U ovom slučaju možeš ga prebrojati na početku, ali npr. kod 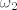 ne možeš ništa takvoga učiniti. ne možeš ništa takvoga učiniti.
(Osim, naravno, ako pod "brojiv" misliš da možeš samo _početi_ brojati dio tog skupa... no onda je svaki skup koji ima prebrojiv podskup, brojiv.: )
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 10:03 pet, 27. 8. 2004 Naslov: Postano: 10:03 pet, 27. 8. 2004 Naslov: |
    |
|
|
[quote="vsego"]Mozda bi to mogli zvati "[i]prirodan skup[/i]"? :-k Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti... :|[/quote]
Ja se također ne mogu sjetiti. Moguće je i da nije potrošen. :-)
No moj notacijski purizam se mršti na ovaj naziv, zbog malog tehničkog problema... naime, [latex]\aleph_0[/latex] bi onda bio prirodan skup, i očito je broj, ali inheritance je narušen: brojevi su skupovi, ali [latex]\aleph_0[/latex] nije prirodan broj. (Naravno, ima takvih slučajeva posvuda po matematici... parcijalne funkcije nisu funkcije, nultočke nisu točke,... ali nije da ih volim.)
[quote]Besides, nece nitko poslusati nase prijedloge odavde, pa nam se bas i ne isplati trud oko trazenja pogodnijeg imena. :|[/quote]
Ne budi tako siguran... čak i moja notacija povremeno završi na nekom "poluslužbenom" mjestu. ;-)
[quote] Mene bi zanimalo odakle taj naziv "[i]prebrojiv[/i]" koji se ocito koristi i u drugim jezicima... :-k[/quote]
Gore (u odgovoru mdoku) piše ponešto. :-)
| vsego (napisa): | Mozda bi to mogli zvati "prirodan skup"?  Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti... Nekako mi zvoni da je naziv potrosen na nesto, ali ne mogu se sjetiti...  |
Ja se također ne mogu sjetiti. Moguće je i da nije potrošen. 
No moj notacijski purizam se mršti na ovaj naziv, zbog malog tehničkog problema... naime, 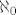 bi onda bio prirodan skup, i očito je broj, ali inheritance je narušen: brojevi su skupovi, ali bi onda bio prirodan skup, i očito je broj, ali inheritance je narušen: brojevi su skupovi, ali 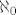 nije prirodan broj. (Naravno, ima takvih slučajeva posvuda po matematici... parcijalne funkcije nisu funkcije, nultočke nisu točke,... ali nije da ih volim.) nije prirodan broj. (Naravno, ima takvih slučajeva posvuda po matematici... parcijalne funkcije nisu funkcije, nultočke nisu točke,... ali nije da ih volim.)
| Citat: | Besides, nece nitko poslusati nase prijedloge odavde, pa nam se bas i ne isplati trud oko trazenja pogodnijeg imena.  |
Ne budi tako siguran... čak i moja notacija povremeno završi na nekom "poluslužbenom" mjestu. 
| Citat: | Mene bi zanimalo odakle taj naziv "prebrojiv" koji se ocito koristi i u drugim jezicima...  |
Gore (u odgovoru mdoku) piše ponešto. 
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 10:15 pet, 27. 8. 2004 Naslov: Postano: 10:15 pet, 27. 8. 2004 Naslov: |
    |
|
|
:OT:
[quote="veky"] .... [/quote]
:valovi:
welcome back, vec sam mislio da ti se nije sta desilo :D


welcome back, vec sam mislio da ti se nije sta desilo 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
|









