| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 8:26 sub, 28. 8. 2004 Naslov: Fundamentalan teorem za integrale Postano: 8:26 sub, 28. 8. 2004 Naslov: Fundamentalan teorem za integrale |
    |
|
|
[color=green]Fundamentalan teorem:
Pretpostavke: f:I->IR,I podskup IR te I je otvoreni interval.
Doprinosi teorema:
-a,b@I,a<b f je (R)-integrabilna na [a,b]
-f ima primitivnu funkciju na I
-a<b,G primitivna funkcija sa f na I tada vrijedi: aSb f(x)dx=G(b)-G(a)[/color]
(Napomena: aSb je oznaka za određeni integral u granicama od 'a' do 'b'.)
Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ?
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema.
Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema.
Fundamentalan teorem:
Pretpostavke: f:I→IR,I podskup IR te I je otvoreni interval.
Doprinosi teorema:
-a,b@I,a<b f je (R)-integrabilna na [a,b]
-f ima primitivnu funkciju na I
-a<b,G primitivna funkcija sa f na I tada vrijedi: aSb f(x)dx=G(b)-G(a)
(Napomena: aSb je oznaka za određeni integral u granicama od 'a' do 'b'.)
Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ?
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema.
Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 9:12 sub, 28. 8. 2004 Naslov: Re: Fundamentalan teorem za integrale Postano: 9:12 sub, 28. 8. 2004 Naslov: Re: Fundamentalan teorem za integrale |
    |
|
|
[code:1]Fundamentalan teorem:
Pretpostavke: f:I->IR,I podskup IR te I je otvoreni interval.
Doprinosi teorema:
-a,b@I,a<b f je (R)-integrabilna na [a,b]
-f ima primitivnu funkciju na I
-a<b,G primitivna funkcija sa f na I tada vrijedi: aSb f(x)dx=G(b)-G(a)
(Napomena: aSb je oznaka za određeni integral u granicama od 'a' do 'b'.)[/code:1]
[quote="Vincent Van Ear"]Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ?
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema.[/quote]
Ovako samo na prvi pogled: Riemannov teorem (i Newton-Leibnitzov, i persume) se obraca neprekidnim fjama na segmentu(ako nisam pobrkao loncice). Sa druge strane ovdje nemamo segment nego otvoreni interval.
[quote="Vincent Van Ear"]Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema.[/quote]
...a kako si mogao svjedociti kroz nekoliko teorema kroz koje si prosao u poslijednje vrijeme ;), taj skok sa segmenta na interval uopce nije trivijalan
PS pretpostavio sam da je f neprekidna fja iako to nisi napisao :-k
| Kod: | Fundamentalan teorem:
Pretpostavke: f:I->IR,I podskup IR te I je otvoreni interval.
Doprinosi teorema:
-a,b@I,a<b f je (R)-integrabilna na [a,b]
-f ima primitivnu funkciju na I
-a<b,G primitivna funkcija sa f na I tada vrijedi: aSb f(x)dx=G(b)-G(a)
(Napomena: aSb je oznaka za određeni integral u granicama od 'a' do 'b'.) |
| Vincent Van Ear (napisa): | Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ?
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema. |
Ovako samo na prvi pogled: Riemannov teorem (i Newton-Leibnitzov, i persume) se obraca neprekidnim fjama na segmentu(ako nisam pobrkao loncice). Sa druge strane ovdje nemamo segment nego otvoreni interval.
| Vincent Van Ear (napisa): | | Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema. |
...a kako si mogao svjedociti kroz nekoliko teorema kroz koje si prosao u poslijednje vrijeme  , taj skok sa segmenta na interval uopce nije trivijalan , taj skok sa segmenta na interval uopce nije trivijalan
PS pretpostavio sam da je f neprekidna fja iako to nisi napisao 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 10:04 sub, 28. 8. 2004 Naslov: Re: Fundamentalan teorem za integrale Postano: 10:04 sub, 28. 8. 2004 Naslov: Re: Fundamentalan teorem za integrale |
    |
|
|
[quote="Vincent Van Ear"][color=green]Fundamentalan teorem:
Pretpostavke: [latex]f:I\to R, I[/latex] je otvoreni interval.
Doprinosi teorema:
- [latex]a,b\in I, a<b\quad f[/latex] je R-integrabilna na [latex][a,b][/latex]
- [latex]f[/latex] ima primitivnu funkciju na [latex]I[/latex]
- [latex]G[/latex] primitivna funkcija sa [latex]f[/latex] na [latex]I[/latex] tada vrijedi: [latex]\displaystyle\int_a^b f(x)dx=G(b)-G(a)[/latex][/color]
Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ?[/quote]
Naravno da ne smiju. Pa zar da krse copyright (odnosno autorska prava) ljudi koji su ih rekli. Pa bi onda jos netko iskoristio Pitagorin teorem kao dio nekog veceg teorema... grozno.. :)
Usput, ovo nije teorem, jer tvrdnja ne vrijedi za [latex]f:x\in\langle e,\pi\rangle
\mapsto\left\{\matrix{1,& x\in Q\cr 0,&\hbox{\rm ina\v ce}\cr}\right.[/latex].
[quote="Vincent Van Ear"]
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema.
Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema.[/quote]
Point neceg kao [b]osnovnog[/b] teorema jest da je u njemu je navedena lista svega sto se moze uciniti sa minimalno moguce pretpostavki, tj. ako pretpostavimo da baratamo sa funkcijom sa konacno mnogo prekida(dapace, prebrojivo mnogo), onda ti ovaj teorem kaze jako puno. [i]Kod teorema je bitnije da [b]nesto[/b] kazu, nego tko je rekao, tj. preko kojih tvrdnji to trivijalno slijedi.[/i]
estetsko pitanje za TeX - bi li bilo moguce da se baselineovi zrihtaju, tj. da se TeX output lijepo slaze u tekst?
'ave fun!
Sinisa
| Vincent Van Ear (napisa): | Fundamentalan teorem:
Pretpostavke: 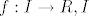 je otvoreni interval. je otvoreni interval.
Doprinosi teorema:
- 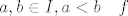 je R-integrabilna na je R-integrabilna na 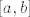
-  ima primitivnu funkciju na ima primitivnu funkciju na 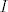
- 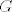 primitivna funkcija sa primitivna funkcija sa  na na 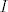 tada vrijedi: tada vrijedi: 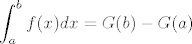
Moje pitanje:
Zar smiju ''tuđi'' teoremi ''krasti'' doprinose nekih drugih teorema ? |
Naravno da ne smiju. Pa zar da krse copyright (odnosno autorska prava) ljudi koji su ih rekli. Pa bi onda jos netko iskoristio Pitagorin teorem kao dio nekog veceg teorema... grozno.. 
Usput, ovo nije teorem, jer tvrdnja ne vrijedi za 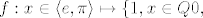 . .
| Vincent Van Ear (napisa): |
Prvi doprinos je posljedica Reimanovog teorema,a drugi je posljedica opet jednog teorema.
Jeli to naš profesor samovoljno ubacio u ovaj teorem te doprinose kako bi na usmenom bilo što zanimljivije,odnosno,svjestan je pita li te fundamentalan teorem pitao te još minimalno dva teorema. |
Point neceg kao osnovnog teorema jest da je u njemu je navedena lista svega sto se moze uciniti sa minimalno moguce pretpostavki, tj. ako pretpostavimo da baratamo sa funkcijom sa konacno mnogo prekida(dapace, prebrojivo mnogo), onda ti ovaj teorem kaze jako puno. Kod teorema je bitnije da nesto kazu, nego tko je rekao, tj. preko kojih tvrdnji to trivijalno slijedi.
estetsko pitanje za TeX - bi li bilo moguce da se baselineovi zrihtaju, tj. da se TeX output lijepo slaze u tekst?
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 10:57 sub, 28. 8. 2004 Naslov: Postano: 10:57 sub, 28. 8. 2004 Naslov: |
    |
|
|
[quote]Ovako samo na prvi pogled: Riemannov teorem (i Newton-Leibnitzov, i persume) se obraca neprekidnim fjama na segmentu(ako nisam pobrkao loncice). Sa druge strane ovdje nemamo segment nego otvoreni interval.[/quote]
Ok,ali poprilično je jasno da uzmem li dvije točke iz otv.intervala da zaključak što slijedi je posljedica Reimana.
Mah... :wink:
[quote]PS pretpostavio sam da je f neprekidna fja iako to nisi napisao[/quote]
Je-je,imam feler-ČINU!
:)
[quote]Naravno da ne smiju. Pa zar da krse copyright (odnosno autorska prava) ljudi koji su ih rekli. Pa bi onda jos netko iskoristio Pitagorin teorem kao dio nekog veceg teorema... grozno.. [/quote]
=))
Čuj glavno da je navedeno ime tvorca,Pitagora je rekao(yeah right):koristite moj teorem ali bez moga loga-imena ja bum vas sve tužil,to je otišlo toliko daleko da sam čuo(yeah right!) da je jednoga sljedbenika umakao u bazen dok ovaj nije postao mlohav ko' pijanac na ispumpavanju.
:wink:
| Citat: | | Ovako samo na prvi pogled: Riemannov teorem (i Newton-Leibnitzov, i persume) se obraca neprekidnim fjama na segmentu(ako nisam pobrkao loncice). Sa druge strane ovdje nemamo segment nego otvoreni interval. |
Ok,ali poprilično je jasno da uzmem li dvije točke iz otv.intervala da zaključak što slijedi je posljedica Reimana.
Mah... 
| Citat: | | PS pretpostavio sam da je f neprekidna fja iako to nisi napisao |
Je-je,imam feler-ČINU!

| Citat: | | Naravno da ne smiju. Pa zar da krse copyright (odnosno autorska prava) ljudi koji su ih rekli. Pa bi onda jos netko iskoristio Pitagorin teorem kao dio nekog veceg teorema... grozno.. |
=))
Čuj glavno da je navedeno ime tvorca,Pitagora je rekao(yeah right):koristite moj teorem ali bez moga loga-imena ja bum vas sve tužil,to je otišlo toliko daleko da sam čuo(yeah right!) da je jednoga sljedbenika umakao u bazen dok ovaj nije postao mlohav ko' pijanac na ispumpavanju.

_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 11:13 sub, 28. 8. 2004 Naslov: Postano: 11:13 sub, 28. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Ok,ali poprilično je jasno da uzmem li dvije točke iz otv.intervala da zaključak što slijedi je posljedica Reimana.
Mah... :wink: [/quote]
Mozebit "jasno" ali nije "isto". To sto je nesto jednostavno (iako opet ne potpuno trivijalno) dokazivo iz neceg drugog ne znaci da su te stvari "iste" :roll:
Dapace :!: priroda ta dva teorema je potpuno drugacija i predstavlja jedan znatan skok sa definicije integrala kakvu ste obradili pocetkom semestra. Sirenje neke teorije sa otvorenih na zatvorene skupove i obratno je bitan i pocesto, barem tehnicki, vrlo netrivijalan korak :evil: sijeti se samo sto ucinismo od segmenta za potrebe sirenja definicije neprekidnosti na segmente :!:
[quote="cinik"]estetsko pitanje za TeX - bi li bilo moguce da se baselineovi zrihtaju, tj. da se TeX output lijepo slaze u tekst?[/quote]
[url=http://degiorgi.math.hr/forum/viewtopic.php?t=2474]Pitaj negdje gdje ce te vsego ugledati ;)[/url]
| Vincent Van Ear (napisa): | Ok,ali poprilično je jasno da uzmem li dvije točke iz otv.intervala da zaključak što slijedi je posljedica Reimana.
Mah...  |
Mozebit "jasno" ali nije "isto". To sto je nesto jednostavno (iako opet ne potpuno trivijalno) dokazivo iz neceg drugog ne znaci da su te stvari "iste" 
Dapace  priroda ta dva teorema je potpuno drugacija i predstavlja jedan znatan skok sa definicije integrala kakvu ste obradili pocetkom semestra. Sirenje neke teorije sa otvorenih na zatvorene skupove i obratno je bitan i pocesto, barem tehnicki, vrlo netrivijalan korak priroda ta dva teorema je potpuno drugacija i predstavlja jedan znatan skok sa definicije integrala kakvu ste obradili pocetkom semestra. Sirenje neke teorije sa otvorenih na zatvorene skupove i obratno je bitan i pocesto, barem tehnicki, vrlo netrivijalan korak  sijeti se samo sto ucinismo od segmenta za potrebe sirenja definicije neprekidnosti na segmente sijeti se samo sto ucinismo od segmenta za potrebe sirenja definicije neprekidnosti na segmente 
| cinik (napisa): | | estetsko pitanje za TeX - bi li bilo moguce da se baselineovi zrihtaju, tj. da se TeX output lijepo slaze u tekst? |
Pitaj negdje gdje ce te vsego ugledati 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|





