| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
aj_ca_volin_te
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
|
|
| [Vrh] |
|
nicki minaj
Forumaš(ica)

Pridružen/a: 15. 01. 2012. (02:34:45)
Postovi: (11)16
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:28 pet, 22. 6. 2012 Naslov: Postano: 0:28 pet, 22. 6. 2012 Naslov: |
    |
|
|
[quote="slonic~tonic"]moze mi netko pomoci, kako razviti eksponencijalnu funkciju u Taylorov red??[/quote]
Funkcija se može (pod nekim uvjetima) razviti u Taylorov red [i]oko neke točke c[/i]. Nije nebitan taj dio "oko neke točke c" jer definicija (a kasnije i konvergencija) tog reda ovisi o točki c.
Znači, neka je [tex]I\subset\mathbb{R}[/tex] otvoren interval, c neka je bilo koja točka tog intervala, a [tex]f\colon I \to \mathbb{R}[/tex] neka je zadana s [tex]f(x)=a^x[/tex], za [tex]a\in\left\langle 0,\infty\right\rangle\setminus\{1\}.[/tex]
Da bi funkciju f mogli razviti u Taylorov red oko točke c, ona mora biti klase [tex]C^\infty[/tex] na intervalu I. Pomoću logaritamske derivacije izračunamo da je [tex]f'(x)=a^x\ln a[/tex], a ako još jednom deriviramo dobijemo [tex]f''(x)=a^x(\ln a)^2=f'(x)\ln a[/tex]. Očito je onda [tex]f'''(x)=f''(x)\ln a=a^x(\ln a)^3[/tex] pa zaključujemo kako n-ta derivacija mora biti jednaka [tex]f^{(n)}(x)=a^x(\ln a)^n[/tex] i to još formalno dokažemo indukcijom. To vrijedi za svaki x iz I pa je Taylorov red funkcije f oko točke c jednak [dtex]a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n.[/dtex]
Ostaje pokazati da [tex]a^x[/tex] konvergira tom redu. Iskoristiti ćemo teorem 6.13. Neka je [tex]\delta > 0[/tex] i [tex]a>1[/tex] (slučaj 0<a<1 pokaže se analogno). Tada, za [tex]x<c+\delta[/tex] vrijedi [tex]a^x<a^{c+\delta}[/tex] pa je [tex]a^x(\ln a)^n<a^{c+\delta}(\ln a)^n[/tex].
Neka je [tex]n_0=1, C=a^{c+\delta}[/tex] i [tex]M=\ln a.[/tex]. Tada za svaki [tex]n\geq n_0[/tex] vrijedi
[dtex]|f^{(n)}(x)|=a^x(\ln{a})^n<a^{c+\delta}(\ln a)^n=CM^n<CM^nn!,[/dtex]
za svaki [tex]x\in I'=\left\langle c-\delta, c+\delta\right\rangle\cap I[/tex], a to znači da je
[dtex]a^x=a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n,\textrm{ za svaki }x\in\left\langle c-\frac 1M, c+\frac 1M\right\rangle\cap I'[/dtex]
| slonic~tonic (napisa): | | moze mi netko pomoci, kako razviti eksponencijalnu funkciju u Taylorov red?? |
Funkcija se može (pod nekim uvjetima) razviti u Taylorov red oko neke točke c. Nije nebitan taj dio "oko neke točke c" jer definicija (a kasnije i konvergencija) tog reda ovisi o točki c.
Znači, neka je [tex]I\subset\mathbb{R}[/tex] otvoren interval, c neka je bilo koja točka tog intervala, a [tex]f\colon I \to \mathbb{R}[/tex] neka je zadana s [tex]f(x)=a^x[/tex], za [tex]a\in\left\langle 0,\infty\right\rangle\setminus\{1\}.[/tex]
Da bi funkciju f mogli razviti u Taylorov red oko točke c, ona mora biti klase [tex]C^\infty[/tex] na intervalu I. Pomoću logaritamske derivacije izračunamo da je [tex]f'(x)=a^x\ln a[/tex], a ako još jednom deriviramo dobijemo [tex]f''(x)=a^x(\ln a)^2=f'(x)\ln a[/tex]. Očito je onda [tex]f'''(x)=f''(x)\ln a=a^x(\ln a)^3[/tex] pa zaključujemo kako n-ta derivacija mora biti jednaka [tex]f^{(n)}(x)=a^x(\ln a)^n[/tex] i to još formalno dokažemo indukcijom. To vrijedi za svaki x iz I pa je Taylorov red funkcije f oko točke c jednak [dtex]a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n.[/dtex]
Ostaje pokazati da [tex]a^x[/tex] konvergira tom redu. Iskoristiti ćemo teorem 6.13. Neka je [tex]\delta > 0[/tex] i [tex]a>1[/tex] (slučaj 0<a<1 pokaže se analogno). Tada, za [tex]x<c+\delta[/tex] vrijedi [tex]a^x<a^{c+\delta}[/tex] pa je [tex]a^x(\ln a)^n<a^{c+\delta}(\ln a)^n[/tex].
Neka je [tex]n_0=1, C=a^{c+\delta}[/tex] i [tex]M=\ln a.[/tex]. Tada za svaki [tex]n\geq n_0[/tex] vrijedi
[dtex]|f^{(n)}(x)|=a^x(\ln{a})^n<a^{c+\delta}(\ln a)^n=CM^n<CM^nn!,[/dtex]
za svaki [tex]x\in I'=\left\langle c-\delta, c+\delta\right\rangle\cap I[/tex], a to znači da je
[dtex]a^x=a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n,\textrm{ za svaki }x\in\left\langle c-\frac 1M, c+\frac 1M\right\rangle\cap I'[/dtex]
_________________
The Dude Abides
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
 Postano: 18:36 pet, 22. 6. 2012 Naslov: Postano: 18:36 pet, 22. 6. 2012 Naslov: |
    |
|
|
[quote="goranm"][quote="slonic~tonic"]moze mi netko pomoci, kako razviti eksponencijalnu funkciju u Taylorov red??[/quote]
Funkcija se može (pod nekim uvjetima) razviti u Taylorov red [i]oko neke točke c[/i]. Nije nebitan taj dio "oko neke točke c" jer definicija (a kasnije i konvergencija) tog reda ovisi o točki c.
Znači, neka je [tex]I\subset\mathbb{R}[/tex] otvoren interval, c neka je bilo koja točka tog intervala, a [tex]f\colon I \to \mathbb{R}[/tex] neka je zadana s [tex]f(x)=a^x[/tex], za [tex]a\in\left\langle 0,\infty\right\rangle\setminus\{1\}.[/tex]
Da bi funkciju f mogli razviti u Taylorov red oko točke c, ona mora biti klase [tex]C^\infty[/tex] na intervalu I. Pomoću logaritamske derivacije izračunamo da je [tex]f'(x)=a^x\ln a[/tex], a ako još jednom deriviramo dobijemo [tex]f''(x)=a^x(\ln a)^2=f'(x)\ln a[/tex]. Očito je onda [tex]f'''(x)=f''(x)\ln a=a^x(\ln a)^3[/tex] pa zaključujemo kako n-ta derivacija mora biti jednaka [tex]f^{(n)}(x)=a^x(\ln a)^n[/tex] i to još formalno dokažemo indukcijom. To vrijedi za svaki x iz I pa je Taylorov red funkcije f oko točke c jednak [dtex]a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n.[/dtex]
Ostaje pokazati da [tex]a^x[/tex] konvergira tom redu. Iskoristiti ćemo teorem 6.13. Neka je [tex]\delta > 0[/tex] i [tex]a>1[/tex] (slučaj 0<a<1 pokaže se analogno). Tada, za [tex]x<c+\delta[/tex] vrijedi [tex]a^x<a^{c+\delta}[/tex] pa je [tex]a^x(\ln a)^n<a^{c+\delta}(\ln a)^n[/tex].
Neka je [tex]n_0=1, C=a^{c+\delta}[/tex] i [tex]M=\ln a.[/tex]. Tada za svaki [tex]n\geq n_0[/tex] vrijedi
[dtex]|f^{(n)}(x)|=a^x(\ln{a})^n<a^{c+\delta}(\ln a)^n=CM^n<CM^nn!,[/dtex]
za svaki [tex]x\in I'=\left\langle c-\delta, c+\delta\right\rangle\cap I[/tex], a to znači da je
[dtex]a^x=a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n,\textrm{ za svaki }x\in\left\langle c-\frac 1M, c+\frac 1M\right\rangle\cap I'[/dtex][/quote]
hvala puno!!! :)
jos samo da pitam, za svaki slucaj, analogno je kad je a = e??
| goranm (napisa): | | slonic~tonic (napisa): | | moze mi netko pomoci, kako razviti eksponencijalnu funkciju u Taylorov red?? |
Funkcija se može (pod nekim uvjetima) razviti u Taylorov red oko neke točke c. Nije nebitan taj dio "oko neke točke c" jer definicija (a kasnije i konvergencija) tog reda ovisi o točki c.
Znači, neka je [tex]I\subset\mathbb{R}[/tex] otvoren interval, c neka je bilo koja točka tog intervala, a [tex]f\colon I \to \mathbb{R}[/tex] neka je zadana s [tex]f(x)=a^x[/tex], za [tex]a\in\left\langle 0,\infty\right\rangle\setminus\{1\}.[/tex]
Da bi funkciju f mogli razviti u Taylorov red oko točke c, ona mora biti klase [tex]C^\infty[/tex] na intervalu I. Pomoću logaritamske derivacije izračunamo da je [tex]f'(x)=a^x\ln a[/tex], a ako još jednom deriviramo dobijemo [tex]f''(x)=a^x(\ln a)^2=f'(x)\ln a[/tex]. Očito je onda [tex]f'''(x)=f''(x)\ln a=a^x(\ln a)^3[/tex] pa zaključujemo kako n-ta derivacija mora biti jednaka [tex]f^{(n)}(x)=a^x(\ln a)^n[/tex] i to još formalno dokažemo indukcijom. To vrijedi za svaki x iz I pa je Taylorov red funkcije f oko točke c jednak [dtex]a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n.[/dtex]
Ostaje pokazati da [tex]a^x[/tex] konvergira tom redu. Iskoristiti ćemo teorem 6.13. Neka je [tex]\delta > 0[/tex] i [tex]a>1[/tex] (slučaj 0<a<1 pokaže se analogno). Tada, za [tex]x<c+\delta[/tex] vrijedi [tex]a^x<a^{c+\delta}[/tex] pa je [tex]a^x(\ln a)^n<a^{c+\delta}(\ln a)^n[/tex].
Neka je [tex]n_0=1, C=a^{c+\delta}[/tex] i [tex]M=\ln a.[/tex]. Tada za svaki [tex]n\geq n_0[/tex] vrijedi
[dtex]|f^{(n)}(x)|=a^x(\ln{a})^n<a^{c+\delta}(\ln a)^n=CM^n<CM^nn!,[/dtex]
za svaki [tex]x\in I'=\left\langle c-\delta, c+\delta\right\rangle\cap I[/tex], a to znači da je
[dtex]a^x=a^c\cdot \sum_{n=0}^\infty \frac{(\ln a)^n}{n!}(x-c)^n,\textrm{ za svaki }x\in\left\langle c-\frac 1M, c+\frac 1M\right\rangle\cap I'[/dtex] |
hvala puno!!! 
jos samo da pitam, za svaki slucaj, analogno je kad je a = e??
_________________
Lakše je naučiti matematiku nego raditi bez nje.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
aeternitas
Forumaš(ica)

Pridružen/a: 27. 10. 2012. (17:45:39)
Postovi: (3)16
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
aeternitas
Forumaš(ica)

Pridružen/a: 27. 10. 2012. (17:45:39)
Postovi: (3)16
|
 Postano: 16:11 pet, 31. 5. 2013 Naslov: Postano: 16:11 pet, 31. 5. 2013 Naslov: |
    |
|
|
[quote="matkec"]Ovaj prvi rastavi na parcijalne razlomke i raspiši prvih par članova. Vidjet ćeš kako ti se članovi krate.
Ovaj drugi mi je neka poznata fora, ali se trenutno ne mogu sjetiti... :/[/quote]
hvala za prvi, skužih :)
drugi možda da usporedim prvo sin s nekom funkcijom za koju znam da konv/div, pa idem na usporedni kriterij \lim \frac{a_{n}}{b_{n}} i onda zaključujem konvergira li ili dirvergira
(s tim da mi je \lim \frac{sinx}{x} = 1, pri čemu mi je x ovaj izraz u sinusu)
to mi je sad palo na pamet, ne znam drži li vodu :oops:
| matkec (napisa): | Ovaj prvi rastavi na parcijalne razlomke i raspiši prvih par članova. Vidjet ćeš kako ti se članovi krate.
Ovaj drugi mi je neka poznata fora, ali se trenutno ne mogu sjetiti...  |
hvala za prvi, skužih 
drugi možda da usporedim prvo sin s nekom funkcijom za koju znam da konv/div, pa idem na usporedni kriterij \lim \frac{a_{n}}{b_{n}} i onda zaključujem konvergira li ili dirvergira
(s tim da mi je \lim \frac{sinx}{x} = 1, pri čemu mi je x ovaj izraz u sinusu)
to mi je sad palo na pamet, ne znam drži li vodu 
_________________
Go down deep enough into anything and you will find mathematics.
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
 Postano: 21:03 pet, 31. 5. 2013 Naslov: Postano: 21:03 pet, 31. 5. 2013 Naslov: |
    |
|
|
Ma mislio sam da je ta suma izračunljiva. No, ili ja ne znam izračunati kolika je ta suma, ili je za suma stvarno ne izračunljiva. Pitao sam wolframa, on kaže da je suma jednaka 1.5432996823296632. Mislio sam stoga da red konvergira ka pi/2, ali je razlika prevelika, ne bi wolfram tolko fulo.
Ali ako se u zadatku traži samo provjeriti konvergira li red, tada je ovaj tvoj način dobar. Po usporednom kriteriju, treba provjeriti konvergira li red [latex] \displaystyle \sum_{n=1}^{\infty } \frac{2}{n^{2}+n+1} [/latex], no taj red lako ograničiš s redom [latex] \displaystyle \sum_{n=1}^{\infty } \frac{2}{n^{2}} [/latex].
Ma mislio sam da je ta suma izračunljiva. No, ili ja ne znam izračunati kolika je ta suma, ili je za suma stvarno ne izračunljiva. Pitao sam wolframa, on kaže da je suma jednaka 1.5432996823296632. Mislio sam stoga da red konvergira ka pi/2, ali je razlika prevelika, ne bi wolfram tolko fulo.
Ali ako se u zadatku traži samo provjeriti konvergira li red, tada je ovaj tvoj način dobar. Po usporednom kriteriju, treba provjeriti konvergira li red 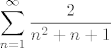 , no taj red lako ograničiš s redom , no taj red lako ograničiš s redom 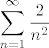 . .
|
|
| [Vrh] |
|
aeternitas
Forumaš(ica)

Pridružen/a: 27. 10. 2012. (17:45:39)
Postovi: (3)16
|
 Postano: 12:42 sub, 1. 6. 2013 Naslov: Postano: 12:42 sub, 1. 6. 2013 Naslov: |
    |
|
|
[quote="matkec"]Ma mislio sam da je ta suma izračunljiva. No, ili ja ne znam izračunati kolika je ta suma, ili je za suma stvarno ne izračunljiva. Pitao sam wolframa, on kaže da je suma jednaka 1.5432996823296632. Mislio sam stoga da red konvergira ka pi/2, ali je razlika prevelika, ne bi wolfram tolko fulo.
Ali ako se u zadatku traži samo provjeriti konvergira li red, tada je ovaj tvoj način dobar. Po usporednom kriteriju, treba provjeriti konvergira li red [latex] \displaystyle \sum_{n=1}^{\infty } \frac{2}{n^{2}+n+1} [/latex], no taj red lako ograničiš s redom [latex] \displaystyle \sum_{n=1}^{\infty } \frac{2}{n^{2}} [/latex].[/quote]
Nisam precizirala, da upravo se radi o ispitivanju konvergencije, onda je okej. :)
Hvala ti.
| matkec (napisa): | Ma mislio sam da je ta suma izračunljiva. No, ili ja ne znam izračunati kolika je ta suma, ili je za suma stvarno ne izračunljiva. Pitao sam wolframa, on kaže da je suma jednaka 1.5432996823296632. Mislio sam stoga da red konvergira ka pi/2, ali je razlika prevelika, ne bi wolfram tolko fulo.
Ali ako se u zadatku traži samo provjeriti konvergira li red, tada je ovaj tvoj način dobar. Po usporednom kriteriju, treba provjeriti konvergira li red 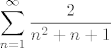 , no taj red lako ograničiš s redom , no taj red lako ograničiš s redom 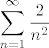 . . |
Nisam precizirala, da upravo se radi o ispitivanju konvergencije, onda je okej. 
Hvala ti.
_________________
Go down deep enough into anything and you will find mathematics.
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
tiborr
Forumaš(ica)
Pridružen/a: 23. 12. 2012. (18:54:28)
Postovi: (E)16
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
markann
Forumaš(ica)
Pridružen/a: 07. 10. 2013. (01:37:06)
Postovi: (1F)16
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
|
| [Vrh] |
|
|













