Dobro uređeni skupovi (objasnjenje gradiva)

[lucijana]

1.Koji od navedenih skupova je dobro uređen


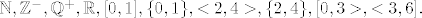
2.Neka je X potpuno uređen skup i Y uređen skup. Ako je 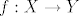uzlazna injekcija dokažite da je onda i f(X) potpuno uređen skup

Ako može netko detaljno raspisati ovaj drugi dokaz!!

Hvala unaprijed

[vsego]

1. Po definiciji. Ako zapnes na konkretnom primjeru, reci koji je i sto te tocno muci, pa cemo pomoci.

2. [tex]f:\ X \to f(X) \subseteq Y[/tex] je bijekcija. Neka je [tex]S \subseteq f(X)[/tex] neprazan. To znaci da je [tex]f^{-1}(S) \subseteq X[/tex], a [tex]X[/tex] je dobro uredjen, pa [tex]f^{-1}(S)[/tex] ima minimum [tex]m[/tex]. Iskoristi da je [tex]f[/tex] strogo uzlazna i pokazi da je [tex]f(m) = \min S[/tex]. Posto je [tex]S[/tex] proizvoljni podskup od [tex]f(X)[/tex], dokazano je sto se htjelo. Nije detaljno, ali ovdje pomazemo; ne rjesavamo umjesto drugih.

P.S. Bolje je koristiti [tex]...[/tex] nego [latex]...[/latex].

_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.

[lucijana]

Što se tiče prvog zadatka ja bih rekla da su dobro uređeni sljedeći:

[tex]\mathbb{N}[/tex] i [tex] \{0,1\} [/tex]

Ispravite me ako griješim..

hvala najljepša!

[mdoko]

[lucijana]

Da, i taj isto.

Hvala na pomoći!