| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 15:05 čet, 1. 6. 2006 Naslov: Postano: 15:05 čet, 1. 6. 2006 Naslov: |
    |
|
|
E[X]=Suma(n=0 do besk)P(X>n)
tada
E[min{X,Y}]=suma(n=0 do besk)P(min{X,Y}>n)=(ako je minimum od {X,Y} veci do n; tada je i X veci od n ,te Y veci od n,slijedi)=suma (n=0 do besk)P(X>n,Y>n)={nezavisnost}=suma(n=0 do besk)P(X>n)*P(Y>n).
E[X]=Suma(n=0 do besk)P(X>n)
tada
E[min{X,Y}]=suma(n=0 do besk)P(min{X,Y}>n)=(ako je minimum od {X,Y} veci do n; tada je i X veci od n ,te Y veci od n,slijedi)=suma (n=0 do besk)P(X>n,Y>n)={nezavisnost}=suma(n=0 do besk)P(X>n)*P(Y>n).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Gost
|
 Postano: 8:38 uto, 18. 7. 2006 Naslov: Postano: 8:38 uto, 18. 7. 2006 Naslov: |
    |
|
|
Bio bih zahvalan, ako bi netko mogao rjesiti sljedeci zadatak:
Neka su X1, X2, ... ,Xn nezavisne eksponencijalne slucajne varijable s istim ocekivanjem μ. Neka je M=min{ X1, X2, ... Xn }. Pokazite da je M eksponencijalno distribuirana. Koliko je ocekivanje od M?
Bio bih zahvalan, ako bi netko mogao rjesiti sljedeci zadatak:
Neka su X1, X2, ... ,Xn nezavisne eksponencijalne slucajne varijable s istim ocekivanjem μ. Neka je M=min{ X1, X2, ... Xn }. Pokazite da je M eksponencijalno distribuirana. Koliko je ocekivanje od M?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:01 pon, 15. 12. 2008 Naslov: Postano: 17:01 pon, 15. 12. 2008 Naslov: |
    |
|
|
kratko, ali slatko pitanje :D :
X i Y binomne sl var, [b]nisu nezavisne[/b],
X~B(n,p1) , Y~B(n,p2).
Kako izračunat E(XY) ?
Trebalo bi ispast n(n-1)*p1*p2
Hvala bilo kome na pomoći
kratko, ali slatko pitanje  : :
X i Y binomne sl var, nisu nezavisne,
X~B(n,p1) , Y~B(n,p2).
Kako izračunat E(XY) ?
Trebalo bi ispast n(n-1)*p1*p2
Hvala bilo kome na pomoći
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 21:45 pon, 15. 12. 2008 Naslov: Postano: 21:45 pon, 15. 12. 2008 Naslov: |
    |
|
|
Ne znam to pokazati, no izgleda mi to veoma sumnjivo, pretpostavimo da je doista tako, tj. da
[latex]\mathbb{E}[XY]=n(n-1)p_1p_2[/latex], gdje pripadne slucajne varijable imaju distribuciju koju si naveo. Izracunajmo stoga kovarijancu, dakle dobivamo;
[latex]Cox(X,Y)=\mathbb{E}[XY]-\mathbb{E}X\mathbb{E}Y=
n(n-1)p_1p_2-np_1np_2=np_1p_2\big((n-1)-n\big)=-np_1p_2[/latex]
odnosno slijedilo bi da su [latex]X,Y[/latex] nuzno negativno korelirane, a ne mora biti tako!
Ispravi me ako grijesim.
Ne znam to pokazati, no izgleda mi to veoma sumnjivo, pretpostavimo da je doista tako, tj. da
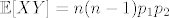 , gdje pripadne slucajne varijable imaju distribuciju koju si naveo. Izracunajmo stoga kovarijancu, dakle dobivamo; , gdje pripadne slucajne varijable imaju distribuciju koju si naveo. Izracunajmo stoga kovarijancu, dakle dobivamo;
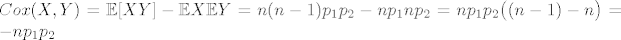
odnosno slijedilo bi da su 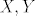 nuzno negativno korelirane, a ne mora biti tako! nuzno negativno korelirane, a ne mora biti tako!
Ispravi me ako grijesim.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
|
| [Vrh] |
|
Froggy
Forumaš(ica)

Pridružen/a: 26. 01. 2012. (23:52:35)
Postovi: (9)16
Spol: 
|
|
| [Vrh] |
|
BlameGame
Forumaš(ica)

Pridružen/a: 14. 09. 2011. (19:17:53)
Postovi: (6C)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
BlameGame
Forumaš(ica)

Pridružen/a: 14. 09. 2011. (19:17:53)
Postovi: (6C)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
 Postano: 1:46 ned, 12. 1. 2014 Naslov: Postano: 1:46 ned, 12. 1. 2014 Naslov: |
    |
|
|
[quote]Mozda netko 5.11 [/quote]
Dakle sjeti se kod definicije fje distribucije da vrijedi
[tex]F_X(x)=\sum\limits_{x \leq y}f_X(y)[/tex]
Sada koristeci to i "viticastu zagradu" odmah slijedi distribucija sl. var. X
P{X=0}=1/4,P{X=1}=1/4,P{X=2}=1/2 (probaj si nacrtati graf ove zadane fje bit ce ti lakse) te od sl. var Y
P{Y=0}=1/4,P{Y=1}=1/4,P{Y=4}=1/2
[b]a)[/b] [tex]P\{0.5 \leq X \leq 1.5\}=P\{X \in [0.5,1.5]\}[/tex] sada se opet sjeti predavanja i da je to zapravo= [tex]\sum\limits_{x \in [0.5,1.5]}f_X(x)=\frac{1}{4}[/tex]
[b]b)[/b] [tex]P\{Y \leq X\}=P\{Y \leq 2\}=\sum\limits_{x \leq 2}f_Y(x)=\frac{1}{2}[/tex]
[b]c)[/b][tex]P\{X+Y \leq 0.75\}=P\{Y \leq 0.75-X\}=P\{Y \leq 0.25\}=\sum\limits_{x \leq 0.25}f_Y(x)=\frac{1}{4}[/tex]
Vidim da je u rjesenjima [tex]\frac{1}{2}[/tex] pa ako netko vidi gdje je greska neka javi. :)
Dakle sjeti se kod definicije fje distribucije da vrijedi
[tex]F_X(x)=\sum\limits_{x \leq y}f_X(y)[/tex]
Sada koristeci to i "viticastu zagradu" odmah slijedi distribucija sl. var. X
P{X=0}=1/4,P{X=1}=1/4,P{X=2}=1/2 (probaj si nacrtati graf ove zadane fje bit ce ti lakse) te od sl. var Y
P{Y=0}=1/4,P{Y=1}=1/4,P{Y=4}=1/2
a) [tex]P\{0.5 \leq X \leq 1.5\}=P\{X \in [0.5,1.5]\}[/tex] sada se opet sjeti predavanja i da je to zapravo= [tex]\sum\limits_{x \in [0.5,1.5]}f_X(x)=\frac{1}{4}[/tex]
b) [tex]P\{Y \leq X\}=P\{Y \leq 2\}=\sum\limits_{x \leq 2}f_Y(x)=\frac{1}{2}[/tex]
c)[tex]P\{X+Y \leq 0.75\}=P\{Y \leq 0.75-X\}=P\{Y \leq 0.25\}=\sum\limits_{x \leq 0.25}f_Y(x)=\frac{1}{4}[/tex]
Vidim da je u rjesenjima [tex]\frac{1}{2}[/tex] pa ako netko vidi gdje je greska neka javi. 
_________________ 
getting recognized |
|
| [Vrh] |
|
|













