| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 12:10 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma Postano: 12:10 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]Iz propozicije o broju surjekcija sa n-clanog u m-clani skup smo za n-ti Bellov broj (broj svih particija n-clanog skupa) dobili:
[latex]\newcommand{\combination}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\newcommand{\largesum}[2]{ \begin{array}{c} \scriptstyle{#2} \\ \sum \\ \scriptstyle{#1} \end{array} }
B_n=\largesum{k=0}{n} \textstyle{\frac{1}{k!}} \largesum{r=0}{k} (-1)^r \combination{m}{r} (m-r)^n =~ ... ~[/latex]
I sada D. Veljan u svojoj knjizi razvija alternativni izraz za n-ti bellov broj na slijedeci nacin (sluzeci se cinjenicom da je izraz unutar sume za k>n jednak 0):
[latex]\newcommand{\combination}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\newcommand{\largesum}[2]{ \begin{array}{c} \scriptstyle{#2} \\ \sum \\ \scriptstyle{#1} \end{array} }
~ ... ~ = \largesum{k=0}{\infty}\frac{1}{k!} \largesum{r=0}{k} (-1)^r \combination{m}{r} (m-r)^n = \\
= \largesum{r=0}{\infty} \frac{r^n}{r!} \largesum{k=r}{\infty} \frac{(-1)^{k-r}}{(k-r)!} = \frac{1}{e} \largesum{r=0}{\infty} \frac{r^n}{r!}[/latex]
Nejasan je samo ovaj lijevi izraz u donjem redu :? Moze li netko pojasniti i/ili uputiti na neki izvor o osnovnom ponasanju beskonacnih suma kod ovakovih rabota ? :?[/quote]
Da, može Sarapa (ne bi čovjek vjerovao: ) - trebalo mu je za neke "trivijalije" u diskretnoj teoriji...
uglavnom, ako dovoljno uporno listaš njegovu knjigu, naći ćeš sve kriterije koji ti mogu u ovakvim situacijama zatrebati.
Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago. :-)
| ZELENIZUBNAPLANETIDOSADE (napisa): | Iz propozicije o broju surjekcija sa n-clanog u m-clani skup smo za n-ti Bellov broj (broj svih particija n-clanog skupa) dobili:
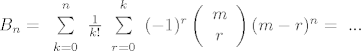
I sada D. Veljan u svojoj knjizi razvija alternativni izraz za n-ti bellov broj na slijedeci nacin (sluzeci se cinjenicom da je izraz unutar sume za k>n jednak 0):
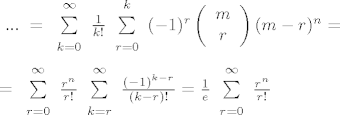
Nejasan je samo ovaj lijevi izraz u donjem redu  Moze li netko pojasniti i/ili uputiti na neki izvor o osnovnom ponasanju beskonacnih suma kod ovakovih rabota ? Moze li netko pojasniti i/ili uputiti na neki izvor o osnovnom ponasanju beskonacnih suma kod ovakovih rabota ?  |
Da, može Sarapa (ne bi čovjek vjerovao: ) - trebalo mu je za neke "trivijalije" u diskretnoj teoriji...
uglavnom, ako dovoljno uporno listaš njegovu knjigu, naći ćeš sve kriterije koji ti mogu u ovakvim situacijama zatrebati.
Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago. 
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 18:40 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma Postano: 18:40 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma |
    |
|
|
[quote="veky"]Da, može Sarapa (ne bi čovjek vjerovao: ) - trebalo mu je za neke "trivijalije" u diskretnoj teoriji...
uglavnom, ako dovoljno uporno listaš njegovu knjigu, naći ćeš sve kriterije koji ti mogu u ovakvim situacijama zatrebati.
Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago. :-)[/quote]
Al nema Sarape knjigu :? no, zadovoljicu se i sa tobom :D znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije? :?
| veky (napisa): | Da, može Sarapa (ne bi čovjek vjerovao: ) - trebalo mu je za neke "trivijalije" u diskretnoj teoriji...
uglavnom, ako dovoljno uporno listaš njegovu knjigu, naći ćeš sve kriterije koji ti mogu u ovakvim situacijama zatrebati.
Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago.  |
Al nema Sarape knjigu  no, zadovoljicu se i sa tobom no, zadovoljicu se i sa tobom  znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije? znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije? 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 19:29 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma Postano: 19:29 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="veky"]Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago. :-)[/quote]
Al nema Sarape knjigu :?[/quote]
Ima knjižnicom.
BTW što je s tvojim padežovima &li glagolskim licima? :-)
[quote] no, zadovoljicu se i sa tobom :D znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije? :?[/quote]
Ako to nešto apsolutno konvergira, i pomnoženo još s ovim ispred njega apsolutno konvergira, da.
| ZELENIZUBNAPLANETIDOSADE (napisa): | | veky (napisa): | Konkretno, ono što ti ovdje treba (bar mislim da se možeš s tim izvući) glasi otprilike: ako red _apsolutno_ konvergira, tad možeš zamjenjivati što ti drago.  |
Al nema Sarape knjigu  |
Ima knjižnicom.
BTW što je s tvojim padežovima &li glagolskim licima? 
| Citat: | no, zadovoljicu se i sa tobom  znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije? znaci... mogu po volji permutirati znakove sumacije i predmete sumiranja dok god postoji nesto iza najdesnijeg znaka sumacije?  |
Ako to nešto apsolutno konvergira, i pomnoženo još s ovim ispred njega apsolutno konvergira, da.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
Gost
|
 Postano: 20:56 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma Postano: 20:56 čet, 9. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma |
    |
|
|
Neka su [latex]a_{i,j}; i,j\in{N}[/latex] elementi od [latex][0,+\infty][/latex] i neka je [latex]\pi\colon{N}\to{N}\times{N}[/latex] bijekcija. Tada vrijedi [latex]\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}a_{i,j}=\sum_{n=1}^{\infty}a_{\pi(n)}=\sum_{j=1}^{\infty}\sum_{i=1}^{\infty}a_{i,j}[/latex].
Pritom su gornje sume elementi od [latex][0,+\infty][/latex], tj. sva tri broja su istovremeno konačna ([latex]\in[0,+\infty\rangle[/latex]) ili beskonačna ([latex]=+\infty[/latex]), i uvijek su jednaki.
Neka su [latex]a_{i,j}; i,j\in{N}[/latex] (realni ili kompleksni) brojevi i neka je [latex]\pi\colon{N}\to{N}\times{N}[/latex] bijekcija.
Iz prethodnog teorema znamo da je [latex]\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}|a_{i,j}|=\sum_{n=1}^{\infty}|a_{\pi(n)}|=
\sum_{j=1}^{\infty}\sum_{i=1}^{\infty}|a_{i,j}|[/latex].
Ukoliko su gornji brojevi konačni ([latex]=+\infty[/latex]), onda vrijedi
[latex]\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}a_{i,j}=\sum_{n=1}^{\infty}a_{\pi(n)}=
\sum_{j=1}^{\infty}\sum_{i=1}^{\infty}a_{i,j}[/latex].
Pritom se tvrdi da svaki od gornjih pet(!) redova (simbolički ih je 5, zapravo ih ima beskonačno) konvergira (zapravo čak apsolutno) i da vrijede gornje jednakosti.
Ukoliko sume nisu po cijelom skupu [latex]{N}[/latex] ili [latex]{N}_0[/latex], npr. [latex]\sum_{i=7}^{\infty}\sum_{j=i^2}^{\infty}a_{i,j}[/latex], onda se dodefinira da preostali [latex]a_{i,j}[/latex]-ovi budu jednaki 0.
Mislim da bi u tvom primjeru trebalo pisati
[quote="ZELENIZUBNAPLANETIDOSADE"][latex]\newcommand{\combination}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\newcommand{\largesum}[2]{ \begin{array}{c} \scriptstyle{#2} \\ \sum \\ \scriptstyle{#1} \end{array} }
~ ... ~ = \largesum{k=0}{\infty}\frac{1}{k!} \largesum{r=0}{k} (-1)^{k-r} \combination{k}{r} r^n
= \largesum{r=0}{\infty} \frac{r^n}{r!} \largesum{k=r}{\infty} \frac{(-1)^{k-r}}{(k-r)!} = \frac{1}{e} \largesum{r=0}{\infty} \frac{r^n}{r!}[/latex][/quote]
Zato za zamjenu redosljeda sumacije treba provjeriti uvjet
[latex]\sum_{r=0}^{\infty}\sum_{k=r}^{\infty}\frac{r^n}{r!(k-r)!}=
e\sum_{r=0}^{\infty}\frac{r^n}{r!}<+\infty[/latex],
a on je doista ispunjen.
Neka su 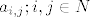 elementi od elementi od 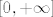 i neka je i neka je 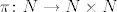 bijekcija. Tada vrijedi bijekcija. Tada vrijedi 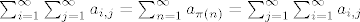 . .
Pritom su gornje sume elementi od 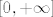 , tj. sva tri broja su istovremeno konačna ( , tj. sva tri broja su istovremeno konačna (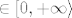 ) ili beskonačna ( ) ili beskonačna (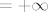 ), i uvijek su jednaki. ), i uvijek su jednaki.
Neka su 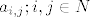 (realni ili kompleksni) brojevi i neka je (realni ili kompleksni) brojevi i neka je 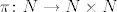 bijekcija. bijekcija.
Iz prethodnog teorema znamo da je 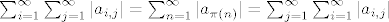 . .
Ukoliko su gornji brojevi konačni (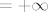 ), onda vrijedi ), onda vrijedi
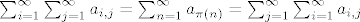 . .
Pritom se tvrdi da svaki od gornjih pet(!) redova (simbolički ih je 5, zapravo ih ima beskonačno) konvergira (zapravo čak apsolutno) i da vrijede gornje jednakosti.
Ukoliko sume nisu po cijelom skupu 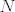 ili ili 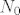 , npr. , npr. 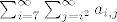 , onda se dodefinira da preostali , onda se dodefinira da preostali 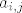 -ovi budu jednaki 0. -ovi budu jednaki 0.
Mislim da bi u tvom primjeru trebalo pisati
| ZELENIZUBNAPLANETIDOSADE (napisa): | 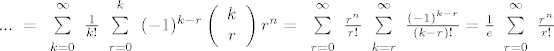 |
Zato za zamjenu redosljeda sumacije treba provjeriti uvjet
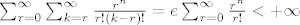 , ,
a on je doista ispunjen.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 13:38 sub, 11. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma Postano: 13:38 sub, 11. 9. 2004 Naslov: Re: Zamjena reda sumacije kod beskonacnih suma |
    |
|
|
[quote="vjekovac"]Sorry, zaboravih se logirati.
Preuzimam odgovornost za gornje tvrdnje i eventualne pogreške.[/quote]
mnogo zahvalan :D
| vjekovac (napisa): | Sorry, zaboravih se logirati.
Preuzimam odgovornost za gornje tvrdnje i eventualne pogreške. |
mnogo zahvalan 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
|





