| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
 Postano: 14:24 pon, 3. 2. 2014 Naslov: Rezultati 2. kolokvija 27.1.2014. Postano: 14:24 pon, 3. 2. 2014 Naslov: Rezultati 2. kolokvija 27.1.2014. |
    |
|
|
U prilogu su rezultati 2. kolokvija iz Vektorskih prostora koji je odrzan 27. sijecnja 2014.
Uvidi za zadatke 2-7 bit ce u utorak 4.2.2014. u 12 sati u predavaonici 006. (T. Pejkovic)
Uvidi za 1. zadatak u utorak 4.2.2014. u 12 sati u uredu prof. Adamovica (2. kat).
[size=9][color=#999999]Added after 27 minutes:[/color][/size]
Mala napomena oko bodovanja. S obzirom da su zadatci bili vrlo vrlo slicni onima u zadnja dva kolokvija koji su vam dostupni na stranici kolegija i s obzirom da ste mogli koristiti kalkulatore, bilo je vrlo bitno dobiti tocan rezultat. Postupak je izuzetno standardan (osim eventualno 7. zad.), pa nema smisla da dobivate bodove zato sto ste npr. znali da trebate izracunati svojstvene vrijednosti ako ih niste tocno izracunali.
Jedini izuzetak koji sam napravio bio je 4. zadatak u kojem je velik broj studenata nazalost odabrao mukotrpni put ortonormiranja baze za W. Mnogi su u tom racunu i uspjeli (posebno ako su izabrali pogodnu bazu).
No, ovakav isti zadatak pojavljuje se u dva prosla kolokvija (i kod njih je dim(W)=3, dim(citavog prostora)=4). Puno je krace odrediti ortonormiranu bazu za ortogonalni komplement od W. S obzirom da je dimenzija tog ortogonalnog komplementa 1, zapravo treba samo normirati dobiveni vektor (koji se moze direktno ocitati iz definicije od W u zadatku). Zatim se od danog vektora (tj. matrice) oduzme projekcija na ortogonalni komplement od W i dobije se ortogonalna projekcija na W, tj. najbolja aproksimacija.
Za ilustraciju. U grupi B se trazila najbolja aproksimacija matrice [latex]A=\begin{pmatrix} 6 & -1 \\ 1 & 1 \end{pmatrix}[/latex] matricama iz potprostora
[latex]W=\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} : 2a+2b-c=0\}.[/latex]
No odavdje direktno ocitavamo da je ortogonalni komplement od W razapet s [latex]\begin{pmatrix} 2 & 2 \\ -1 & 0 \end{pmatrix}[/latex], odnosno nakon normiranja s [latex]u=1/3\begin{pmatrix} 2 & 2 \\ -1 & 0 \end{pmatrix}[/latex]. Sada izracunamo
[latex]A-(A|u)u= \begin{pmatrix} 4 & -3 \\ 2 & 1 \end{pmatrix}[/latex]
u jednom redu i to je to.
U prilogu su rezultati 2. kolokvija iz Vektorskih prostora koji je odrzan 27. sijecnja 2014.
Uvidi za zadatke 2-7 bit ce u utorak 4.2.2014. u 12 sati u predavaonici 006. (T. Pejkovic)
Uvidi za 1. zadatak u utorak 4.2.2014. u 12 sati u uredu prof. Adamovica (2. kat).
Added after 27 minutes:
Mala napomena oko bodovanja. S obzirom da su zadatci bili vrlo vrlo slicni onima u zadnja dva kolokvija koji su vam dostupni na stranici kolegija i s obzirom da ste mogli koristiti kalkulatore, bilo je vrlo bitno dobiti tocan rezultat. Postupak je izuzetno standardan (osim eventualno 7. zad.), pa nema smisla da dobivate bodove zato sto ste npr. znali da trebate izracunati svojstvene vrijednosti ako ih niste tocno izracunali.
Jedini izuzetak koji sam napravio bio je 4. zadatak u kojem je velik broj studenata nazalost odabrao mukotrpni put ortonormiranja baze za W. Mnogi su u tom racunu i uspjeli (posebno ako su izabrali pogodnu bazu).
No, ovakav isti zadatak pojavljuje se u dva prosla kolokvija (i kod njih je dim(W)=3, dim(citavog prostora)=4). Puno je krace odrediti ortonormiranu bazu za ortogonalni komplement od W. S obzirom da je dimenzija tog ortogonalnog komplementa 1, zapravo treba samo normirati dobiveni vektor (koji se moze direktno ocitati iz definicije od W u zadatku). Zatim se od danog vektora (tj. matrice) oduzme projekcija na ortogonalni komplement od W i dobije se ortogonalna projekcija na W, tj. najbolja aproksimacija.
Za ilustraciju. U grupi B se trazila najbolja aproksimacija matrice 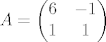 matricama iz potprostora matricama iz potprostora
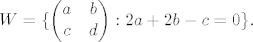
No odavdje direktno ocitavamo da je ortogonalni komplement od W razapet s 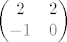 , odnosno nakon normiranja s , odnosno nakon normiranja s 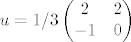 . Sada izracunamo . Sada izracunamo
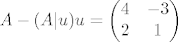
u jednom redu i to je to.
| Description: |
|

Download |
| Filename: |
rez2kol-2013-14.pdf |
| Filesize: |
140.42 KB |
| Downloaded: |
1318 Time(s) |
Zadnja promjena: tp; 15:26 pon, 3. 2. 2014; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
 Postano: 15:30 pon, 3. 2. 2014 Naslov: Postano: 15:30 pon, 3. 2. 2014 Naslov: |
    |
|
|
Uvidi za 1. zadatak u utorak 4.2.2014. u 12 sati u uredu prof. Adamovica (2. kat).
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Anonymous"][quote="tp"]s obzirom da ste mogli koristiti kalkulatore[/quote]
ne znam kako ostali stoje s tim, ali meni je ovo prvi glas o tome...da ne bude zabune, nije da to nešto previše mijenja stvar, ali kalkulator bi bila olakšica[/quote]
Kao sto ste i napisali, ne bi vam previse pomogli, ali svi koji su htjeli, mogli su ih koristiti. Nadam se da vam nije netko rekao da ne smijete koristiti kalkulator.
Uvidi za 1. zadatak u utorak 4.2.2014. u 12 sati u uredu prof. Adamovica (2. kat).
Added after 3 minutes:
| Anonymous (napisa): | | tp (napisa): | | s obzirom da ste mogli koristiti kalkulatore |
ne znam kako ostali stoje s tim, ali meni je ovo prvi glas o tome...da ne bude zabune, nije da to nešto previše mijenja stvar, ali kalkulator bi bila olakšica |
Kao sto ste i napisali, ne bi vam previse pomogli, ali svi koji su htjeli, mogli su ih koristiti. Nadam se da vam nije netko rekao da ne smijete koristiti kalkulator.
|
|
| [Vrh] |
|
četiri
Forumaš(ica)


Pridružen/a: 11. 09. 2012. (20:20:15)
Postovi: (1B)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
iciganov1
Forumaš(ica)
Pridružen/a: 22. 11. 2009. (18:28:55)
Postovi: (7A)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
 Postano: 14:03 uto, 4. 2. 2014 Naslov: Postano: 14:03 uto, 4. 2. 2014 Naslov: |
    |
|
|
U prilogu zadaci i rjesenja (2-7 zad.) 2. kolokvija. Zanemarite brojke 1 ili 2 koje se ponegdje nalaze (u originalu su crvene, ali se to ovdje naravno ne vidi), to je meni samo [i]podsjetnik[/i] na bodovanje.
U prilogu zadaci i rjesenja (2-7 zad.) 2. kolokvija. Zanemarite brojke 1 ili 2 koje se ponegdje nalaze (u originalu su crvene, ali se to ovdje naravno ne vidi), to je meni samo podsjetnik na bodovanje.
| Description: |
|

Download |
| Filename: |
VP-2kol-2013-14-zad_i_rj.pdf |
| Filesize: |
262.38 KB |
| Downloaded: |
1520 Time(s) |
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
merche
Forumaš(ica)

Pridružen/a: 05. 11. 2011. (23:16:10)
Postovi: (3)16
Spol: 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
 Postano: 13:33 pon, 10. 2. 2014 Naslov: Postano: 13:33 pon, 10. 2. 2014 Naslov: |
    |
|
|
[quote="merche"]imam pitanje. zar nije u A grupi u 5. zad. (za V4) norma od (i,0,1)=0 jer je i^2 = -1 ?[/quote]
Ne, skalarni produkt na [tex]\mathbb{C}^n[/tex] definiran je sa [tex](x|y) = \displaystyle \sum_{j=1}^n x_j \cdot \overline{y_j}[/tex]. Tako je [tex]\|(i,0,1)\| = \sqrt{i \cdot (-i) + 0 \cdot 0 + 1 \cdot 1} = 2[/tex].
| merche (napisa): | | imam pitanje. zar nije u A grupi u 5. zad. (za V4) norma od (i,0,1)=0 jer je i^2 = -1 ? |
Ne, skalarni produkt na [tex]\mathbb{C}^n[/tex] definiran je sa [tex](x|y) = \displaystyle \sum_{j=1}^n x_j \cdot \overline{y_j}[/tex]. Tako je [tex]\|(i,0,1)\| = \sqrt{i \cdot (-i) + 0 \cdot 0 + 1 \cdot 1} = 2[/tex].
|
|
| [Vrh] |
|
purist
Forumaš(ica)


Pridružen/a: 20. 09. 2011. (23:16:53)
Postovi: (18)16
Spol: 
|
|
| [Vrh] |
|
merche
Forumaš(ica)

Pridružen/a: 05. 11. 2011. (23:16:10)
Postovi: (3)16
Spol: 
|
|
| [Vrh] |
|
|











