| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 0:08 ned, 12. 9. 2004 Naslov: Littlewood-Offordov problem - vezano na Spernerov teorem Postano: 0:08 ned, 12. 9. 2004 Naslov: Littlewood-Offordov problem - vezano na Spernerov teorem |
    |
|
|
Problem: zadano je n realnih brojeva [latex]a_1, ..., a_n[/latex] t.d. [latex] a_i \ge 1 \forall i[/latex]. Tada izmedju svih 2^n suma oblika [latex]\pm a_1 \pm a_2 \pm ... \pm a_n[/latex], onih kojima je apsolutna vrijednost <1 ima najvise [latex] \left( \begin{array}{c} n \\ ~[~ n/2 ~]~ \end{array} \right)[/latex] (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade :?)
Rijesenje po Veljanu:
Problem mozemo reformulirati ovako: koliko najvise ima vektora [latex](\varepsilon_1, ..., \varepsilon_n)~, ~\varepsilon_i = \pm 1[/latex] t.d. suma [latex]\sum_{i=1}^n \varepsilon_i a_i[/latex] padne u otvoreni interval <-1,1> (ili bilo koji drugi interval duljine 2)?
Uzmimo da sume [latex]a = \sum \varepsilon_i a_i[/latex] i [latex]a` = \sum \varepsilon`_i a_i[/latex] leze u intervalu <-1, 1> i a!=a'. Promotrimo skupove indeksa [latex]J = \{ i \in ~[~n~]~ : \varepsilon_i = 1 \}[/latex] i [latex]J` = \{ i \in ~[~n~]~ : \varepsilon`_i = 1 \}[/latex]. BSO neka je J podskup od J'. Tada je:
[latex]a` - a = \sum \varepsilon_i a_i - \sum \varepsilon`_i a_i = 2 \sum_{i \in J` / J} a_i \ge 2[/latex]
Stoga familija podskupova od J cini antilanac u p.u. skupu B_n (uredjen par partitivnog skupa od [n] i relacije biti podskup), pa iz Spernerovog teorema slijedi tvrdnja.
Pitanje: kako je dosao do one zadnje jednakosti (od 2 sume po indeksima iz J'\J) i kako iz te cinjenice slijedi da je familija podskupova od J antilanac u p.u. skupu B_n
:boliglava: :(
PS Spernerov teorem kaze da je sirina skupa B_n (u smislu iz [url=http://degiorgi.math.hr/forum/viewtopic.php?p=18652#18652]topica o p.u. skupovima i Dilworthovom teoremu[/url]) jednaka [latex] \left( \begin{array}{c} n \\ ~[~ n/2 ~]~ \end{array} \right)[/latex]
Problem: zadano je n realnih brojeva 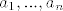 t.d. t.d.  . Tada izmedju svih 2^n suma oblika . Tada izmedju svih 2^n suma oblika 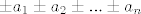 , onih kojima je apsolutna vrijednost <1 ima najvise , onih kojima je apsolutna vrijednost <1 ima najvise 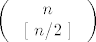 (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade  ) )
Rijesenje po Veljanu:
Problem mozemo reformulirati ovako: koliko najvise ima vektora 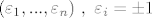 t.d. suma t.d. suma 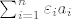 padne u otvoreni interval ←1,1> (ili bilo koji drugi interval duljine 2)? padne u otvoreni interval ←1,1> (ili bilo koji drugi interval duljine 2)?
Uzmimo da sume 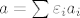 i i 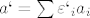 leze u intervalu ←1, 1> i a!=a'. Promotrimo skupove indeksa leze u intervalu ←1, 1> i a!=a'. Promotrimo skupove indeksa 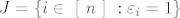 i i 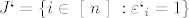 . BSO neka je J podskup od J'. Tada je: . BSO neka je J podskup od J'. Tada je:
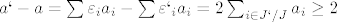
Stoga familija podskupova od J cini antilanac u p.u. skupu B_n (uredjen par partitivnog skupa od [n] i relacije biti podskup), pa iz Spernerovog teorema slijedi tvrdnja.
Pitanje: kako je dosao do one zadnje jednakosti (od 2 sume po indeksima iz J'\J) i kako iz te cinjenice slijedi da je familija podskupova od J antilanac u p.u. skupu B_n
 
PS Spernerov teorem kaze da je sirina skupa B_n (u smislu iz topica o p.u. skupovima i Dilworthovom teoremu) jednaka 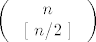
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 1:03 ned, 12. 9. 2004 Naslov: Re: Littlewood-Offordov problem - vezano na Spernerov teorem Postano: 1:03 ned, 12. 9. 2004 Naslov: Re: Littlewood-Offordov problem - vezano na Spernerov teorem |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]Problem: zadano je n realnih brojeva [latex]a_1, ..., a_n[/latex] t.d. [latex] a_i \ge 1 \forall i[/latex]. Tada izmedju svih 2^n suma oblika [latex]\pm a_1 \pm a_2 \pm ... \pm a_n[/latex], onih kojima je apsolutna vrijednost <1 ima najvise [latex] \left( \begin{array}{c} n \\ ~[~ n/2 ~]~ \end{array} \right)[/latex] (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade :?)[/quote]
lfloor i rfloor bi trebali raditi... inFact, [latex]\lfloor\frac{n}{2}\rfloor[/latex]... etoga.
A uvijek možeš napisati i n div 2 :-), ili nešto još bizarnije, poput n>>1 . ;-)
[quote]Rijesenje po Veljanu:
Problem mozemo reformulirati ovako: koliko najvise ima vektora [latex](\varepsilon_1, ..., \varepsilon_n)~, ~\varepsilon_i = \pm 1[/latex] t.d. suma [latex]\sum_{i=1}^n \varepsilon_i a_i[/latex] padne u otvoreni interval <-1,1> (ili bilo koji drugi interval duljine 2)?
Uzmimo da sume [latex]a = \sum \varepsilon_i a_i[/latex] i [latex]a` = \sum \varepsilon`_i a_i[/latex] leze u intervalu <-1, 1> i a!=a'. [/quote]
JC: kad već a crtano vani označavaš kao a' , zašto ne i unutar LaTeX-koda? Ako ništa drugo, uobičajenije je od a` ...
[quote]Promotrimo skupove indeksa [latex]J = \{ i \in ~[~n~]~ : \varepsilon_i = 1 \}[/latex] i [latex]J` = \{ i \in ~[~n~]~ : \varepsilon`_i = 1 \}[/latex]. BSO neka je J podskup od J'. Tada je:
[latex]a` - a = \sum \varepsilon_i a_i - \sum \varepsilon`_i a_i = 2 \sum_{i \in J` / J} a_i \ge 2[/latex][/quote]
U sumama si na krivom mjestu stavio taj svoj famozni ` , al dobro. Jasno je što si htio napisati...
[quote]Stoga familija podskupova od J cini antilanac u p.u. skupu B_n (uredjen par partitivnog skupa od [n] i relacije biti podskup), pa iz Spernerovog teorema slijedi tvrdnja.
Pitanje: kako je dosao do one zadnje jednakosti (od 2 sume po indeksima iz J'\J)[/quote]
Sjeti se, epsovi su brojevi koji su ili 1 ili -1 . Skup [..n] se raspada na 4 podskupa: (1) onaj u kojem su epsovi i eps'ovi jednaki 1 (dakle JnJ' ),
(2) onaj u kojem su epsovi jednaki 1 a eps'ovi jednaki -1 (dakle J\J' ),
(3) onaj u kojem su epsovi jednaki -1 a eps'ovi 1 (dakle J'\J ),
i (4) onaj u kojem su epsovi i eps'ovi jednaki -1 ( (JuJ')^c ).
Ako je J podskup od J' , to zapravo znači da je skup pod [2] prazan. Sumetina po [..n] je tada zbroj sumâ po skupu tipa [1] (što se poništi jer je tamo eps=eps' ), tipa [4] (što se isto poništi, jer je opet eps=eps'(=-1) ), te tipa [3] (to je jedino što ostaje, i tamo je eps'-eps=1-(-1)=2 ).
Dakle, naša sumetina je suma po skupu J'\J , (eps'-eps)a_i , odnosno uzevši u obzir da je eps'-eps=2 , točno ono što nam treba.
[quote] i kako iz te cinjenice slijedi da je familija podskupova od J antilanac u p.u. skupu B_n
:boliglava: :([/quote]
Pa gle... zamisli sve Jove koji odgovaraju takvim sumama (koje su ||<1 ). Gore smo upravo vidjeli da za svaka dva takva (nazvali smo ih maštovitim imenima J i J' ) ne može vrijediti da je JCJ' (jer bi tada razlika njihovih sumâ bila bar 2 , što je poprilično nemoguće ako želimo da obje budu u <-1,1> : ). Sasvim je jasno da je svejedno gdje je crtica, pa isto tako ne može vrijediti ni J'CJ . Dakle, različiti (oni koji nisu jednaki, jel) moraju biti neusporedivi (primijeti da smo sve ostale mogućnosti eliminirali). Dakle, tim sumama u <-1,1> (ili bilo kojem drugom otvorenom intervalu duljine ne vece od 2 ) odgovaraju (injektivno) Jovi koji su medusobno neusporedivi u smislu relacije "biti podskup", odnosno skup svih takvih sumâ ima <= elemenata nego najveći mogući skup neusporedivih Jova u [..n] -- ie, najveći antilanac u [..n] , za kojeg znamo po Sperneru koliko elemenata mora imati.
HTH,
| ZELENIZUBNAPLANETIDOSADE (napisa): | Problem: zadano je n realnih brojeva 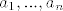 t.d. t.d.  . Tada izmedju svih 2^n suma oblika . Tada izmedju svih 2^n suma oblika 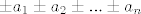 , onih kojima je apsolutna vrijednost <1 ima najvise , onih kojima je apsolutna vrijednost <1 ima najvise 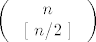 (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade (btw: ne nadjoh znak "najvece cijelo" pa stavio obicne uglate zagrade  ) ) |
lfloor i rfloor bi trebali raditi... inFact, 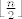 ... etoga. ... etoga.
A uvijek možeš napisati i n div 2  , ili nešto još bizarnije, poput n>>1 . , ili nešto još bizarnije, poput n>>1 . 
| Citat: | Rijesenje po Veljanu:
Problem mozemo reformulirati ovako: koliko najvise ima vektora 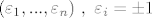 t.d. suma t.d. suma 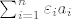 padne u otvoreni interval ←1,1> (ili bilo koji drugi interval duljine 2)? padne u otvoreni interval ←1,1> (ili bilo koji drugi interval duljine 2)?
Uzmimo da sume 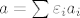 i i 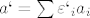 leze u intervalu ←1, 1> i a!=a'. leze u intervalu ←1, 1> i a!=a'. |
JC: kad već a crtano vani označavaš kao a' , zašto ne i unutar LaTeX-koda? Ako ništa drugo, uobičajenije je od a` ...
| Citat: | Promotrimo skupove indeksa 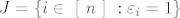 i i 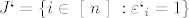 . BSO neka je J podskup od J'. Tada je: . BSO neka je J podskup od J'. Tada je:
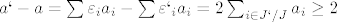 |
U sumama si na krivom mjestu stavio taj svoj famozni ` , al dobro. Jasno je što si htio napisati...
| Citat: | Stoga familija podskupova od J cini antilanac u p.u. skupu B_n (uredjen par partitivnog skupa od [n] i relacije biti podskup), pa iz Spernerovog teorema slijedi tvrdnja.
Pitanje: kako je dosao do one zadnje jednakosti (od 2 sume po indeksima iz J'\J) |
Sjeti se, epsovi su brojevi koji su ili 1 ili -1 . Skup [..n] se raspada na 4 podskupa: (1) onaj u kojem su epsovi i eps'ovi jednaki 1 (dakle JnJ' ),
(2) onaj u kojem su epsovi jednaki 1 a eps'ovi jednaki -1 (dakle J\J' ),
(3) onaj u kojem su epsovi jednaki -1 a eps'ovi 1 (dakle J'\J ),
i (4) onaj u kojem su epsovi i eps'ovi jednaki -1 ( (JuJ')^c ).
Ako je J podskup od J' , to zapravo znači da je skup pod [2] prazan. Sumetina po [..n] je tada zbroj sumâ po skupu tipa [1] (što se poništi jer je tamo eps=eps' ), tipa [4] (što se isto poništi, jer je opet eps=eps'(=-1) ), te tipa [3] (to je jedino što ostaje, i tamo je eps'-eps=1-(-1)=2 ).
Dakle, naša sumetina je suma po skupu J'\J , (eps'-eps)a_i , odnosno uzevši u obzir da je eps'-eps=2 , točno ono što nam treba.
| Citat: | i kako iz te cinjenice slijedi da je familija podskupova od J antilanac u p.u. skupu B_n
  |
Pa gle... zamisli sve Jove koji odgovaraju takvim sumama (koje su ||<1 ). Gore smo upravo vidjeli da za svaka dva takva (nazvali smo ih maštovitim imenima J i J' ) ne može vrijediti da je JCJ' (jer bi tada razlika njihovih sumâ bila bar 2 , što je poprilično nemoguće ako želimo da obje budu u ←1,1> : ). Sasvim je jasno da je svejedno gdje je crtica, pa isto tako ne može vrijediti ni J'CJ . Dakle, različiti (oni koji nisu jednaki, jel) moraju biti neusporedivi (primijeti da smo sve ostale mogućnosti eliminirali). Dakle, tim sumama u ←1,1> (ili bilo kojem drugom otvorenom intervalu duljine ne vece od 2 ) odgovaraju (injektivno) Jovi koji su medusobno neusporedivi u smislu relacije "biti podskup", odnosno skup svih takvih sumâ ima ⇐ elemenata nego najveći mogući skup neusporedivih Jova u [..n] – ie, najveći antilanac u [..n] , za kojeg znamo po Sperneru koliko elemenata mora imati.
HTH,
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 20:44 ned, 12. 9. 2004 Naslov: Postano: 20:44 ned, 12. 9. 2004 Naslov: |
    |
|
|
Thnx veky :) moram to jos raspisat i progruntat ono pa cu mozda imati i jos pokoje pitanje al mitlim da sam svatio :? malo uznemiruje tendencija tog covjeka da se razbacuje rijecima poput "dakle", "poslije kraceg racuna", "lako se izvodi", "nije tesko dokazati", "lako se provjeri", "..prepustamo citatelju" i sl kada naleti na dio dokaza koji je tlaka za raspisati :onfire: :shock:
al dobro, ta e tu e, naprijed u nove radne pobjede :)
Thnx veky  moram to jos raspisat i progruntat ono pa cu mozda imati i jos pokoje pitanje al mitlim da sam svatio moram to jos raspisat i progruntat ono pa cu mozda imati i jos pokoje pitanje al mitlim da sam svatio  malo uznemiruje tendencija tog covjeka da se razbacuje rijecima poput "dakle", "poslije kraceg racuna", "lako se izvodi", "nije tesko dokazati", "lako se provjeri", "..prepustamo citatelju" i sl kada naleti na dio dokaza koji je tlaka za raspisati malo uznemiruje tendencija tog covjeka da se razbacuje rijecima poput "dakle", "poslije kraceg racuna", "lako se izvodi", "nije tesko dokazati", "lako se provjeri", "..prepustamo citatelju" i sl kada naleti na dio dokaza koji je tlaka za raspisati  
al dobro, ta e tu e, naprijed u nove radne pobjede 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 13:13 pon, 13. 9. 2004 Naslov: Postano: 13:13 pon, 13. 9. 2004 Naslov: |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]malo uznemiruje tendencija tog covjeka da se razbacuje rijecima poput "dakle", "poslije kraceg racuna", "lako se izvodi", "nije tesko dokazati", "lako se provjeri", "..prepustamo citatelju" i sl kada naleti na dio dokaza koji je tlaka za raspisati :onfire: :shock:[/quote]
Ehm... ti još nisi polagao modeliranje? ;-X
| ZELENIZUBNAPLANETIDOSADE (napisa): | malo uznemiruje tendencija tog covjeka da se razbacuje rijecima poput "dakle", "poslije kraceg racuna", "lako se izvodi", "nije tesko dokazati", "lako se provjeri", "..prepustamo citatelju" i sl kada naleti na dio dokaza koji je tlaka za raspisati   |
Ehm... ti još nisi polagao modeliranje? ;-X
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 13:39 pon, 13. 9. 2004 Naslov: Postano: 13:39 pon, 13. 9. 2004 Naslov: |
    |
|
|
[quote="veky"]Ehm... ti još nisi polagao modeliranje? ;-X[/quote]
:shock: istina :shock: cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza :blueshock:
| veky (napisa): | | Ehm... ti još nisi polagao modeliranje? ;-X |
 istina istina  cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 14:39 pon, 13. 9. 2004 Naslov: Postano: 14:39 pon, 13. 9. 2004 Naslov: |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="veky"]Ehm... ti još nisi polagao modeliranje? ;-X[/quote]
:shock: istina :shock: cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza :blueshock:[/quote]
hmm :grebgreb: to iz modeliranja or?
ako je, aj mi to lociraj... bas me zanima....
| ZELENIZUBNAPLANETIDOSADE (napisa): | | veky (napisa): | | Ehm... ti još nisi polagao modeliranje? ;-X |
 istina istina  cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza cak je i to bolje od, npr., koristenja velikog slova R (obicnog) za dezigniranje skupa realnih brojeva, slike lin. operatora, ranga operatora, matricnog zapisa tog operatora, sasvim nevinog vektora iz slike i procjene greske i sve u 4 linije istog dokaza  |
hmm  to iz modeliranja or? to iz modeliranja or?
ako je, aj mi to lociraj... bas me zanima....
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 15:19 pon, 13. 9. 2004 Naslov: Postano: 15:19 pon, 13. 9. 2004 Naslov: |
    |
|
|
[quote="Nesi"]hmm :grebgreb: to iz modeliranja or?
ako je, aj mi to lociraj... bas me zanima....[/quote]
When it rains, it pours :roll: izgubio skriptu! :bad-words:
U svakom slucaju, negdje oko elektricnih mreza, poglavlje prije ili kasnije :? Na pocetku strane (tj. "dokaz" brejka sa prethodne strane i vecina ga je na iducoj - nazalost ne pamtim i o cemu se tocno radilo :?)
| Nesi (napisa): | hmm  to iz modeliranja or? to iz modeliranja or?
ako je, aj mi to lociraj... bas me zanima.... |
When it rains, it pours  izgubio skriptu! izgubio skriptu! 
U svakom slucaju, negdje oko elektricnih mreza, poglavlje prije ili kasnije  Na pocetku strane (tj. "dokaz" brejka sa prethodne strane i vecina ga je na iducoj - nazalost ne pamtim i o cemu se tocno radilo Na pocetku strane (tj. "dokaz" brejka sa prethodne strane i vecina ga je na iducoj - nazalost ne pamtim i o cemu se tocno radilo  ) )
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
|






