Sve je moguce

[osvetnik]

Oprostit cete mi na zahrdjalosti, ali zanima me kako matematicki napisati izraz "Sve je moguce" tj. da je vjerojatnost dogadjaja >0, s tim da je taj dogadjaj element skupa svim mogucih dogadjaja.

P({w})>0
w e S

Da li bi to bilo ok?

[krcko]

Neka je (S,F,P) vjerojatnosni prostor (obično se umjesto S koristi 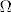). Elemente skupa S zovemo elementarni događaji, elemente sigma algebre F događaji (to su podskupovi od S), a P je vjerojatnost. Ako P(A)>0 čitaš "događaj A je moguć", napisao si da je svaki elementarni događaj moguć. To ipak ne vrijedi za sve događaje jer je po definiciji prazan skup događaj, a njegova vjerojatnost je nula.

Dakle nije sve moguće.

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[Phoenix]

Ova interpretacija na prvu izgleda ispravna, no čini mi se da nije dobra. Primjerice, vjerojatnost da iz skupa [tex]\left[ 0,1 \right][/tex] izaberem broj [tex]\frac{1}{2}[/tex], po neprekidnoj uniformnoj distribuciji na tom skupu, je nula. Međutim, moguće je da izaberem taj broj! Štoviše, vjerojatnost je nula koji god broj da odaberem, no ako se od mene traži da odaberem neki broj, odabrat ću ga - dakle, sigurno će se dogoditi događaj koji je vjerojatnosti nula!

Moje poimanje bi bilo da je to svaki događaj [tex]A \neq \emptyset[/tex]. Primjerice, moguće je da s bacanjem simetričnog novčića beskonačno mnogo puta konstantno dobivam glavu; to bi bio događaj [tex]\left\{ GGGGGGGG \dots \right\}[/tex]. Međutim, nije moguće da u prvom bacanju dobijem i glavu i pismo; to je onda događaj [tex] \left\{ a_1a_2a_3 \dots : a_1 = G \wedge a_1 = P, a_i \in \left\{ G, P \right\}, i \geq 2 \right\} = \emptyset [/tex].
I nije neka zanimljiva interpretacija obzirom da smo izbjegli spomen vjerojatnosti i da smo samo ostali na skupovima.

Ovim se nadovezujem na krcka, ali shvaćam i prvotnu ideju, nešto u stilu "sve što ima smisla/logično je, moguće je" (namjerno ću ostati na ovoj nepreciznoj izjavi da ne bih upao u filozofsku raspravu).

_________________
Mario Stipčić

[osvetnik]

samo da razjasnim, jasno mi je da je izjava iza izraza kriva samo me zanimalo da li sam matematički ispravno napisao ono sto sam htio reci

[krcko]

[osvetnik]

[Phoenix]