| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 1:39 sri, 8. 12. 2004 Naslov: Podsjetnik Postano: 1:39 sri, 8. 12. 2004 Naslov: Podsjetnik |
    |
|
|
Evo, da ne budem bas skroz lijen... Poceo sam sastavljati podsjetnik za MA1.
Pisem ga u LaTeX-u i tu i tamo koristim ruzne hackove i apsolutno ga kozmeticki ne uljepsavam, pa molim da ne gledate kod ako bas ne morate i ne rugate se mom nenamjernom neznanju. :oops:
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
2. nabubetati sve definicije k'o vodu pit'
3. dokazati prvi teorem/propoziciju pomocu nabubetanih aksioma/definicija
4. kad je teorem/propozicija shvacen/a, nabubetati ga/ju k'o vodu pit' kako bi posluzio pri dokazu iducih teorema/propozicija
5. zapisati glavnu ideju pri dokazivanju teorema u obliku algoritma na vidljivo mjesto
6. ponavljati 3., 4. i 5. dok se biljeske ne iscrpe
Naravno, treba se u radu osloniti i udzbenike te prema potrebi ici na konzultacije, demonstrature itd., cisto da me netko ne zgrabi kasnije za siju i priupita: "A zakej one tvoje biljeske ne pale?". :D
BKB, podsjetnik mozete naci na:
http://free-zg.htnet.hr/gurps/ma.pdf
Druge formate ([b]dostupne[/b] na istom mjestu) zelite (valjda) ako i samo ako biste razumjeli sto bih bio zelio reci da sam u URL-u napisao ma.{pdf,dvi,tex}. :twisted:
Odmah se ogradujem od svih mogucix texnickix, ortografijskix, sintaktickix, leksickix, semantickix i eventualnih inix pogresaka jer sam umoran k'o pasce poslije igre omiljenom gumenom igrackom i volio bih zato u vama inducirati odredenu dozu empatije, ali i osjecaj duznosti da mi greske (i/ili nepotpunosti) prijavite. :shock:
Verzija je 0.0.1. To bi trebalo ukazati na cinjenicu da namjeravam prosiriti podsjetnik novim aksiomima/definicijama i da cu nastojati dodati sve teoreme/propozicije koje smo dokazali na predavanjima uz, kao sto ranije rekoh, kratak postupak za samostalan uspjeh u njihovom raspetljavanju.
Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna. 8)
[color=darkred][b]Admin edit:[/b] Iskreno, ne da mi se citati taj PDF, ali djeluje korisno, pa "unaprijedjih" topic u "[i]sticky[/i]".[/color] :D
[color=blue][b]Smith edit:[/b][/color] Hvala na ljepljivosti! :D
Evo, da ne budem bas skroz lijen... Poceo sam sastavljati podsjetnik za MA1.
Pisem ga u LaTeX-u i tu i tamo koristim ruzne hackove i apsolutno ga kozmeticki ne uljepsavam, pa molim da ne gledate kod ako bas ne morate i ne rugate se mom nenamjernom neznanju. 
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
2. nabubetati sve definicije k'o vodu pit'
3. dokazati prvi teorem/propoziciju pomocu nabubetanih aksioma/definicija
4. kad je teorem/propozicija shvacen/a, nabubetati ga/ju k'o vodu pit' kako bi posluzio pri dokazu iducih teorema/propozicija
5. zapisati glavnu ideju pri dokazivanju teorema u obliku algoritma na vidljivo mjesto
6. ponavljati 3., 4. i 5. dok se biljeske ne iscrpe
Naravno, treba se u radu osloniti i udzbenike te prema potrebi ici na konzultacije, demonstrature itd., cisto da me netko ne zgrabi kasnije za siju i priupita: "A zakej one tvoje biljeske ne pale?". 
BKB, podsjetnik mozete naci na:
http://free-zg.htnet.hr/gurps/ma.pdf
Druge formate (dostupne na istom mjestu) zelite (valjda) ako i samo ako biste razumjeli sto bih bio zelio reci da sam u URL-u napisao ma.{pdf,dvi,tex}. 
Odmah se ogradujem od svih mogucix texnickix, ortografijskix, sintaktickix, leksickix, semantickix i eventualnih inix pogresaka jer sam umoran k'o pasce poslije igre omiljenom gumenom igrackom i volio bih zato u vama inducirati odredenu dozu empatije, ali i osjecaj duznosti da mi greske (i/ili nepotpunosti) prijavite. 
Verzija je 0.0.1. To bi trebalo ukazati na cinjenicu da namjeravam prosiriti podsjetnik novim aksiomima/definicijama i da cu nastojati dodati sve teoreme/propozicije koje smo dokazali na predavanjima uz, kao sto ranije rekoh, kratak postupak za samostalan uspjeh u njihovom raspetljavanju.
Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna. 
Admin edit: Iskreno, ne da mi se citati taj PDF, ali djeluje korisno, pa "unaprijedjih" topic u "sticky". 
Smith edit: Hvala na ljepljivosti! 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 16:45 čet, 9. 12. 2004 Naslov: Re: Podsjetnik Postano: 16:45 čet, 9. 12. 2004 Naslov: Re: Podsjetnik |
    |
|
|
[quote="Smith"]
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
[/quote]
C'mon... "nabubetati ko vodu pit" moglo bi odbiti neke ljude. :-o Da, znam da _ti_ ne misliš time ništa loše, ali...
Npr. aksiomi realnih brojeva. Puno se bolje "nabubetaju" ako čovjek prethodno pročita (ili napiše; ) nešto poput http://web.math.hr/~veky/hsmath/L2/polje.html . :-)
[quote]Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna. 8)[/quote]
Ukratko, I'm impressed. :!:
Samo jednu grešku nađoh, i to zato što nisi backslashirao vitičaste zagrade u definiciji domene razlomljene linearne funkcije. :-)
Ako ovakvim entuzijazmom nastaviš, ništa te neće zaustaviti. ;-)
| Smith (napisa): |
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
|
C'mon... "nabubetati ko vodu pit" moglo bi odbiti neke ljude.  Da, znam da _ti_ ne misliš time ništa loše, ali... Da, znam da _ti_ ne misliš time ništa loše, ali...
Npr. aksiomi realnih brojeva. Puno se bolje "nabubetaju" ako čovjek prethodno pročita (ili napiše; ) nešto poput http://web.math.hr/~veky/hsmath/L2/polje.html . 
| Citat: | Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna.  |
Ukratko, I'm impressed. 
Samo jednu grešku nađoh, i to zato što nisi backslashirao vitičaste zagrade u definiciji domene razlomljene linearne funkcije. 
Ako ovakvim entuzijazmom nastaviš, ništa te neće zaustaviti. 
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 19:10 čet, 9. 12. 2004 Naslov: Re: Podsjetnik Postano: 19:10 čet, 9. 12. 2004 Naslov: Re: Podsjetnik |
    |
|
|
[quote="veky"][quote="Smith"]
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
[/quote]
C'mon... "nabubetati ko vodu pit" moglo bi odbiti neke ljude. :-o Da, znam da _ti_ ne misliš time ništa loše, ali...[/quote]
Mm-hm, u pravu si...
[quote="Veky"]Npr. aksiomi realnih brojeva. Puno se bolje "nabubetaju" ako čovjek prethodno pročita (ili napiše; ) nešto poput http://web.math.hr/~veky/hsmath/L2/polje.html . :-)[/quote]
Vec jesam. :wink:
(Slinio sam nad onim nulama, remember? :D)
[quote="Veky"][quote]Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna. 8)[/quote]
Ukratko, I'm impressed. :!:[/quote]
Wow... Thanx! 8)
[quote="Veky"]
Samo jednu grešku nađoh, i to zato što nisi backslashirao vitičaste zagrade u definiciji domene razlomljene linearne funkcije. :-)[/quote]
Hmmm... Ne kuzim. Zapis domene RLF ne sadrzi nikakve viticaste zagrade.
[quote="Veky"]Ako ovakvim entuzijazmom nastaviš, ništa te neće zaustaviti. ;-)[/quote]
Heh', hvala na dovoljnom (jasno, ne i nuznom! :wink:) podstr(j)eku za nastavak rada! :D
| veky (napisa): | | Smith (napisa): |
Pisem ga na nacin da omoguci tip ucenja koji ja smatram jedinim prihvatljivim:
1. nabubetati sve aksiome k'o vodu pit'
|
C'mon... "nabubetati ko vodu pit" moglo bi odbiti neke ljude.  Da, znam da _ti_ ne misliš time ništa loše, ali... Da, znam da _ti_ ne misliš time ništa loše, ali... |
Mm-hm, u pravu si...
Vec jesam. 
(Slinio sam nad onim nulama, remember?  ) )
| Veky (napisa): | | Citat: | Svaka povratna informacija bilo tu u obliku post-a, na PM ili mail-om je pozeljna.  |
Ukratko, I'm impressed.  |
Wow... Thanx! 
| Veky (napisa): |
Samo jednu grešku nađoh, i to zato što nisi backslashirao vitičaste zagrade u definiciji domene razlomljene linearne funkcije.  |
Hmmm... Ne kuzim. Zapis domene RLF ne sadrzi nikakve viticaste zagrade.
| Veky (napisa): | Ako ovakvim entuzijazmom nastaviš, ništa te neće zaustaviti.  |
Heh', hvala na dovoljnom (jasno, ne i nuznom!  ) podstr(j)eku za nastavak rada! ) podstr(j)eku za nastavak rada! 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 20:25 pet, 10. 12. 2004 Naslov: Postano: 20:25 pet, 10. 12. 2004 Naslov: |
    |
|
|
[color=blue][b]Prva revizija![/b][/color]
Napravio sam neke dorade u podsjetniku i odlucio ga baciti na svoj web kao prvu reviziju. 8)
Trenutna verzija je stoga [color=blue][b]0.0.1-r1[/b][/color].
[color=blue][b]Changelog (0.0.1 -> 0.0.1-r1)[/b]
[list][*]dodane [i]steaming hot[/i] definicije
[*]dodano prvih nekoliko teorema
[*]ispravljene krupnije tipografske gr(j)eske
[*]veca dosljednost oznaka u definicijama[/list:u][/color]
Nastojat cu pojednostaviti neke dokaze koje smo radili uvodenjem prirodnijih oznaka (npr. Teorem 1.5. i Teorem 1.6.), dodavanjem nekih nedorecenosti (npr. Teorem 1.5.) i, rjede, sazimanjem gdje je to moguce (npr. Teorem 1.3.).
Kasnije planiram uvesti, kako sam i najavio, recenicu-dvije pri pocetku svakog dokaza koje daju hint-ove kako izvesti dokaz. To, IMHO, olaksava vjezbu pri samostalnom radu.
Trebat ce mi jos dosta vremena da pretipkam sve te teoreme (okvirno, zasad ih ima jos 20 and they keep on coming!). Zato molim za strpljenje. :wink:
(Bas bi netko osim Vekyja mogao barem iskritizirati podsjetnik ako mi vec ne kani prijaviti pogr(j)eske! :evil:)
Prva revizija!
Napravio sam neke dorade u podsjetniku i odlucio ga baciti na svoj web kao prvu reviziju. 
Trenutna verzija je stoga 0.0.1-r1.
Changelog (0.0.1 -> 0.0.1-r1)
- dodane steaming hot definicije
- dodano prvih nekoliko teorema
- ispravljene krupnije tipografske gr(j)eske
- veca dosljednost oznaka u definicijama
Nastojat cu pojednostaviti neke dokaze koje smo radili uvodenjem prirodnijih oznaka (npr. Teorem 1.5. i Teorem 1.6.), dodavanjem nekih nedorecenosti (npr. Teorem 1.5.) i, rjede, sazimanjem gdje je to moguce (npr. Teorem 1.3.).
Kasnije planiram uvesti, kako sam i najavio, recenicu-dvije pri pocetku svakog dokaza koje daju hint-ove kako izvesti dokaz. To, IMHO, olaksava vjezbu pri samostalnom radu.
Trebat ce mi jos dosta vremena da pretipkam sve te teoreme (okvirno, zasad ih ima jos 20 and they keep on coming!). Zato molim za strpljenje. 
(Bas bi netko osim Vekyja mogao barem iskritizirati podsjetnik ako mi vec ne kani prijaviti pogr(j)eske!  ) )
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
Zadnja promjena: Smith; 21:19 pet, 10. 12. 2004; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 21:10 pet, 10. 12. 2004 Naslov: Postano: 21:10 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote="veky"][quote="HijenA"]:-k interesantno da se nitko prije tebe nije sjetio napraviti slican podsjetnik :?[/quote]
Jest, ali za internu upotrebu.
Nemamo svi toliko entuzijazma usklađivati svoju privatnu notaciju s onim što bi većina ljudi očekivala. Smithu svaka čast, baš me zanima koliko dugo će izdržati... ;-)[/quote]
ne kuzim...ako netko napravi kompilaciju onoga sto se uci, ali krace zapisano, kako se to kosi sa notacijom vecine? osim toga, matematicki pojmovi su standardizirani (nemoj razvijat diskusiju o ovome pojmu :) ) i tu nema govora o privatnoj ili bilo kakvoj drugoj notaciji. stvar je samo u prikazu.
| veky (napisa): | | HijenA (napisa): |  interesantno da se nitko prije tebe nije sjetio napraviti slican podsjetnik interesantno da se nitko prije tebe nije sjetio napraviti slican podsjetnik  |
Jest, ali za internu upotrebu.
Nemamo svi toliko entuzijazma usklađivati svoju privatnu notaciju s onim što bi većina ljudi očekivala. Smithu svaka čast, baš me zanima koliko dugo će izdržati...  |
ne kuzim...ako netko napravi kompilaciju onoga sto se uci, ali krace zapisano, kako se to kosi sa notacijom vecine? osim toga, matematicki pojmovi su standardizirani (nemoj razvijat diskusiju o ovome pojmu  ) i tu nema govora o privatnoj ili bilo kakvoj drugoj notaciji. stvar je samo u prikazu. ) i tu nema govora o privatnoj ili bilo kakvoj drugoj notaciji. stvar je samo u prikazu.
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 21:13 pet, 10. 12. 2004 Naslov: Postano: 21:13 pet, 10. 12. 2004 Naslov: |
    |
|
|
Nisam pecao komplimente, ali uvijek gode. Hvala, decki! :wink:
Bez brige, HijenA - kao sto vidis, trudim se prosirivati ga. Kazem, ima toga puno, samo je pitanje vremena kad cu sve uvrstiti... Moglo bi potrajati. :roll:
Kad je Veky spomenuo privatnu notaciju, mislio je na oznake koje ja u svojim biljeznicama koristim kako bih skratio potrebno vrijeme za zapisivanje neceg i za kasnije lakse razumijevanje napisanog. Recimo, meni je lakse napisati "a||b" (gdje su || dvije vertikalne str(j)elice prema gore) nego "a je kolinearno s b", a i kasnije to procitati i razumjeti. Stvar je prilicno individualna i mnogi se sa mnom ne bi slozili.
Sto se samog podsjetnika tice, napravili su ljudi slicnu stvar vec, npr. kolega Cinik je sastavio texnicki zadivljujuce rijesene biljeske :shock:, ali za drugu godinu.
Veky, nije mi problem transkribirati dokaze jer u dokazima nemam razloga koristiti previse vlastite notacije.
To mi ponajvise koristi u zadacima (barem je tako u MA) - na vjezbama vise volim eksperimentirati.
Jedan od razloga za to je, primjerice, fantasticna sistematicnost prof. Bakica iz LA koju se bojim narusavati svojim oznakama (zbog povremenih jezicnih bravura u dokazima koje ne mogu oslikati oznakicama, a uvelike pomazu u razumijevanju).
BKB, dozivjet ce moj podsjetnik jos puuuno novih verzija! 8)
Nisam pecao komplimente, ali uvijek gode. Hvala, decki! 
Bez brige, HijenA - kao sto vidis, trudim se prosirivati ga. Kazem, ima toga puno, samo je pitanje vremena kad cu sve uvrstiti... Moglo bi potrajati. 
Kad je Veky spomenuo privatnu notaciju, mislio je na oznake koje ja u svojim biljeznicama koristim kako bih skratio potrebno vrijeme za zapisivanje neceg i za kasnije lakse razumijevanje napisanog. Recimo, meni je lakse napisati "a||b" (gdje su || dvije vertikalne str(j)elice prema gore) nego "a je kolinearno s b", a i kasnije to procitati i razumjeti. Stvar je prilicno individualna i mnogi se sa mnom ne bi slozili.
Sto se samog podsjetnika tice, napravili su ljudi slicnu stvar vec, npr. kolega Cinik je sastavio texnicki zadivljujuce rijesene biljeske  , ali za drugu godinu. , ali za drugu godinu.
Veky, nije mi problem transkribirati dokaze jer u dokazima nemam razloga koristiti previse vlastite notacije.
To mi ponajvise koristi u zadacima (barem je tako u MA) - na vjezbama vise volim eksperimentirati.
Jedan od razloga za to je, primjerice, fantasticna sistematicnost prof. Bakica iz LA koju se bojim narusavati svojim oznakama (zbog povremenih jezicnih bravura u dokazima koje ne mogu oslikati oznakicama, a uvelike pomazu u razumijevanju).
BKB, dozivjet ce moj podsjetnik jos puuuno novih verzija! 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:41 pet, 10. 12. 2004 Naslov: Postano: 21:41 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote="Smith"]Nisam pecao komplimente,[/quote]
Ok then... :->
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi.
Limes inferior: ista stvar, mutatis mutandis, i pored toga, crta ne samo da ne ide skroz ispod a_n , nego ide iznad n - dakle, kao podvučen lim .
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}->|R _ili_ f:I->|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... :roll:
Teorem 1.2: Please, koristi oble zagrade za sve primjene funkcije na argumente, i za grupiranje. Puno standardnije je that way. Uglate i vitičaste zagrade su definitivno overloaded u današnjoj simbolici...
(Ista stvar i u dokazu dovoljnosti u T1.3)
| Smith (napisa): | | Nisam pecao komplimente, |
Ok then... :→
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi.
Limes inferior: ista stvar, mutatis mutandis, i pored toga, crta ne samo da ne ide skroz ispod a_n , nego ide iznad n - dakle, kao podvučen lim .
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}→|R _ili_ f:I→|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... 
Teorem 1.2: Please, koristi oble zagrade za sve primjene funkcije na argumente, i za grupiranje. Puno standardnije je that way. Uglate i vitičaste zagrade su definitivno overloaded u današnjoj simbolici...
(Ista stvar i u dokazu dovoljnosti u T1.3)
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 22:40 pet, 10. 12. 2004 Naslov: Postano: 22:40 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi.[/quote]
Cekaj... Nije li maksimum skupa A upravo limes superior niza?
Zasad sam samo maknuo to "maksimum" i "minimum", pa cu uvrstiti ono sto je tocno kad razrijesimo omanje nesigurnosti u mom shvacanju ovoga. :D
[quote="veky"]
Limes inferior: ista stvar, mutatis mutandis, i pored toga, crta ne samo da ne ide skroz ispod a_n , nego ide iznad n - dakle, kao podvučen lim .
[/quote]
Hehe, rijeseno. Sad sam tek otkrio da postoje \varlimsup i \varliminf. :D
[quote="veky"]
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}->|R _ili_ f:I->|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
[/quote]
Provjeri je li sad OK. Inace, definicija je oridjidji ona kako smo ju zapisali na predavanju...
[quote="veky"]
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... :roll:
[/quote]
Da, slazem se... Razmisljao sam da to izbacim.
Naime, prof. Guljas je uvrstio taj dio u dokaz jer je vjerojatno smatrao da je treci red pretjerano dug za odjednom parsati.
Uglavnom, 4. i 5. red su sad bivsi. 8)
[quote="veky"]
Teorem 1.2: Please, koristi oble zagrade za sve primjene funkcije na argumente, i za grupiranje. Puno standardnije je that way. Uglate i vitičaste zagrade su definitivno overloaded u današnjoj simbolici...[/quote]
Jos jednom, slazem se, ali tako smo to bili zapisali na nastavi iskljucivo da bi se vidjelo kojim redom se sto radi.
Popravljeno. :wink:
[quote="veky"]
(Ista stvar i u dokazu dovoljnosti u T1.3)[/quote]
Ditto. :D
| veky (napisa): |
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi. |
Cekaj... Nije li maksimum skupa A upravo limes superior niza?
Zasad sam samo maknuo to "maksimum" i "minimum", pa cu uvrstiti ono sto je tocno kad razrijesimo omanje nesigurnosti u mom shvacanju ovoga. 
| veky (napisa): |
Limes inferior: ista stvar, mutatis mutandis, i pored toga, crta ne samo da ne ide skroz ispod a_n , nego ide iznad n - dakle, kao podvučen lim .
|
Hehe, rijeseno. Sad sam tek otkrio da postoje \varlimsup i \varliminf. 
| veky (napisa): |
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}->|R _ili_ f:I->|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
|
Provjeri je li sad OK. Inace, definicija je oridjidji ona kako smo ju zapisali na predavanju...
| veky (napisa): |
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... 
|
Da, slazem se... Razmisljao sam da to izbacim.
Naime, prof. Guljas je uvrstio taj dio u dokaz jer je vjerojatno smatrao da je treci red pretjerano dug za odjednom parsati.
Uglavnom, 4. i 5. red su sad bivsi. 
| veky (napisa): |
Teorem 1.2: Please, koristi oble zagrade za sve primjene funkcije na argumente, i za grupiranje. Puno standardnije je that way. Uglate i vitičaste zagrade su definitivno overloaded u današnjoj simbolici... |
Jos jednom, slazem se, ali tako smo to bili zapisali na nastavi iskljucivo da bi se vidjelo kojim redom se sto radi.
Popravljeno. 
| veky (napisa): |
(Ista stvar i u dokazu dovoljnosti u T1.3) |
Ditto. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 23:25 pet, 10. 12. 2004 Naslov: Postano: 23:25 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote="Smith"][quote="veky"]
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi.[/quote]
Cekaj... Nije li maksimum skupa A upravo limes superior niza?[/quote]
Jest. No pisalo je "... i zovemo ga limes superior (najveće gomilište, maksimum) tog niza." Primijeti, nigdje ne piše "maksimum skupa A ". Piše "maksimum (tog niza)" kao zamjena za "limsup (tog niza)". You see?
[quote]Zasad sam samo maknuo to "maksimum" i "minimum", pa cu uvrstiti ono sto je tocno kad razrijesimo omanje nesigurnosti u mom shvacanju ovoga. :D[/quote]
Ma napiši što hoćeš, neće ti to nitko ocjenjivati. ;-) Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-...
[quote][quote="veky"]
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}->|R _ili_ f:I->|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
[/quote]
Provjeri je li sad OK. Inace, definicija je oridjidji ona kako smo ju zapisali na predavanju...[/quote]
Sad mi se više sviđa. Prof.Guljašu vjerojatno f: D->K prije znači nešto u smislu " f je definirana na D sigurno, ali može biti i drugdje"... i tako se često promatraju stvari u analizi. No bar u početku bilo bi dobro striktno se držati definicijâ. A reći da sinus nije neprekidan u 0 samo zato što mu domena nije oblika I\.{0} je prilično silly. :-)
[quote][quote="veky"]
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... :roll:
[/quote]
Da, slazem se... Razmisljao sam da to izbacim.
Naime, prof. Guljas je uvrstio taj dio u dokaz jer je vjerojatno smatrao da je treci red pretjerano dug za odjednom parsati.[/quote]
:?: Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza. Ili bar napiši: "uz eps:=|x|+|y| (ili što već), ..."
[quote]Uglavnom, 4. i 5. red su sad bivsi. 8)[/quote]
:amen: :-)
[quote]Jos jednom, slazem se, ali tako smo to bili zapisali na nastavi iskljucivo da bi se vidjelo kojim redom se sto radi.[/quote]
Whatever. Tome i služe zagrade, no ne moraju zato biti raznih oblikâ. ;-o
| Smith (napisa): | | veky (napisa): |
Limes superior: gornja crta ide samo nad lim, ne nad a_n . Limes superior niza a možeš "zvati" najveće gomilište niza a jer on to zaista jest (pokazuje se da skup A uvijek ima maksimum), ali ne možeš ga zvati maksimum niza a općenito, kao što bi nepažljiv čitatelj mogao zaključiti iz onog što piše u zagradi. |
Cekaj... Nije li maksimum skupa A upravo limes superior niza? |
Jest. No pisalo je "... i zovemo ga limes superior (najveće gomilište, maksimum) tog niza." Primijeti, nigdje ne piše "maksimum skupa A ". Piše "maksimum (tog niza)" kao zamjena za "limsup (tog niza)". You see?
| Citat: | Zasad sam samo maknuo to "maksimum" i "minimum", pa cu uvrstiti ono sto je tocno kad razrijesimo omanje nesigurnosti u mom shvacanju ovoga.  |
Ma napiši što hoćeš, neće ti to nitko ocjenjivati.  Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-... Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-...
| Citat: | | veky (napisa): |
Limes funkcije u točki: zgodna definicija, ali baš ne all-encompassing onog što ti treba. Ipak bi bilo bolje reći f:I\.{c}→|R _ili_ f:I→|R . Često se pitaš kakvi su limesi funkcijâ koje su već definirane u toj točki.
|
Provjeri je li sad OK. Inace, definicija je oridjidji ona kako smo ju zapisali na predavanju... |
Sad mi se više sviđa. Prof.Guljašu vjerojatno f: D→K prije znači nešto u smislu " f je definirana na D sigurno, ali može biti i drugdje"... i tako se često promatraju stvari u analizi. No bar u početku bilo bi dobro striktno se držati definicijâ. A reći da sinus nije neprekidan u 0 samo zato što mu domena nije oblika I\.{0} je prilično silly. 
| Citat: | | veky (napisa): |
Propozicija 1.1: Otkud epsilon tu zalutao?? 4. i 5. red dokaza su totalno suvišni, kao da su iz nekog drugog crtića... 
|
Da, slazem se... Razmisljao sam da to izbacim.
Naime, prof. Guljas je uvrstio taj dio u dokaz jer je vjerojatno smatrao da je treci red pretjerano dug za odjednom parsati. |
 Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza. Ili bar napiši: "uz eps:=|x|+|y| (ili što već), ..." Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza. Ili bar napiši: "uz eps:=|x|+|y| (ili što već), ..."
| Citat: | Uglavnom, 4. i 5. red su sad bivsi.  |
 
| Citat: | | Jos jednom, slazem se, ali tako smo to bili zapisali na nastavi iskljucivo da bi se vidjelo kojim redom se sto radi. |
Whatever. Tome i služe zagrade, no ne moraju zato biti raznih oblikâ. ;-o
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 0:12 sub, 11. 12. 2004 Naslov: Postano: 0:12 sub, 11. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]Primijeti, nigdje ne piše "maksimum skupa A ". Piše "maksimum (tog niza)" kao zamjena za "limsup (tog niza)". You see?[/quote]
Sredih. 8)
[quote="veky"]Ma napiši što hoćeš, neće ti to nitko ocjenjivati. ;-) Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-...[/quote]
Kvac'ca. :wink:
[quote="veky"]
Prof.Guljašu vjerojatno f: D->K prije znači nešto u smislu " f je definirana na D sigurno, ali može biti i drugdje"... i tako se često promatraju stvari u analizi. No bar u početku bilo bi dobro striktno se držati definicijâ. A reći da sinus nije neprekidan u 0 samo zato što mu domena nije oblika I\.{0} je prilično silly. :-)[/quote]
Op't kvac'ca. :wink: :wink:
[quote="veky"]
:?: Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza.[/quote]
To je bila i namjera, samo sto to nisam istaknuo jer ne volim boldati simboliku, a nije mi se dalo sad to ici zaokruzivati ili neke slicne perverzije raditi. :twisted:
[quote="veky"]Ili bar napiši: "uz eps:=|x|+|y| (ili što već), ..."[/quote]
Ma nije bitno. Pusti epsilon da pociva u miru. :D
[quote="veky"]
:amen: :-)[/quote]
Aleluja! :)
[quote="veky"]
Tome i služe zagrade, no ne moraju zato biti raznih oblikâ. ;-o[/quote]
Hehe, okej. :lol:
| veky (napisa): | | Primijeti, nigdje ne piše "maksimum skupa A ". Piše "maksimum (tog niza)" kao zamjena za "limsup (tog niza)". You see? |
Sredih. 
| veky (napisa): | Ma napiši što hoćeš, neće ti to nitko ocjenjivati.  Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-... Ja ti samo primjećujem gdje bi ponetko mogao ponešto krivo shvatiti. :-... |
Kvac'ca. 
| veky (napisa): |
Prof.Guljašu vjerojatno f: D->K prije znači nešto u smislu " f je definirana na D sigurno, ali može biti i drugdje"... i tako se često promatraju stvari u analizi. No bar u početku bilo bi dobro striktno se držati definicijâ. A reći da sinus nije neprekidan u 0 samo zato što mu domena nije oblika I\.{0} je prilično silly.  |
Op't kvac'ca.  
| veky (napisa): |
 Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza. Onda možda kao neka napomena, ali u svakom slučaju ne kao glavna linija dokaza. |
To je bila i namjera, samo sto to nisam istaknuo jer ne volim boldati simboliku, a nije mi se dalo sad to ici zaokruzivati ili neke slicne perverzije raditi. 
| veky (napisa): | | Ili bar napiši: "uz eps:=|x|+|y| (ili što već), ..." |
Ma nije bitno. Pusti epsilon da pociva u miru. 
| veky (napisa): |
  |
Aleluja! 
| veky (napisa): |
Tome i služe zagrade, no ne moraju zato biti raznih oblikâ. ;-o |
Hehe, okej. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 2:37 sub, 18. 12. 2004 Naslov: Postano: 2:37 sub, 18. 12. 2004 Naslov: |
    |
|
|
[quote="Smith"]Jako sam se zurio (stvar uzasno sporo napreduje), pa nisam narocito pedantan - samo sam prekucao dokaze bez puno razmisljanja. :oops:
Veky ce ovaj put imati puno vise posla kod ispravljanja... :wink:
[/quote]
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
Dokaz T1.7. Skup S je odozDo omeđen, valjda.
Oznaka [latex]\forall-x\in-S[/latex] really *****, IMNSHO. Argument kvantifikacije je varijabla, ne izraz. Bar (-x) stavi u zagrade.
"sup-S"u bi također dobro došle neke zagrade, tipa sup(-S) . Čisto da se vidi da je minus unarni, a ne binarni...
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
Dokaz T1.8. Ako već pišeš sve prilično formalno, daj piši konjunkciju kao konjunkciju, a ne kao zarez. [latex](\forall n\in{\bf N})(a_n\leq a_{n+1}\wedge\ldots[/latex]
"Neka je m=k. Tad je očito." se može puno ljepše reći "za m=k, to je očito." - i bolje će se uklopiti u nastavak.
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m<=k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m<=a_k<=b_k .
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b] .
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
D(Prop1.12): "Analogno je moguće dokazati da _analogna_ (ili "slična", ili nešto takvo) tvrdnja vrijedi i za padajući/strogo padajući/..."
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 )
Dokaz ovog pod 2 je očito pisan u ogromnoj brzini (totalno blesavi tipfeleri), pa ću te pustiti da to sam poispravljaš. :-)
Pod 3, nije previše jasno što je dokaz. Na mjestu na kojem za ostale tvrdnje pišu dokazi, ovdje stoji samo specijalan slučaj (i kombinacija toga sa zbrojem). Možda ipak napisati "(3) vrijedi kao specijalni slučaj od (2), jer je (lambda)_n konstantan niz limesa lambda."
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1 .
4, vidi 2 gore. :-p
5, nije lim već \lim .
I to je zasad to. Očekujem nov, sensible dokaz Prop1.10, i ispravljene sitne gluposti u D(T.1.15.{2&4}) . Onda pričamo dalje. :-)
| Smith (napisa): | Jako sam se zurio (stvar uzasno sporo napreduje), pa nisam narocito pedantan - samo sam prekucao dokaze bez puno razmisljanja. 
Veky ce ovaj put imati puno vise posla kod ispravljanja... 
|
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
Dokaz T1.7. Skup S je odozDo omeđen, valjda.
Oznaka 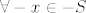 really *****, IMNSHO. Argument kvantifikacije je varijabla, ne izraz. Bar (-x) stavi u zagrade. really *****, IMNSHO. Argument kvantifikacije je varijabla, ne izraz. Bar (-x) stavi u zagrade.
"sup-S"u bi također dobro došle neke zagrade, tipa sup(-S) . Čisto da se vidi da je minus unarni, a ne binarni...
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
Dokaz T1.8. Ako već pišeš sve prilično formalno, daj piši konjunkciju kao konjunkciju, a ne kao zarez. 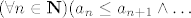
"Neka je m=k. Tad je očito." se može puno ljepše reći "za m=k, to je očito." - i bolje će se uklopiti u nastavak.
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m⇐k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m⇐a_k⇐b_k .
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b] .
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
D(Prop1.12): "Analogno je moguće dokazati da _analogna_ (ili "slična", ili nešto takvo) tvrdnja vrijedi i za padajući/strogo padajući/..."
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 )
Dokaz ovog pod 2 je očito pisan u ogromnoj brzini (totalno blesavi tipfeleri), pa ću te pustiti da to sam poispravljaš. 
Pod 3, nije previše jasno što je dokaz. Na mjestu na kojem za ostale tvrdnje pišu dokazi, ovdje stoji samo specijalan slučaj (i kombinacija toga sa zbrojem). Možda ipak napisati "(3) vrijedi kao specijalni slučaj od (2), jer je (lambda)_n konstantan niz limesa lambda."
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1 .
4, vidi 2 gore. :-p
5, nije lim već \lim .
I to je zasad to. Očekujem nov, sensible dokaz Prop1.10, i ispravljene sitne gluposti u D(T.1.15.{2&4}) . Onda pričamo dalje. 
Zadnja promjena: veky; 16:09 sub, 18. 12. 2004; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 12:19 sub, 18. 12. 2004 Naslov: Postano: 12:19 sub, 18. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
[/quote]
Pa ne mislis valjda da sam digao ruke, zaboga!
Radi se o tome da to mora biti gotovo sto prije, a ne kad pocnu ispiti!
Da pokusas rekonstruirati te dezorijentirane dokaze iz analize iz necije biljeznice s MA1 (ovo sto pise u podsjetniku je jos uvijek ublazena verzija napravljenog na nastavi), shvatio bi o cemu pricam.
Vec i ovako je dovoljno kripticno, istina... Trebalo mi je nekoliko sati za dodati sto sam dodao.
[quote="veky"]
Dokaz T1.7. Skup S je odozDo omeđen, valjda.
[/quote]
Fixed. :oops:
[quote="veky"]
Oznaka [latex]\forall-x\in-S[/latex] really *****, IMNSHO.
[/quote]
Pazi, Nesi bi nas mogla benati zbog ovako teskih rijeci... :wink:
Inace, ne svida se bas ni meni, ali opet - prof. Guljas ju uvodi zbog naseg lakseg shvacanja.
Valjda.
[quote="veky"]
Argument kvantifikacije je varijabla, ne izraz. Bar (-x) stavi u zagrade.
"sup-S"u bi također dobro došle neke zagrade, tipa sup(-S) . Čisto da se vidi da je minus unarni, a ne binarni...
[/quote]
Done. 8)
[quote="veky"]
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
[/quote]
Ima ljepsi nacin, check it out. :)
[quote="veky"]
Dokaz T1.8. Ako već pišeš sve prilično formalno, daj piši konjunkciju kao konjunkciju, a ne kao zarez. [latex](\forall n\in{\bf N})(a_n\leq a_{n+1}\wedge\ldots[/latex]
[/quote]
Whoops, pobjeglo mi. :oops:
Inace, ne cini li ti se ljepse i logicnije pisati \lili nego \klin? :D
[quote="veky"]
"Neka je m=k. Tad je očito." se može puno ljepše reći "za m=k, to je očito." - i bolje će se uklopiti u nastavak.
[/quote]
Okej.
[quote="veky"]
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m<=k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m<=a_k<=b_k .
[/quote]
Provjeri je li sad u redu.
[quote="veky"]
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
[/quote]
Okej, samo da smislim.
[quote="veky"]
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b].
[/quote]
Nisam ovo bas shvatio... Pa naravno da izmedu svaka realna broja postoji barem jedan realan broj (tj. njih beskonacno, kako god).
Primijeti da je a_m razlicit od b_m za svaki m.
[quote="veky"]
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
[/quote]
Mda. Nemoj reci: "Ne'oj tak'." :?
Reci kako! :D
[quote="veky"]
D(Prop1.12): "Analogno je moguće dokazati da _analogna_ (ili "slična", ili nešto takvo) tvrdnja vrijedi i za padajući/strogo padajući/..."
[/quote]
Moze.
[quote="veky"]
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
[/quote]
Slazem se. Done.
[quote="veky"]U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 )[/quote]
Prihvacam bilo koji prijedlog koji osigurava da se prvi red nalazi u $$, a ne cini gadan razmak izmedu brojcice i prvog reda u diviaju (imaj na umu da se LaTeX-u radi).
[quote="veky"]
Dokaz ovog pod 2 je očito pisan u ogromnoj brzini (totalno blesavi tipfeleri), pa ću te pustiti da to sam poispravljaš. :-)[/quote]
Isusek... :oops: :oops: :oops: ad infinitum.
[quote="veky"]
Pod 3, nije previše jasno što je dokaz. Na mjestu na kojem za ostale tvrdnje pišu dokazi, ovdje stoji samo specijalan slučaj (i kombinacija toga sa zbrojem). Možda ipak napisati "(3) vrijedi kao specijalni slučaj od (2), jer je (lambda)_n konstantan niz limesa lambda."
[/quote]
Ok, jesam.
[quote="veky"]
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1.
[/quote]
Ako si htio reci -1, onda kuzim. :wink:
Inace pojasni. :D
[quote="veky"]
4, vidi 2 gore. :-p
[/quote]
Sad okej?
[quote="veky"]
5, nije lim već \lim .
[/quote]
Slazem se. :D
[quote="veky"]
I to je zasad to. Očekujem nov, sensible dokaz Prop1.10, i ispravljene sitne gluposti u D(T.1.15.{2&4}) . Onda pričamo dalje. :-)[/quote]
Stay tuned. :D
| veky (napisa): |
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
|
Pa ne mislis valjda da sam digao ruke, zaboga!
Radi se o tome da to mora biti gotovo sto prije, a ne kad pocnu ispiti!
Da pokusas rekonstruirati te dezorijentirane dokaze iz analize iz necije biljeznice s MA1 (ovo sto pise u podsjetniku je jos uvijek ublazena verzija napravljenog na nastavi), shvatio bi o cemu pricam.
Vec i ovako je dovoljno kripticno, istina... Trebalo mi je nekoliko sati za dodati sto sam dodao.
| veky (napisa): |
Dokaz T1.7. Skup S je odozDo omeđen, valjda.
|
Fixed. 
| veky (napisa): |
Oznaka 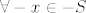 really *****, IMNSHO. really *****, IMNSHO.
|
Pazi, Nesi bi nas mogla benati zbog ovako teskih rijeci... 
Inace, ne svida se bas ni meni, ali opet - prof. Guljas ju uvodi zbog naseg lakseg shvacanja.
Valjda.
| veky (napisa): |
Argument kvantifikacije je varijabla, ne izraz. Bar (-x) stavi u zagrade.
"sup-S"u bi također dobro došle neke zagrade, tipa sup(-S) . Čisto da se vidi da je minus unarni, a ne binarni...
|
Done. 
| veky (napisa): |
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
|
Ima ljepsi nacin, check it out. 
| veky (napisa): |
Dokaz T1.8. Ako već pišeš sve prilično formalno, daj piši konjunkciju kao konjunkciju, a ne kao zarez. 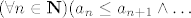
|
Whoops, pobjeglo mi. 
Inace, ne cini li ti se ljepse i logicnije pisati \lili nego \klin? 
| veky (napisa): |
"Neka je m=k. Tad je očito." se može puno ljepše reći "za m=k, to je očito." - i bolje će se uklopiti u nastavak.
|
Okej.
| veky (napisa): |
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m⇐k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m⇐a_k⇐b_k .
|
Provjeri je li sad u redu.
| veky (napisa): |
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
|
Okej, samo da smislim.
| veky (napisa): |
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b].
|
Nisam ovo bas shvatio... Pa naravno da izmedu svaka realna broja postoji barem jedan realan broj (tj. njih beskonacno, kako god).
Primijeti da je a_m razlicit od b_m za svaki m.
| veky (napisa): |
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
|
Mda. Nemoj reci: "Ne'oj tak'." 
Reci kako! 
| veky (napisa): |
D(Prop1.12): "Analogno je moguće dokazati da _analogna_ (ili "slična", ili nešto takvo) tvrdnja vrijedi i za padajući/strogo padajući/..."
|
Moze.
| veky (napisa): |
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
|
Slazem se. Done.
| veky (napisa): | | U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 ) |
Prihvacam bilo koji prijedlog koji osigurava da se prvi red nalazi u $$, a ne cini gadan razmak izmedu brojcice i prvog reda u diviaju (imaj na umu da se LaTeX-u radi).
| veky (napisa): |
Dokaz ovog pod 2 je očito pisan u ogromnoj brzini (totalno blesavi tipfeleri), pa ću te pustiti da to sam poispravljaš.  |
Isusek...    ad infinitum. ad infinitum.
| veky (napisa): |
Pod 3, nije previše jasno što je dokaz. Na mjestu na kojem za ostale tvrdnje pišu dokazi, ovdje stoji samo specijalan slučaj (i kombinacija toga sa zbrojem). Možda ipak napisati "(3) vrijedi kao specijalni slučaj od (2), jer je (lambda)_n konstantan niz limesa lambda."
|
Ok, jesam.
| veky (napisa): |
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1.
|
Ako si htio reci -1, onda kuzim. 
Inace pojasni. 
| veky (napisa): |
4, vidi 2 gore. :-p
|
Sad okej?
| veky (napisa): |
5, nije lim već \lim .
|
Slazem se. 
| veky (napisa): |
I to je zasad to. Očekujem nov, sensible dokaz Prop1.10, i ispravljene sitne gluposti u D(T.1.15.{2&4}) . Onda pričamo dalje.  |
Stay tuned. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 12:46 sub, 18. 12. 2004 Naslov: Postano: 12:46 sub, 18. 12. 2004 Naslov: |
    |
|
|
:OT:
Pisati pod periskopskim okom Veky-ja je kao ples balerine na šanku punom razjarenih bajkera...nemoguće je nebiti dohvaćen :D ...a opet,u tome je draž,plesati,pardon,pisati nešto vrlo oprezno i provjeravati isto dvadeset puta prije priljepljivanja na forum,a onda kao nagrada-iščekivanje-gdje sam mogao faliti ?:wink:

Pisati pod periskopskim okom Veky-ja je kao ples balerine na šanku punom razjarenih bajkera...nemoguće je nebiti dohvaćen  ...a opet,u tome je draž,plesati,pardon,pisati nešto vrlo oprezno i provjeravati isto dvadeset puta prije priljepljivanja na forum,a onda kao nagrada-iščekivanje-gdje sam mogao faliti ? ...a opet,u tome je draž,plesati,pardon,pisati nešto vrlo oprezno i provjeravati isto dvadeset puta prije priljepljivanja na forum,a onda kao nagrada-iščekivanje-gdje sam mogao faliti ?
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 13:08 sub, 18. 12. 2004 Naslov: Postano: 13:08 sub, 18. 12. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]
a opet,u tome je draž,plesati,pardon,pisati nešto vrlo oprezno i provjeravati isto dvadeset puta prije priljepljivanja na forum[/quote]
Gle, sve je to ok, ali za to nema vremena, treba sve proci. (Veky, sjecas se kad si mi rekao nesto vrrrlo slicno? :()
Tu se uopce ne radi o mom _utrosenom_ vremenu.
Radi se iskljucivo o _preostalom_ vremenu koje ja imam za ovo napraviti.
Ako dovrsim posao dva dana prije ispita, koja je korist?
Da mi to pitanje ne predstavlja Damoklov mac, vrlo bih pedantno otklanjao (inace sam perfekcionist sto se toga tice... i da - znam da se iz prilozenog ne vidi) i najsitnije pravopisne i texnicke gr(j)eske.
Mozda da netko kome se da pretipka teorem-dva barem u MathSCII ili neki krajnje bezvezan zapis ako vec ne zna LaTeX, pa ja to pretocim u nj? Cisto zbog lakseg stizanja, ne moje lijenosti.
BAIM, I'll do my best. 8)
Hopefully it will have been shown to have been good enough. :wink:
| Vincent Van Ear (napisa): |
a opet,u tome je draž,plesati,pardon,pisati nešto vrlo oprezno i provjeravati isto dvadeset puta prije priljepljivanja na forum |
Gle, sve je to ok, ali za to nema vremena, treba sve proci. (Veky, sjecas se kad si mi rekao nesto vrrrlo slicno?  ) )
Tu se uopce ne radi o mom _utrosenom_ vremenu.
Radi se iskljucivo o _preostalom_ vremenu koje ja imam za ovo napraviti.
Ako dovrsim posao dva dana prije ispita, koja je korist?
Da mi to pitanje ne predstavlja Damoklov mac, vrlo bih pedantno otklanjao (inace sam perfekcionist sto se toga tice... i da - znam da se iz prilozenog ne vidi) i najsitnije pravopisne i texnicke gr(j)eske.
Mozda da netko kome se da pretipka teorem-dva barem u MathSCII ili neki krajnje bezvezan zapis ako vec ne zna LaTeX, pa ja to pretocim u nj? Cisto zbog lakseg stizanja, ne moje lijenosti.
BAIM, I'll do my best. 
Hopefully it will have been shown to have been good enough. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 16:54 sub, 18. 12. 2004 Naslov: Postano: 16:54 sub, 18. 12. 2004 Naslov: |
    |
|
|
[quote="Smith"][quote="veky"]
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
[/quote]
Pa ne mislis valjda da sam digao ruke, zaboga!
Radi se o tome da to mora biti gotovo sto prije, a ne kad pocnu ispiti!
Da pokusas rekonstruirati te dezorijentirane dokaze iz analize iz necije biljeznice s MA1 (ovo sto pise u podsjetniku je jos uvijek ublazena verzija napravljenog na nastavi), shvatio bi o cemu pricam.[/quote]
Gle, Smith... ja sam ti prvi rekao da si si zadao nemoguću misiju... :-/ Ako želiš moj savjet, radije piši u svoje bilježnice, svojom notacijom, nesputano, tako da samo tebi bude jasno. A onda, _ako ti ostane vremena_, pretači to u LaTeX , pripitomi notaciju, i stavljaj na web...
_nije_ dupli posao. InFact, za jednog perfekcionista poput tebe, to je jedini način na koji možeš ovo raditi a da ne poludiš. ;-)
[quote]Vec i ovako je dovoljno kripticno, istina... Trebalo mi je nekoliko sati za dodati sto sam dodao.[/quote]
As I said. Za napisati to u svojoj bilježnici, daleko od očiju javnosti, dovoljno precizno da znaš _zaista_ rekonstruirati dokaze iz toga, bilo bi ti dovoljno pola sata, IMO. Najviše sat, a još bi (uvjeren sam) i propozicija 1.10 imala pametnije sročen dokaz. ;-)
[quote]Inace, ne svida se bas ni meni, ali opet - prof. Guljas ju uvodi zbog naseg lakseg shvacanja.
Valjda.[/quote]
Ovakve stvari također spadaju u ovo što gore rekoh. Da pišeš samo za sebe, ne bi morao brinuti oko ovakvih stvari...
[quote][quote="veky"]
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
[/quote]
Ima ljepsi nacin, check it out. :)[/quote]
Grozan način, IMO. Nemam ništa protiv egzotične notacije, ali
1)pseudojezik is _not_ a way to go, in the long term
2)_pogotovo u analizi_, strelice se već koriste za stvarno sve i svašta. Imam osjećaj da ćeš jednom požaliti što si ih koristio za ovakve stvari u početku...(*)
3)nije mi baš previše jasno što je ružno u ":="?
[quote]Inace, ne cini li ti se ljepse i logicnije pisati \lili nego \klin? :D[/quote]
Nisam skužio što hoćeš reći. "\wedge", koliko ja znam, koliko god čudno zvučao, jest standardni LaTeX za "and".
[quote][quote="veky"]
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m<=k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m<=a_k<=b_k .
[/quote]
Provjeri je li sad u redu.[/quote]
Sad je u redu ovo što ja pričah, ali sad izlazi na vidjelo da uopće nije jasno je li ovo m<=k zaista BSOMP. Naime, druga grana onda izgleda m>k=>[a_m,b_m]C=[a_k,b_k]=>a_m<=b_m<=b_k , i način zaključivanja je ipak slightly drugačiji. No dobro, stvarno ništa bitno. Samo htjedoh reći da bih ja stavio oba slučaja, tim više što stvarno nisu veliki. No može i ovo.
[quote][quote="veky"]
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
[/quote]
Okej, samo da smislim.[/quote]
Evo ti jedan zgodan:
prvo dokažeš (nešto što bi ti moglo trebati i inače) da je skup X prebrojiv akko postoji injekcija : X/->|N (pogledaš definiciju prebrojivosti. Ako je beskonačan, postoji čak bijekcija s |N , a ako je konačan, postoji bijekcija s nekim [1..n] , koji je podskup od |N . Kad kodomenu te bijekcije proširimo na |N , surjektivnost se gubi, ali injektivnost ostaje, jer ne ovisi o kodomeni samoj.)
E sad, ako je A prebrojiv, imaš injekciju f:A/->|N . Ako je B podskup od A , samo restringiraš f|_B . Restrikcija injekcije je injekcija, naravno. :-)
[quote][quote="veky"]
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b].
[/quote]
Nisam ovo bas shvatio... Pa naravno da izmedu svaka realna broja postoji barem jedan realan broj (tj. njih beskonacno, kako god).[/quote]
Hm... ma ne to.
Cantorov teorem (T1.8 ) ti kaže "postoji x@|R takav da je u svakom [a_ž,b_ž] ". Pitah, kako znaš da je taj x u [a,b] . No dobro, [a,b] jest jedan od tih segmenata (prvi), pa se vidi. ok.
[quote]Primijeti da je a_m razlicit od b_m za svaki m.[/quote]
Čak i da nije, svejedno bi x postojao. :-)
[quote][quote="veky"]
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
[/quote]
Mda. Nemoj reci: "Ne'oj tak'." :?
Reci kako! :D[/quote]
Pa piše. "da ne postoji _n takav da je_ f(n)=x"
Tamo kod tebe piše "da ne postoji f(n)=x". x postoji, valjda. :-)
[quote][quote="veky"]
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
[/quote]
Slazem se. Done.[/quote]
Done? Ne bih rekao. :-/
_u izreci_, mislim. U dokazu si to stvarno napravio, no ne treba ti toliki scope. Ne moraš za svaki n tvrditi da je b!=0 . :-)
[quote][quote="veky"]U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 )[/quote]
Prihvacam bilo koji prijedlog koji osigurava da se prvi red nalazi u $$, a ne cini gadan razmak izmedu brojcice i prvog reda u diviaju (imaj na umu da se LaTeX-u radi).[/quote]
GadanRazmak je sasvim ok, ako ga popuniš nečim. Ionako nije stilski dobro započeti sa simbolima odmah nakon "1." (što je također simbolika, iz jednog drugog svijeta). Recimo
"1. Zbog konvergentnosti od (a_n)_n i (b_n)_n imamo
$$...$$
$$...$$"
A kao bonus ćeš dobiti i pravo centriranje. ;-)
[quote][quote="veky"]
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1.
[/quote]
Ako \true, onda kuzim. :wink:[/quote]
Evo, o ovome pričah tamo kod [*] gore... u jednom redu pričaš o konvergenciji konstantnog niza (lambda)_n k lambda, a u sljedećem redu pišeš nešto što valjda 80% ljudi, u tom mindsettingu, počnu čitati kao "lambda teži k -1 ... ma ne, -1 teži k lambda... ma ne... o čemu ovaj, dovvaga?"
Shvaćaš?
[quote][quote="veky"]
4, vidi 2 gore. :-p
[/quote]
Sad okej?[/quote]
Ne. :-p Još ti fale na dva mjesta oznake za apsolutnu vrijednost. b_n-b , i b/2 .
[quote]Stay tuned. :D[/quote]
Naravno. Sam si to tražio. ;-)
| Smith (napisa): | | veky (napisa): |
Kao što rekoh, baš me zanima koliko ćeš dugo izdržati. ;-/
|
Pa ne mislis valjda da sam digao ruke, zaboga!
Radi se o tome da to mora biti gotovo sto prije, a ne kad pocnu ispiti!
Da pokusas rekonstruirati te dezorijentirane dokaze iz analize iz necije biljeznice s MA1 (ovo sto pise u podsjetniku je jos uvijek ublazena verzija napravljenog na nastavi), shvatio bi o cemu pricam. |
Gle, Smith... ja sam ti prvi rekao da si si zadao nemoguću misiju... :-/ Ako želiš moj savjet, radije piši u svoje bilježnice, svojom notacijom, nesputano, tako da samo tebi bude jasno. A onda, _ako ti ostane vremena_, pretači to u LaTeX , pripitomi notaciju, i stavljaj na web...
_nije_ dupli posao. InFact, za jednog perfekcionista poput tebe, to je jedini način na koji možeš ovo raditi a da ne poludiš. 
| Citat: | | Vec i ovako je dovoljno kripticno, istina... Trebalo mi je nekoliko sati za dodati sto sam dodao. |
As I said. Za napisati to u svojoj bilježnici, daleko od očiju javnosti, dovoljno precizno da znaš _zaista_ rekonstruirati dokaze iz toga, bilo bi ti dovoljno pola sata, IMO. Najviše sat, a još bi (uvjeren sam) i propozicija 1.10 imala pametnije sročen dokaz. 
| Citat: | Inace, ne svida se bas ni meni, ali opet - prof. Guljas ju uvodi zbog naseg lakseg shvacanja.
Valjda. |
Ovakve stvari također spadaju u ovo što gore rekoh. Da pišeš samo za sebe, ne bi morao brinuti oko ovakvih stvari...
| Citat: | | veky (napisa): |
Ako već uvodiš novu oznaku L usred retka dokaza, bilo bi dobro to označiti, kao (-x<L:=sup(-S)) na primjer.
|
Ima ljepsi nacin, check it out.  |
Grozan način, IMO. Nemam ništa protiv egzotične notacije, ali
1)pseudojezik is _not_ a way to go, in the long term
2)_pogotovo u analizi_, strelice se već koriste za stvarno sve i svašta. Imam osjećaj da ćeš jednom požaliti što si ih koristio za ovakve stvari u početku...(*)
3)nije mi baš previše jasno što je ružno u ":="?
| Citat: | Inace, ne cini li ti se ljepse i logicnije pisati \lili nego \klin?  |
Nisam skužio što hoćeš reći. "\wedge", koliko ja znam, koliko god čudno zvučao, jest standardni LaTeX za "and".
| Citat: | | veky (napisa): |
Nego, stvarno ne vidim što će ti ovo natjeravanje p-ova... jednostavno, po tranzitivnosti relacije "C=", imaš da je (za m⇐k , pa čak ne moraš ni gornji poseban slučaj imati) [a_k,b_k]C=[a_m,b_m] , pa je a_m⇐a_k⇐b_k .
|
Provjeri je li sad u redu. |
Sad je u redu ovo što ja pričah, ali sad izlazi na vidjelo da uopće nije jasno je li ovo m⇐k zaista BSOMP. Naime, druga grana onda izgleda m>k⇒[a_m,b_m]C=[a_k,b_k]⇒a_m⇐b_m⇐b_k , i način zaključivanja je ipak slightly drugačiji. No dobro, stvarno ništa bitno. Samo htjedoh reći da bih ja stavio oba slučaja, tim više što stvarno nisu veliki. No može i ovo.
| Citat: | | veky (napisa): |
Prop1.10. Neprazan istaknuto?? Zašto? Zar prazan skup ne smatrate prebrojivim? :-/
A dokaz je totalni mišmaš. Nema uopće smisla ovdje nešto pisati, dođi do mene pa da to riješimo. :-p Ili napiši sam nešto što ima smisla...
|
Okej, samo da smislim. |
Evo ti jedan zgodan:
prvo dokažeš (nešto što bi ti moglo trebati i inače) da je skup X prebrojiv akko postoji injekcija : X/→|N (pogledaš definiciju prebrojivosti. Ako je beskonačan, postoji čak bijekcija s |N , a ako je konačan, postoji bijekcija s nekim [1..n] , koji je podskup od |N . Kad kodomenu te bijekcije proširimo na |N , surjektivnost se gubi, ali injektivnost ostaje, jer ne ovisi o kodomeni samoj.)
E sad, ako je A prebrojiv, imaš injekciju f:A/→|N . Ako je B podskup od A , samo restringiraš f|_B . Restrikcija injekcije je injekcija, naravno. 
| Citat: | | veky (napisa): |
Dokaz T1.11: kako znaš da je x@[a,b] ? Cantorov teorem ti daje da je x@|R . Možda je dobro reći, specijalno za n=1 , x@[a_1,b_1]=[a,b].
|
Nisam ovo bas shvatio... Pa naravno da izmedu svaka realna broja postoji barem jedan realan broj (tj. njih beskonacno, kako god). |
Hm... ma ne to.
Cantorov teorem (T1.8 ) ti kaže "postoji x@|R takav da je u svakom [a_ž,b_ž] ". Pitah, kako znaš da je taj x u [a,b] . No dobro, [a,b] jest jedan od tih segmenata (prvi), pa se vidi. ok.
| Citat: | | Primijeti da je a_m razlicit od b_m za svaki m. |
Čak i da nije, svejedno bi x postojao. 
| Citat: | | veky (napisa): |
"našli smo x takav da ne postoji _što_"? Grozan wording. "...da ne postoji n takav da je f(n)=x ".
|
Mda. Nemoj reci: "Ne'oj tak'." 
Reci kako!  |
Pa piše. "da ne postoji _n takav da je_ f(n)=x"
Tamo kod tebe piše "da ne postoji f(n)=x". x postoji, valjda. 
| Citat: | | veky (napisa): |
T1.15.4. Možda bi bilo dobro reći ...b_n!=0 _za svaki n_... .
|
Slazem se. Done. |
Done? Ne bih rekao. :-/
_u izreci_, mislim. U dokazu si to stvarno napravio, no ne treba ti toliki scope. Ne moraš za svaki n tvrditi da je b!=0 . 
| Citat: | | veky (napisa): | | U dokazu ovog pod 1 , jesi li svjestan toga da ti je jedan redak $ , a drugi $$ ? (vidi se po razlomku eps/2 ) |
Prihvacam bilo koji prijedlog koji osigurava da se prvi red nalazi u $$, a ne cini gadan razmak izmedu brojcice i prvog reda u diviaju (imaj na umu da se LaTeX-u radi). |
GadanRazmak je sasvim ok, ako ga popuniš nečim. Ionako nije stilski dobro započeti sa simbolima odmah nakon "1." (što je također simbolika, iz jednog drugog svijeta). Recimo
"1. Zbog konvergentnosti od (a_n)_n i (b_n)_n imamo
$$...$$
$$...$$"
A kao bonus ćeš dobiti i pravo centriranje. 
| Citat: | | veky (napisa): |
A specijalni slučaj označiti kao specijalni slučaj... ako već nikako drugačije, bar lambda:=1.
|
Ako \true, onda kuzim.  |
Evo, o ovome pričah tamo kod [*] gore... u jednom redu pričaš o konvergenciji konstantnog niza (lambda)_n k lambda, a u sljedećem redu pišeš nešto što valjda 80% ljudi, u tom mindsettingu, počnu čitati kao "lambda teži k -1 ... ma ne, -1 teži k lambda... ma ne... o čemu ovaj, dovvaga?"
Shvaćaš?
| Citat: | | veky (napisa): |
4, vidi 2 gore. :-p
|
Sad okej? |
Ne. :-p Još ti fale na dva mjesta oznake za apsolutnu vrijednost. b_n-b , i b/2 .
| Citat: | Stay tuned.  |
Naravno. Sam si to tražio. 
|
|
| [Vrh] |
|
|
















