| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
z e^ix
Forumaš(ica)

Pridružen/a: 16. 09. 2003. (17:44:45)
Postovi: (B)16
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
n0mad
Forumaš(ica)


Pridružen/a: 16. 02. 2004. (12:58:32)
Postovi: (B3)16
|
|
| [Vrh] |
|
z e^ix
Forumaš(ica)

Pridružen/a: 16. 09. 2003. (17:44:45)
Postovi: (B)16
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
bily
Forumaš(ica)


Pridružen/a: 29. 04. 2003. (16:21:46)
Postovi: (4B7)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:28 pon, 4. 7. 2005 Naslov: Postano: 2:28 pon, 4. 7. 2005 Naslov: |
    |
|
|
[color=darkred]Vec vidim kuda ovo vodi, pa zato: [b]ne upustajte se u svadje[/b] (ako bas zelite, imate PM). [b]Radije pomozite covjeku[/b] (meni je ODJ jako shepao, pa se ne sjecam tih stvari :oops:).[/color]
Vec vidim kuda ovo vodi, pa zato: ne upustajte se u svadje (ako bas zelite, imate PM). Radije pomozite covjeku (meni je ODJ jako shepao, pa se ne sjecam tih stvari  ). ).
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
z e^ix
Forumaš(ica)

Pridružen/a: 16. 09. 2003. (17:44:45)
Postovi: (B)16
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 1:10 čet, 7. 7. 2005 Naslov: Postano: 1:10 čet, 7. 7. 2005 Naslov: |
    |
|
|
Okej -- nije bas jednostavan odgovor no sljedece vrijedi:
Za [latex]f\in C^1(\hbox{\bf R})[/latex] vrijedi (vrijedi i sire, ovo je samo pokazno):
[latex]d_x\vec y=f'(x)d_x\vec x \Leftrightarrow f(x)=f(0)+\int_0^x d_\xi y d\xi[/latex],
pri cemu je [latex]d=d_\xi:\mathop{\hbox{\bf R}}\nolimits^2\rightarrow \hbox{\bf R}[/latex] definiran sa [latex]d=d_\xi: \vec a\mapsto \langle \vec a| (1,f'(\xi))\rangle[/latex], [latex]f'(x)={d\over dx}f(x)=\lim\limits_{\epsilon\to0}{f(x+\epsilon)-f(x)\over \epsilon}[/latex], te [latex]\vec y=(0,1)[/latex] i [latex]\vec x=(1,0)[/latex]
Dokaz (skica?):
[latex]d_x\vec y=\langle (0,1)| (1,f'(x))\rangle=f'(x)=f'(x)\cdot 1=f'(x)\langle (1,0)| (1,f'(\xi))\rangle=f'(x)d_x \vec x [/latex],
iz cega slijedi [latex]{d_x\vec y\over d_x\vec x}=f'(x)d_x[/latex]
[latex]f(x)-f(0)=\int\limits_0^x f'(\xi)d\xi=\int\limits_0^x f'(\xi)d_\xi\vec xd\xi=\int\limits_0^x d_\xi yd\xi[/latex]
Q.E.D. :)
Zapravo, cijela ova prica svodi se na sljedece: imamo puuuno vrsta malih slova [latex]d[/latex]. Imamo [latex]d[/latex] u diferencijalu, [latex]{d\over d\hbox{\v z}}[/latex], imamo [latex]d[/latex] u diferencijalnim formama [latex]\phi(x,y)dx+\psi(x,y)dy=0[/latex], koji je sasvim nesto drugo, onda imamo opet [latex]d[/latex] pod integralom, koji je pak nesto trece i tako dalje i tako dalje i -- tako dalje. poanta je -- svi su oni.. hmph.. ekvivalentni.
Odakle ona definicija [latex]d_x[/latex] i zasto trebamo [latex]x[/latex] u indeksu? Tu se nalazi kljuc cijele stvari -- imamo graf funkcije u euklidskoj ravnini [latex]\hbox{\bf R}^2[/latex]. Svakoj tocki tog grafa mozemo pridruziti jedan cijeli vektorski prostor -- pravac, tangentu,
[latex]T\Gamma_f(x)=\left\{\lambda(1,f'(x)): \lambda\in\hbox{\bf R}\right\}[/latex]. E, sada, [latex]d_x[/latex] smo zapravo definirali kao linearni funkcional koji nam daje duljinu projekcije vektora iz [latex]\hbox{\bf R}^2[/latex] u [latex]T\Gamma_f(x)[/latex]. Ono sto je zgodno -- mi u definiciji nismo koristili normirani vektor, no to nije problem, zato sto na kraju zelimo dobiti formu razlomka, pa nam se ta skala pokrati.
Eto, nadam se da je sada ikome osim meni jasnije.
'ave fun!
Sinisa
Okej – nije bas jednostavan odgovor no sljedece vrijedi:
Za 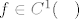 vrijedi (vrijedi i sire, ovo je samo pokazno): vrijedi (vrijedi i sire, ovo je samo pokazno):
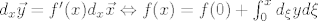 , ,
pri cemu je 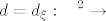 definiran sa definiran sa 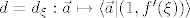 , , 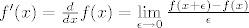 , te , te 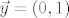 i i 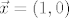
Dokaz (skica?):
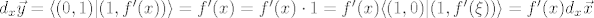 , ,
iz cega slijedi 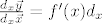
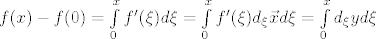
Q.E.D. 
Zapravo, cijela ova prica svodi se na sljedece: imamo puuuno vrsta malih slova  . Imamo . Imamo  u diferencijalu, u diferencijalu, 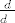 , imamo , imamo 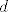 u diferencijalnim formama u diferencijalnim formama 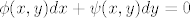 , koji je sasvim nesto drugo, onda imamo opet , koji je sasvim nesto drugo, onda imamo opet 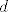 pod integralom, koji je pak nesto trece i tako dalje i tako dalje i – tako dalje. poanta je – svi su oni.. hmph.. ekvivalentni. pod integralom, koji je pak nesto trece i tako dalje i tako dalje i – tako dalje. poanta je – svi su oni.. hmph.. ekvivalentni.
Odakle ona definicija 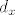 i zasto trebamo i zasto trebamo  u indeksu? Tu se nalazi kljuc cijele stvari – imamo graf funkcije u euklidskoj ravnini u indeksu? Tu se nalazi kljuc cijele stvari – imamo graf funkcije u euklidskoj ravnini  . Svakoj tocki tog grafa mozemo pridruziti jedan cijeli vektorski prostor – pravac, tangentu, . Svakoj tocki tog grafa mozemo pridruziti jedan cijeli vektorski prostor – pravac, tangentu,
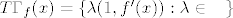 . E, sada, . E, sada, 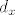 smo zapravo definirali kao linearni funkcional koji nam daje duljinu projekcije vektora iz smo zapravo definirali kao linearni funkcional koji nam daje duljinu projekcije vektora iz  u u 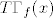 . Ono sto je zgodno – mi u definiciji nismo koristili normirani vektor, no to nije problem, zato sto na kraju zelimo dobiti formu razlomka, pa nam se ta skala pokrati. . Ono sto je zgodno – mi u definiciji nismo koristili normirani vektor, no to nije problem, zato sto na kraju zelimo dobiti formu razlomka, pa nam se ta skala pokrati.
Eto, nadam se da je sada ikome osim meni jasnije.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
goc9999
Forumaš(ica)


Pridružen/a: 15. 10. 2003. (19:31:20)
Postovi: (238)16
Spol: 
Lokacija: Utrina
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 18:20 čet, 8. 12. 2005 Naslov: Postano: 18:20 čet, 8. 12. 2005 Naslov: |
    |
|
|
[quote="vili"]Mislim da ovo nema puno veze sa započetim topicom al nek ti bude :wink:
I neću te ispravljat zato jer dobro radiš :) , barem što se tehničkog dijela tiče.
Da pojasnim: To što kažeš je savršeno točno a teorijsku pozadinu množenja sa dx i onda integriranja obje strane je objasnio cinik par postova nagore (i par mjeseci prije :mrgreen: ) i ja se tu neću miješat zato jer se nema šta dodat i naročito zato jer ni ja ne kužim :PP
Barem ono njegovo, a za pozadinu svega malo prolistaj skriptu iz Analize 3 profesora Ungara i prouči parcijalne derivacije i derivacije duž vektora..[/quote]
Nemojte se uopće uzrujavati s tim dx-ovima. Ja sam isto razmisljao o njima na 2. godini, no njihov pravi smisao mi je zapravo postao jasan tek na 4. godini kada se definiraju diferencijalne forme na apstraktnim diferencijalnim mnogostukositma.
One su jako bitne jer se uz pomoć njih definira integral po mnogostrukosti, no to je sad cijela teorija za sebe...
Mislim da je zasad jedino bitno uzeti zdravo za gotovo da se iz nekog razloga s tim dx-ovima može množiti, integrirati i na kraju sve sve dobro ispada, a zašto i kako.. pricekajte... :)
| vili (napisa): | Mislim da ovo nema puno veze sa započetim topicom al nek ti bude 
I neću te ispravljat zato jer dobro radiš  , barem što se tehničkog dijela tiče. , barem što se tehničkog dijela tiče.
Da pojasnim: To što kažeš je savršeno točno a teorijsku pozadinu množenja sa dx i onda integriranja obje strane je objasnio cinik par postova nagore (i par mjeseci prije  ) i ja se tu neću miješat zato jer se nema šta dodat i naročito zato jer ni ja ne kužim ) i ja se tu neću miješat zato jer se nema šta dodat i naročito zato jer ni ja ne kužim 
Barem ono njegovo, a za pozadinu svega malo prolistaj skriptu iz Analize 3 profesora Ungara i prouči parcijalne derivacije i derivacije duž vektora.. |
Nemojte se uopće uzrujavati s tim dx-ovima. Ja sam isto razmisljao o njima na 2. godini, no njihov pravi smisao mi je zapravo postao jasan tek na 4. godini kada se definiraju diferencijalne forme na apstraktnim diferencijalnim mnogostukositma.
One su jako bitne jer se uz pomoć njih definira integral po mnogostrukosti, no to je sad cijela teorija za sebe...
Mislim da je zasad jedino bitno uzeti zdravo za gotovo da se iz nekog razloga s tim dx-ovima može množiti, integrirati i na kraju sve sve dobro ispada, a zašto i kako.. pricekajte... 
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 20:32 čet, 8. 12. 2005 Naslov: Postano: 20:32 čet, 8. 12. 2005 Naslov: |
    |
|
|
[quote="vili"]Tnx za utjehu.[/quote]
you're welcome. :)
pogotovo kad se sjetim kako sam glavu razbijao trazeci striktnomatematicku interpretaciju svakog koraka u zadacima iz ODJ-a i
nesto jesam naslucivao... no u nekom trenutku sam reko, maaa.. mnozi sa dx, pa sta bude bude :lol:
[quote="vili"] Možda bi ti i dirao u karmu da mi ne pada na pamet da nakon 100 ide -101 :wacky:
Enivej, zaintrigirao si me. hau d hel si tolko skupio? Jel to neka greška il je brucošima [b]stvarno[/b] drago zbog dodatnih vježbi? :D[/quote]
:OT:
nemam pojma, valjda je neka greska, ipak mi se cini da nije zato sto "dobro" nadjem prirodnu domenu :lol:
| vili (napisa): | | Tnx za utjehu. |
you're welcome. 
pogotovo kad se sjetim kako sam glavu razbijao trazeci striktnomatematicku interpretaciju svakog koraka u zadacima iz ODJ-a i
nesto jesam naslucivao... no u nekom trenutku sam reko, maaa.. mnozi sa dx, pa sta bude bude 
| vili (napisa): | Možda bi ti i dirao u karmu da mi ne pada na pamet da nakon 100 ide -101 
Enivej, zaintrigirao si me. hau d hel si tolko skupio? Jel to neka greška il je brucošima stvarno drago zbog dodatnih vježbi?  |

nemam pojma, valjda je neka greska, ipak mi se cini da nije zato sto "dobro" nadjem prirodnu domenu 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
|












