|
Kao prvo da razjasnimo notaciju:
[latex]\{Q\leq c\}=\{y\in\mathbf{R}^n : Q(y)\leq c\}[/latex]
Dakle, to je praslika skupa [latex]\langle -\infty,c][/latex] po funkciji [latex]Q\colon\mathbf{R}^n\to\mathbf{R}[/latex].
Kompaktnost tog skupa je ekvivalentna s njegovim ograničenošću i zatvorenošću.
Pretpostavimo dakle da je C pozitivno definitna matrica i dokažimo da je [latex]\{Q\leq c\}[/latex] kompaktan.
Zatvorenost:
Funkcija [latex]Q\colon\mathbf{R}^n\to\mathbf{R}[/latex] je neprekidna (jer je to specijalni polinom u n varijabli), a skup [latex]\langle -\infty,c][/latex] je zatvoren pa je i njegova praslika zatvoren skup u R^n.
Ograničenost:
Ne treba nama nikakva ograda na Q niti Q(y), nego na norme elemenata tog skupa.
Želimo pokazati da se taj skup nalazi u nekoj kugli oko ishodišta radijusa R, a to ćemo pokazati tako da dokažemo da postoji R>0 t.d. vrijedi
[latex]\|y\|\leq R[/latex], za svaki [latex]y\in\{Q\leq c\}[/latex].
Zbog pozitivne definitnosti od C postoji konstanta [latex]\alpha>0[/latex] takva da je
[latex]y^\tau C y=(Cy|y)\geq \alpha\|y\|^2[/latex] za sve [latex]y\in\mathbf{R}^n[/latex].
Sada za [latex]y\in\{Q\leq c\}[/latex] vrijedi:
[latex]\frac{1}{2}\alpha\|y\|^2-\|b\|\cdot\|y\|-|\gamma|\leq Q(y)\leq c[/latex]
Ako su x1<=x2 korijeni kvadratne jednadžbe
[latex]\frac{1}{2}\alpha\cdot x^2-\|b\|\cdot x-|\gamma|-c=0[/latex]
onda mora biti [latex]\|y\|\in[x1,x2][/latex] (skiciraš si parabolu okrenutu prema gore) pa je
[latex]\|y\|\leq R:=\max\{|x1|,|x2|\}[/latex]
Moguće je i da ova kvadratna jednadžba nema realne korijene, ali onda smo dobili kontradikciju s [latex]y\in\{Q\leq c\}[/latex], tj. skup [latex]\{Q\leq c\}[/latex] je prazan pa je opet (trivijalno) ograničen.
(To je zapravo isti dokaz, ali precizno napisan. Ono gore, iz skripte, je stvarno šlampavo.)
--------------------------------------
Sada pretpostavimo da je za neki realni broj c skup [latex]\{Q\leq c\}[/latex] kompaktan i neprazan. Specijalno je ograničen.
Želimo dokazati da je C pozitivno definitna matrica. Podrazumijeva se, valjda iz definicije "kvadratičnog" funkcionala, da je simetrična.
U ovom gore dokazu (iz skripte) je nešto krivo, a i on samo "dokazuje" regularnost od C, a ne i pozitivnost.
Možemo recimo ovako:
Da bismo dokazali da je matrica C pozitivno definitna dovoljno je dokazati da su joj sve svojstvene vrijednosti >0 (znamo da su realne jer je simetrična).
Pretpostavimo suprotno, tj. da je broj [latex]-\lambda_0[/latex] svojstvena vrijednost od C za neki [latex]\lambda_0\geq 0[/latex]. Neka je [latex]y_0[/latex] neki pripadni svojstveni vektor (tj. ne-nul vektor iz pripadnog svojstvenog potprostora). Znamo da je i svaki njegov skalarni višekratnik isto svojstven za [latex]-\lambda_0[/latex] pa dakle možemo pretpostaviti da je njegova norma [latex]\|y_0\|[/latex] dovoljno velika, pri čemu ćemo to "dovoljno velika" uskoro precizirati (u dva navrata). (Mogao bih to odmah napisati, ali bi izgledalo neprirodno.)
Zbog ograničenosti od [latex]\{Q\leq c\}[/latex] postoji R>0 t.d. vrijedi[latex]\|y\|\leq R[/latex], za svaki [latex]y\in\{Q\leq c\}[/latex].
Ako pretpostavimo da smo uzeli [latex]y_0[/latex] takav da je [latex]\|y_0\|>R[/latex] (što smo mogli), onda će biti [latex]y_0\not\in\{Q\leq c\}[/latex], tj. [latex]Q(y_0)>c[/latex].
1.slučaj: [latex]\lambda_0 >0[/latex]
Zbog [latex]Cy_0=-\lambda_0 y_0[/latex] smo dobili:
[latex]-\frac{1}{2}\lambda_0 \|y_0\|^2+b^\tau y_0 +\gamma>c[/latex]
tj.
[latex]\|b\|\cdot\|y_0\| \geq b^\tau y_0>\frac{1}{2}\lambda_0 \|y_0\|^2-\gamma+c>0[/latex]
tj.
[latex]\frac{1}{2}\lambda_0 \|y_0\|^2-\|b\|\cdot\|y_0\| -\gamma+c<0[/latex]
Ako su x1<=x2 korijeni kvadratne jednadžbe (ako pak nema realne korijene onda odmah imamo kontradikciju)
[latex]\frac{1}{2}\lambda_0 \cdot x^2-\|b\|\cdot x -\gamma+c=0[/latex]
onda mora biti [latex]\|y_0\|\in\langle x1,x2\rangle [/latex] (skiciraš si opet parabolu okrenutu prema gore) pa je
[latex]\|y_0\|\leq \max\{|x1|,|x2|\}[/latex]
ali to je kontradikcija ako smo uzeli [latex]y_0[/latex] s dovoljno velikom normom, tj. [latex]\|y_0\|>\max\{|x1|,|x2|\}[/latex], što smo mogli.
2.slučaj: [latex]\lambda_0 =0[/latex]
Imamo [latex]Cy_0=\mathbf{0}[/latex], [latex]Q(y_0)>c[/latex] pa je
[latex]b^\tau y_0 +\gamma>c[/latex]
Sada se sjetimo da smo koristili samo [latex]Cy_0=\mathbf{0}[/latex] i [latex]\|y_0\|>R[/latex] pa možemo [latex]y_0[/latex] zamijeniti s [latex]t y_0[/latex] za neki [latex]t\in\mathbf{R},\ |t|\geq 1[/latex].
[latex]t\cdot b^\tau y_0 >c-\gamma[/latex]
Puštanjem t->-oo, odnosno t->+oo, dobivamo da mora biti [latex]b^\tau y_0=0[/latex].
Zbog proizvoljnosti od y_0 je vektor b okomit na cijelu jezgru N(C) (tj. na sve vektore y_0 iz svojstvenog potprostora pridruženog sv.vrij. 0).
Zbog nepraznosti od [latex]\{Q\leq c\}[/latex] postoji vektor u takav da je Q(u)<=c, tj.
[latex]\frac{1}{2}u^\tau C u+b^\tau u +\gamma\leq c[/latex]
Za svaki y_0 iz N(C) je [latex]Cy_0=\mathbf{0}[/latex], [latex]y_{0}^\tau C=(Cy_0)^\tau=\mathbf{0}[/latex] i [latex]b^\tau y_0=0[/latex] pa imamo i
[latex]\frac{1}{2}(u+y_0)^\tau C (u+y_0)+b^\tau (u+y_0) +\gamma\leq c[/latex]
tj. [latex]u+y_0\in\{Q\leq c\}[/latex]
Zbog spomenute ograničenosti je
[latex]\|u+y_0\|\leq R[/latex]
odakle slijedi
[latex]\|y_0\|\leq R+\|u\|[/latex]
što je kontradikcija jer možemo uzeti y_0 t.d. je
[latex]\|y_0\|> R+\|u\|[/latex].
------------------------
Kažem, ovo su precizni i detaljno raspisani dokazi (makar malo zamršeni). Ako je netko zadovoljan sa šlampavim dokazom ili samo s idejom, onda bolje neka se ne muči s ovim mojim cjepidlačenjima. Mislim da nipošto ne treba pamtiti "račun". Zapravo, sad se pitam da li je ovo ikome korisno. :? Ali barem je dokaz, a ne "dokaz". :) Jedino što ovo sad izgleda kao nešto pametno, a zapravo nije.
Kao prvo da razjasnimo notaciju:
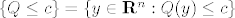
Dakle, to je praslika skupa 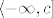 po funkciji po funkciji 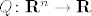 . .
Kompaktnost tog skupa je ekvivalentna s njegovim ograničenošću i zatvorenošću.
Pretpostavimo dakle da je C pozitivno definitna matrica i dokažimo da je 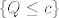 kompaktan. kompaktan.
Zatvorenost:
Funkcija 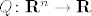 je neprekidna (jer je to specijalni polinom u n varijabli), a skup je neprekidna (jer je to specijalni polinom u n varijabli), a skup 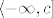 je zatvoren pa je i njegova praslika zatvoren skup u R^n. je zatvoren pa je i njegova praslika zatvoren skup u R^n.
Ograničenost:
Ne treba nama nikakva ograda na Q niti Q(y), nego na norme elemenata tog skupa.
Želimo pokazati da se taj skup nalazi u nekoj kugli oko ishodišta radijusa R, a to ćemo pokazati tako da dokažemo da postoji R>0 t.d. vrijedi
 , za svaki , za svaki 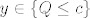 . .
Zbog pozitivne definitnosti od C postoji konstanta 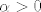 takva da je takva da je
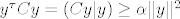 za sve za sve 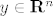 . .
Sada za 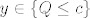 vrijedi: vrijedi:
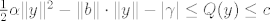
Ako su x1⇐x2 korijeni kvadratne jednadžbe
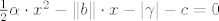
onda mora biti 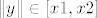 (skiciraš si parabolu okrenutu prema gore) pa je (skiciraš si parabolu okrenutu prema gore) pa je
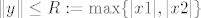
Moguće je i da ova kvadratna jednadžba nema realne korijene, ali onda smo dobili kontradikciju s 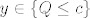 , tj. skup , tj. skup 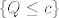 je prazan pa je opet (trivijalno) ograničen. je prazan pa je opet (trivijalno) ograničen.
(To je zapravo isti dokaz, ali precizno napisan. Ono gore, iz skripte, je stvarno šlampavo.)
--------------------------------------
Sada pretpostavimo da je za neki realni broj c skup 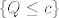 kompaktan i neprazan. Specijalno je ograničen. kompaktan i neprazan. Specijalno je ograničen.
Želimo dokazati da je C pozitivno definitna matrica. Podrazumijeva se, valjda iz definicije "kvadratičnog" funkcionala, da je simetrična.
U ovom gore dokazu (iz skripte) je nešto krivo, a i on samo "dokazuje" regularnost od C, a ne i pozitivnost.
Možemo recimo ovako:
Da bismo dokazali da je matrica C pozitivno definitna dovoljno je dokazati da su joj sve svojstvene vrijednosti >0 (znamo da su realne jer je simetrična).
Pretpostavimo suprotno, tj. da je broj 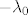 svojstvena vrijednost od C za neki svojstvena vrijednost od C za neki  . Neka je . Neka je 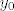 neki pripadni svojstveni vektor (tj. ne-nul vektor iz pripadnog svojstvenog potprostora). Znamo da je i svaki njegov skalarni višekratnik isto svojstven za neki pripadni svojstveni vektor (tj. ne-nul vektor iz pripadnog svojstvenog potprostora). Znamo da je i svaki njegov skalarni višekratnik isto svojstven za 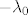 pa dakle možemo pretpostaviti da je njegova norma pa dakle možemo pretpostaviti da je njegova norma 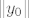 dovoljno velika, pri čemu ćemo to "dovoljno velika" uskoro precizirati (u dva navrata). (Mogao bih to odmah napisati, ali bi izgledalo neprirodno.) dovoljno velika, pri čemu ćemo to "dovoljno velika" uskoro precizirati (u dva navrata). (Mogao bih to odmah napisati, ali bi izgledalo neprirodno.)
Zbog ograničenosti od 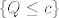 postoji R>0 t.d. vrijedi postoji R>0 t.d. vrijedi , za svaki , za svaki 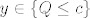 . .
Ako pretpostavimo da smo uzeli 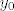 takav da je takav da je 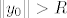 (što smo mogli), onda će biti (što smo mogli), onda će biti 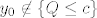 , tj. , tj. 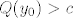 . .
1.slučaj: 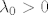
Zbog 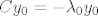 smo dobili: smo dobili:
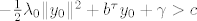
tj.
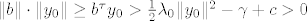
tj.
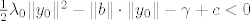
Ako su x1⇐x2 korijeni kvadratne jednadžbe (ako pak nema realne korijene onda odmah imamo kontradikciju)
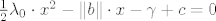
onda mora biti 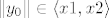 (skiciraš si opet parabolu okrenutu prema gore) pa je (skiciraš si opet parabolu okrenutu prema gore) pa je
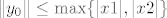
ali to je kontradikcija ako smo uzeli 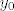 s dovoljno velikom normom, tj. s dovoljno velikom normom, tj. 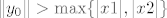 , što smo mogli. , što smo mogli.
2.slučaj: 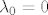
Imamo 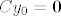 , , 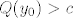 pa je pa je
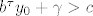
Sada se sjetimo da smo koristili samo 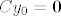 i i 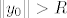 pa možemo pa možemo 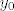 zamijeniti s zamijeniti s 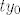 za neki za neki 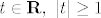 . .
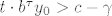
Puštanjem t→-oo, odnosno t→+oo, dobivamo da mora biti 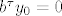 . .
Zbog proizvoljnosti od y_0 je vektor b okomit na cijelu jezgru N(C) (tj. na sve vektore y_0 iz svojstvenog potprostora pridruženog sv.vrij. 0).
Zbog nepraznosti od 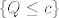 postoji vektor u takav da je Q(u)⇐c, tj. postoji vektor u takav da je Q(u)⇐c, tj.
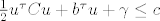
Za svaki y_0 iz N(C) je 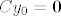 , , 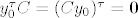 i i 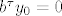 pa imamo i pa imamo i
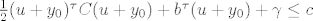
tj. 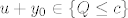
Zbog spomenute ograničenosti je
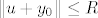
odakle slijedi
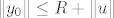
što je kontradikcija jer možemo uzeti y_0 t.d. je
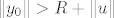 . .
------------------------
Kažem, ovo su precizni i detaljno raspisani dokazi (makar malo zamršeni). Ako je netko zadovoljan sa šlampavim dokazom ili samo s idejom, onda bolje neka se ne muči s ovim mojim cjepidlačenjima. Mislim da nipošto ne treba pamtiti "račun". Zapravo, sad se pitam da li je ovo ikome korisno.  Ali barem je dokaz, a ne "dokaz". Ali barem je dokaz, a ne "dokaz".  Jedino što ovo sad izgleda kao nešto pametno, a zapravo nije. Jedino što ovo sad izgleda kao nešto pametno, a zapravo nije.
|




