| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ane
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 1:58 ned, 7. 5. 2006 Naslov: Postano: 1:58 ned, 7. 5. 2006 Naslov: |
    |
|
|
[u]Ako[/u] mislite na ove zadatke: http://web.math.hr/nastava/unm/zadaci/unm-LU.pdf
[u]onda[/u] su rješenja:
[b]1.[/b] Matrica [latex]A[/latex] dopušta LU-faktorizaciju, budući su joj sve glavne minore različite od 0 i ispadne
[latex]L=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 \\ 2 & -1 & 1 & 0 \\ 1 & 2 & -1 & 1 \end{array} \right ], \quad U=\left [\begin{array}{cccc} 1 & -1 & 0 & 1 \\ 0 & 2 & -1 & 3 \\ 0 & 0 & -1 & 7 \\ 0 & 0 & 0 & 3 \end{array} \right ], \quad x=\left [\begin{array}{c} \frac{4}{3} \\ -\frac{1}{3} \\ -\frac{8}{3} \\ -\frac{2}{3} \end{array} \right ] .[/latex]
[b]2.[/b] Iz teorema s predavanja/vježbi slijedi da ukoliko su sve glavne minore (osim eventualno n-te) matrice [latex]A \in M_n(\mathbb{R})[/latex] različite od 0, tada [latex]A[/latex] dopušta LU-faktorizaciju. Kad te uvjete raspišemo za ovu konkretnu matricu, dobijemo da [latex]A [/latex] svakako dopušta LU faktorizaciju za sve [latex]\lambda \in \mathbb{R} \setminus \{0,2\}[/latex]. Ostaje još provjeriti slučajeve [latex]\lambda =0[/latex] i [latex]\lambda=2[/latex]. No direktnim uvrštavanjem se pokaže da za [latex]\lambda =0[/latex] [latex]A[/latex] dopušta LU-faktorizaciju s
[latex]L=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 \\ 2 & \frac{3}{2} & 1 & 0 \\ 1 & -\frac{5}{4} & \frac{5}{6} & 1 \end{array} \right ], \quad U=\left [\begin{array}{cccc} 2 & 0 & 2 & -1 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & \frac{3}{2} & 3 \\ 0 & 0 & 0 & 2 \end{array} \right ],[/latex]
a za [latex]\lambda=2[/latex] imamo slijedeću situaciju: ona je singularna, a i 3. glavna minora joj je jednaka 0, pa moramo direktnim računom provjeriti da li [latex]A[/latex] dopušta LU-faktorizaciju.
Ako stavimo
[latex]L=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ l_1 & 1 & 0 & 0 \\ l_2 & l_3 & 1 & 0 \\ l_4 & l_5 & l_6 & 1 \end{array} \right ] \quad U=\left [\begin{array}{cccc} u_1 & u_2 & u_3 & u_4 \\ 0 & u_5 & u_6 & u_7 \\ 0 & 0 & u_8 & u_9 \\ 0 & 0 & 0 & u_{10} \end{array} \right ],[/latex]
onda iz jednadžbe
[latex]LU=\left [\begin{array}{cccc} 2 & 0 & 2 & -1 \\ -2 & 2 & -1 & -1 \\ 4 & 2 & 5 & -2 \\ 2 & -4 & 0 & 6\end{array} \right ][/latex]
slijedi da mora biti
[latex]l_1=-1, l_2=2, l_3=1, l_4=1, l_5=-2,[/latex] [latex]u_1=2, u_2=0, u_3=2, u_4=-1, u_5=2, u_6=1, u_7=-2, u_8=0, u_9=2[/latex], dok [latex]l_6[/latex] i [latex]u_{10}[/latex] zadovoljavaju jednadžbu [latex]2l_6+u_{10}=3[/latex]. Dakle i za [latex]\lambda=2[/latex] [latex]A[/latex] dopušta LU-faktorizaciju, i štoviše, imamo neprebrojivo različitih LU-faktorizacija (to ne bi bilo moguće u slučaju da je [latex]A[/latex] regularna).
[b]3.[/b] Dana matrica ne dopušta LU-faktorizaciju, jer joj je već prva glavna minora jednaka 0, a treća glavna minora od [latex]A[/latex] je različita od 0. Koristeći parcijalno pivotiranje dobivamo faktorizaciju [latex]A=PLU[/latex], pri čemu su:
[latex]P=\left [\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{array} \right ], \quad L=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{1}{2} & \frac{1}{2} & -\frac{3}{4} & 1 \end{array} \right ],[/latex]
[latex]U=\left [\begin{array}{cccc} 2 & 2 & 4 & 2 \\ 0 & 2 & 1 & 6 \\ 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & -\frac{7}{2} \end{array} \right ], \quad x=\left [\begin{array}{c} -1 \\ 2 \\ 2 \\ -1 \end{array} \right ]. [/latex]
([latex]x[/latex] je rješenje sustava [latex]Ax=y[/latex]).
[b]4.[/b] dokaz provodimo indukcijom po dimenziji matrice [latex]A \in M_n(\mathbb{R})[/latex] (nije teško).
[b]5.[/b] :D
[u]inače[/u] ne bih znao. :oops:
Ako mislite na ove zadatke: http://web.math.hr/nastava/unm/zadaci/unm-LU.pdf
onda su rješenja:
1. Matrica  dopušta LU-faktorizaciju, budući su joj sve glavne minore različite od 0 i ispadne dopušta LU-faktorizaciju, budući su joj sve glavne minore različite od 0 i ispadne
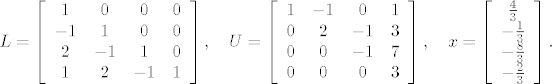
2. Iz teorema s predavanja/vježbi slijedi da ukoliko su sve glavne minore (osim eventualno n-te) matrice 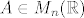 različite od 0, tada različite od 0, tada  dopušta LU-faktorizaciju. Kad te uvjete raspišemo za ovu konkretnu matricu, dobijemo da dopušta LU-faktorizaciju. Kad te uvjete raspišemo za ovu konkretnu matricu, dobijemo da 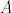 svakako dopušta LU faktorizaciju za sve svakako dopušta LU faktorizaciju za sve 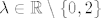 . Ostaje još provjeriti slučajeve . Ostaje još provjeriti slučajeve 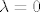 i i 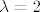 . No direktnim uvrštavanjem se pokaže da za . No direktnim uvrštavanjem se pokaže da za 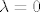  dopušta LU-faktorizaciju s dopušta LU-faktorizaciju s
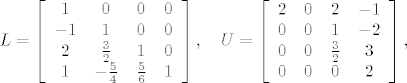
a za 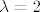 imamo slijedeću situaciju: ona je singularna, a i 3. glavna minora joj je jednaka 0, pa moramo direktnim računom provjeriti da li imamo slijedeću situaciju: ona je singularna, a i 3. glavna minora joj je jednaka 0, pa moramo direktnim računom provjeriti da li  dopušta LU-faktorizaciju. dopušta LU-faktorizaciju.
Ako stavimo

onda iz jednadžbe
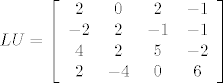
slijedi da mora biti
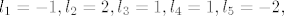 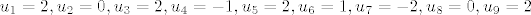 , dok , dok 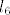 i i 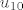 zadovoljavaju jednadžbu zadovoljavaju jednadžbu 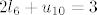 . Dakle i za . Dakle i za 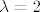  dopušta LU-faktorizaciju, i štoviše, imamo neprebrojivo različitih LU-faktorizacija (to ne bi bilo moguće u slučaju da je dopušta LU-faktorizaciju, i štoviše, imamo neprebrojivo različitih LU-faktorizacija (to ne bi bilo moguće u slučaju da je  regularna). regularna).
3. Dana matrica ne dopušta LU-faktorizaciju, jer joj je već prva glavna minora jednaka 0, a treća glavna minora od  je različita od 0. Koristeći parcijalno pivotiranje dobivamo faktorizaciju je različita od 0. Koristeći parcijalno pivotiranje dobivamo faktorizaciju 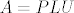 , pri čemu su: , pri čemu su:
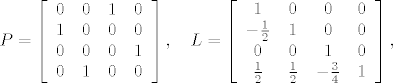

( je rješenje sustava je rješenje sustava 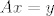 ). ).
4. dokaz provodimo indukcijom po dimenziji matrice 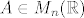 (nije teško). (nije teško).
5. 
inače ne bih znao. 
Zadnja promjena: Ilja; 19:32 pon, 8. 5. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Marko
Forumaš(ica)


Pridružen/a: 16. 06. 2004. (11:05:48)
Postovi: (71)16
Spol: 
|
 Postano: 14:25 pon, 8. 5. 2006 Naslov: Postano: 14:25 pon, 8. 5. 2006 Naslov: |
    |
|
|
Ja sam riješavao taj treći zadatak i dobio sam P, L i U matrice isto ko Ilja. Ali nikako da dobim dobro taj x! Može li mi netko reći gdje griješim, ovako sam to računao:
[latex]Ax=y \Longrightarrow PLUx=y \Longrightarrow Ux=L^{-1}P^{-1}y [/latex]
Gdje je:
[latex]
P^{-1}=\left [\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right ], \quad
L^{-1}=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ \frac{1}{2} & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\frac{1}{2} & -\frac{1}{2} & \frac{3}{4} & 1 \end{array} \right ]
[/latex]
[latex]
y=\left [\begin{array}{cccc} 2 \\ 8 \\ 6 \\ -4 \end{array} \right ] \quad \Longrightarrow P^{-1}y=\left [\begin{array}{cccc} 8 \\ -4 \\ 2 \\ 6 \end{array} \right ]
\Longrightarrow L^{-1}P^{-1}y=\left [\begin{array}{cccc} 8 \\ 0 \\ 2 \\ \frac{15}{2} \end{array} \right ]
[/latex]
E, sad jer je
[latex]
U=\left [\begin{array}{cccc} 2 & 2 & 4 & 2 \\ 0 & 2 & 1 & 6 \\ 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & -\frac{7}{2} \end{array} \right ] [/latex]
dobijem da je [latex]-\frac{7}{2}x_4= \frac{15}{2} \Longrightarrow x_4 = -\frac{15}{7} [/latex]
A treba bi mi x_4 biti -1.
Evo malo sam se raspisao, ali ovo već 2 sata računam i nemogu dobro dobiti! :neznam:
Ja sam riješavao taj treći zadatak i dobio sam P, L i U matrice isto ko Ilja. Ali nikako da dobim dobro taj x! Može li mi netko reći gdje griješim, ovako sam to računao:
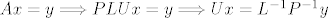
Gdje je:
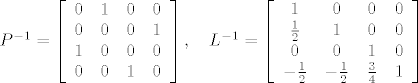
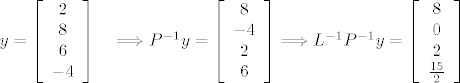
E, sad jer je

dobijem da je 
A treba bi mi x_4 biti -1.
Evo malo sam se raspisao, ali ovo već 2 sata računam i nemogu dobro dobiti! 
_________________
Iljo
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 15:30 pon, 8. 5. 2006 Naslov: Postano: 15:30 pon, 8. 5. 2006 Naslov: |
    |
|
|
Nisi dobro našao inverz [latex]L^{-1}[/latex]. Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od [latex]L[/latex], no to nije inverz od [latex]L[/latex]. Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) [latex]L_i[/latex], ali ne i za traženje inverza njihovog produkta.
Istina je da je za [latex]i<j[/latex] produkt [latex]L_i L_j[/latex] Frobeniusovih matrica [latex]L_i[/latex] i [latex] L_j[/latex] matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od [latex]L_i[/latex], a j-ti stupac od [latex]L_j[/latex].
No Frobeniusove matrice općenito ne komutiraju, tj. [latex]L_i \cdot L_j \neq L_j \ L_i[/latex], pa ako je [latex]L=L_1 \cdots L_{n-1}L_n [/latex] produkt Frobeniusovih matrica [latex]L_i[/latex], onda [latex]L^{-1}=L_n^{-1}L_{n-1}^{-1} \cdots L^{-1}_1[/latex] ne mora biti matrica koja u [latex]i[/latex]-tom stupcu ima [latex]i[/latex]-ti stupac matrice [latex]L^{-1}_{n-i+1}[/latex].
No za rješavanje sustava [latex]LU x=P^{-1}y[/latex] nije potrebno tražiti taj inverz, jer možeš koristiti dobivenu faktorizaciju:
Stavimo [latex]z:=Ux[/latex], rješimo donjetrokutasti sustav [latex]Lz=P^{-1}y[/latex], pa je onda [latex]x[/latex] rješenje gornjetrokutastog sustava [latex]Ux=z[/latex].
Nisi dobro našao inverz 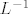 . Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od . Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od  , no to nije inverz od , no to nije inverz od  . Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) . Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) 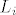 , ali ne i za traženje inverza njihovog produkta. , ali ne i za traženje inverza njihovog produkta.
Istina je da je za 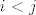 produkt produkt 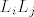 Frobeniusovih matrica Frobeniusovih matrica 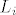 i i 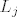 matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od 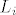 , a j-ti stupac od , a j-ti stupac od 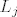 . .
No Frobeniusove matrice općenito ne komutiraju, tj. 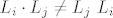 , pa ako je , pa ako je  produkt Frobeniusovih matrica produkt Frobeniusovih matrica 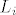 , onda , onda 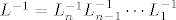 ne mora biti matrica koja u ne mora biti matrica koja u  -tom stupcu ima -tom stupcu ima  -ti stupac matrice -ti stupac matrice 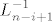 . .
No za rješavanje sustava 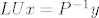 nije potrebno tražiti taj inverz, jer možeš koristiti dobivenu faktorizaciju: nije potrebno tražiti taj inverz, jer možeš koristiti dobivenu faktorizaciju:
Stavimo 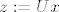 , rješimo donjetrokutasti sustav , rješimo donjetrokutasti sustav 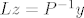 , pa je onda , pa je onda  rješenje gornjetrokutastog sustava rješenje gornjetrokutastog sustava 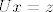 . .
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Ema
Forumaš(ica)

Pridružen/a: 01. 02. 2005. (12:44:59)
Postovi: (9C)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
Bee
Forumaš(ica)
Pridružen/a: 31. 01. 2005. (11:27:34)
Postovi: (91)16
Spol: 
Lokacija: Hicksville
|
|
| [Vrh] |
|
Marko
Forumaš(ica)


Pridružen/a: 16. 06. 2004. (11:05:48)
Postovi: (71)16
Spol: 
|
 Postano: 13:19 uto, 9. 5. 2006 Naslov: Postano: 13:19 uto, 9. 5. 2006 Naslov: |
    |
|
|
[quote="Ilja"]Nisi dobro našao inverz [latex]L^{-1}[/latex]. Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od [latex]L[/latex], no to nije inverz od [latex]L[/latex]. Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) [latex]L_i[/latex], ali ne i za traženje inverza njihovog produkta.
Istina je da je za [latex]i<j[/latex] produkt [latex]L_i L_j[/latex] Frobeniusovih matrica [latex]L_i[/latex] i [latex] L_j[/latex] matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od [latex]L_i[/latex], a j-ti stupac od [latex]L_j[/latex].
No Frobeniusove matrice općenito ne komutiraju, tj. [latex]L_i \cdot L_j \neq L_j \ L_i[/latex], pa ako je [latex]L=L_1 \cdots L_{n-1}L_n [/latex] produkt Frobeniusovih matrica [latex]L_i[/latex], onda [latex]L^{-1}=L_n^{-1}L_{n-1}^{-1} \cdots L^{-1}_1[/latex] ne mora biti matrica koja u [latex]i[/latex]-tom stupcu ima [latex]i[/latex]-ti stupac matrice [latex]L^{-1}_{n-i+1}[/latex].[/quote]
Hvala! :D
Skužio sam to tek kad si ono rekao da mi nije dobar inverz. Pa reko idem onda ja izmnožiti [latex]LL^{-1}[/latex] da vidim... i kad ono... nisam dobio jediničnu matricu.
Evo na kraju taj [latex]L^{-1}[/latex] (koji se sad na kraju uoptšte netreba računati) mi ispadne ovako:
[latex]
L^{-1}=\left [\begin{array}{cccc} 1 & 0 & 0 & 0 \\ \frac{1}{2} & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\frac{3}{4} & -\frac{1}{2} & \frac{3}{4} & 1 \end{array} \right ] [/latex]
I sad sve štima.
[quote="Bee"]Šta je uvijek inverz P matrice njena transponirana matrica?[/quote] E to i mene zanima, jer mi je uvijek do sada ispadalo da je tako.
| Ilja (napisa): | Nisi dobro našao inverz 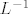 . Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od . Koliko vidim, ti si samo promijenio predznak subdijagonalnim elementima od  , no to nije inverz od , no to nije inverz od  . Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) . Taj način prolazi kod traženja inverza Frobeniusovih matrica (matrica elementarnih transformacija) 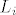 , ali ne i za traženje inverza njihovog produkta. , ali ne i za traženje inverza njihovog produkta.
Istina je da je za 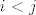 produkt produkt 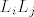 Frobeniusovih matrica Frobeniusovih matrica 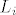 i i 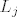 matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od matrica koja na dijagonali ima jedinice, i-ti stupac joj je jednak i-tom stupcu od 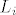 , a j-ti stupac od , a j-ti stupac od 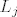 . .
No Frobeniusove matrice općenito ne komutiraju, tj. 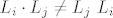 , pa ako je , pa ako je  produkt Frobeniusovih matrica produkt Frobeniusovih matrica 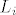 , onda , onda 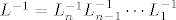 ne mora biti matrica koja u ne mora biti matrica koja u  -tom stupcu ima -tom stupcu ima  -ti stupac matrice -ti stupac matrice 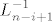 . . |
Hvala! 
Skužio sam to tek kad si ono rekao da mi nije dobar inverz. Pa reko idem onda ja izmnožiti 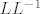 da vidim... i kad ono... nisam dobio jediničnu matricu. da vidim... i kad ono... nisam dobio jediničnu matricu.
Evo na kraju taj 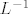 (koji se sad na kraju uoptšte netreba računati) mi ispadne ovako: (koji se sad na kraju uoptšte netreba računati) mi ispadne ovako:
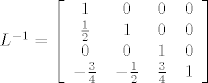
I sad sve štima.
| Bee (napisa): | | Šta je uvijek inverz P matrice njena transponirana matrica? |
E to i mene zanima, jer mi je uvijek do sada ispadalo da je tako.
_________________
Iljo
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 13:32 uto, 9. 5. 2006 Naslov: Postano: 13:32 uto, 9. 5. 2006 Naslov: |
    |
|
|
[quote="Bee"]
Šta je uvijek inverz P matrice njena transponirana matrica?
[/quote]
Aha. Ako vas kojim slučajem zanima i dokaz, čitajte ovo ispod. :P
Ako imamo uređenu bazu [latex](e)=(e_1, \ldots, e_n)[/latex] za [latex]\mathbb{R}^{n}[/latex], permutaciju [latex]\pi \in S_n[/latex] i permutacionu matricu (u bazi [latex](e)[/latex]) [latex]P : e_i \mapsto e_{\pi(i)}[/latex], onda je [latex]P^{\tau}e_{\pi(i)}=e_i[/latex], tj. [latex]P^{\tau}P e_i=e_i[/latex], za sve [latex]1\leq i \leq n[/latex], kao i obrnuto, pa je [latex]P^\tau =P^{-1}[/latex]. Eto. :D
| Bee (napisa): |
Šta je uvijek inverz P matrice njena transponirana matrica?
|
Aha. Ako vas kojim slučajem zanima i dokaz, čitajte ovo ispod. 
Ako imamo uređenu bazu 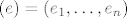 za za 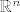 , permutaciju , permutaciju 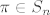 i permutacionu matricu (u bazi i permutacionu matricu (u bazi 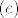 ) ) 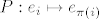 , onda je , onda je 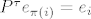 , tj. , tj. 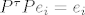 , za sve , za sve 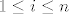 , kao i obrnuto, pa je , kao i obrnuto, pa je 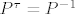 . Eto. . Eto. 
|
|
| [Vrh] |
|
MajaM
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 19:50 uto, 9. 5. 2006 Naslov: Postano: 19:50 uto, 9. 5. 2006 Naslov: |
    |
|
|
[quote="MajaM"]ne kuzim kako u 2. zadatku za lambda=0 dobiti LU faktorizaciju, osim direktnim mnozenjem, isto kao za lambda=2. no, direktnim mnozenjem ne dobivam jedinstvene L i U... thanks[/quote]
Kao što ste rekli: isto direktnim uvrštavanjem. Možda vas je zbunilo to što sam za [latex]\lambda=2[/latex] puno više raspisao nego za [latex]\lambda=0[/latex], a to je zato što sam taj drugi dio naknadno dodado, pa sam tamo i detaljnije raspisao.
Znači, za [latex]\lambda=0[/latex] je ista situacija kao i za [latex]\lambda=2[/latex].
| MajaM (napisa): | | ne kuzim kako u 2. zadatku za lambda=0 dobiti LU faktorizaciju, osim direktnim mnozenjem, isto kao za lambda=2. no, direktnim mnozenjem ne dobivam jedinstvene L i U... thanks |
Kao što ste rekli: isto direktnim uvrštavanjem. Možda vas je zbunilo to što sam za 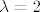 puno više raspisao nego za puno više raspisao nego za 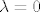 , a to je zato što sam taj drugi dio naknadno dodado, pa sam tamo i detaljnije raspisao. , a to je zato što sam taj drugi dio naknadno dodado, pa sam tamo i detaljnije raspisao.
Znači, za 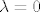 je ista situacija kao i za je ista situacija kao i za 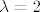 . .
|
|
| [Vrh] |
|
MajaM
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 20:35 uto, 9. 5. 2006 Naslov: Postano: 20:35 uto, 9. 5. 2006 Naslov: |
    |
|
|
A sori. :oops: Tu sam bio odabrao jednu konkretnu LU-faktorizaciju.
Imate pravo, trebao sam sve odmah detaljno raspisati, ali uzmite u obzir vrijeme pisanja onog posta, pa ono. :D
Znači, i za [latex]\lambda=0[/latex] i za [latex]\lambda=2[/latex] imamo neprebrojivo mnogo LU-faktorizacija, a ona koju sam ja gore napisao je samo jedna u moru ostalih. Eto.
A sori.  Tu sam bio odabrao jednu konkretnu LU-faktorizaciju. Tu sam bio odabrao jednu konkretnu LU-faktorizaciju.
Imate pravo, trebao sam sve odmah detaljno raspisati, ali uzmite u obzir vrijeme pisanja onog posta, pa ono. 
Znači, i za 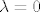 i za i za 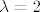 imamo neprebrojivo mnogo LU-faktorizacija, a ona koju sam ja gore napisao je samo jedna u moru ostalih. Eto. imamo neprebrojivo mnogo LU-faktorizacija, a ona koju sam ja gore napisao je samo jedna u moru ostalih. Eto.
|
|
| [Vrh] |
|
gulp
Gost
|
 Postano: 9:59 čet, 11. 5. 2006 Naslov: Postano: 9:59 čet, 11. 5. 2006 Naslov: |
    |
|
|
[quote]...dobijemo da svakako dopušta LU faktorizaciju za sve lambda razlicito od 0 i 2 . Ostaje još provjeriti slučajeve lambda=0,2 . No direktnim uvrštavanjem se pokaže da za lambda=0 dopušta LU-faktorizaciju...[/quote]
[quote]a za lambda=2 imamo slijedeću situaciju:?[b] ona je singularna, a i 3. glavna minora joj je jednaka 0[/b]?, [u]pa moramo direktnim računom provjeriti[/u] da li dopušta LU-faktorizaciju[/quote]
[quote]Dana matrica ne dopušta LU-faktorizaciju, jer joj je već prva glavna minora jednaka 0, ?[u]a treća glavna minora od A je različita od 0[/u]?[/quote]
opcenito, nije mi bas jasno kad trebam provjeriti direktnim uvrstavanjem, kad ne trebam?
| Citat: | | ...dobijemo da svakako dopušta LU faktorizaciju za sve lambda razlicito od 0 i 2 . Ostaje još provjeriti slučajeve lambda=0,2 . No direktnim uvrštavanjem se pokaže da za lambda=0 dopušta LU-faktorizaciju... |
| Citat: | | a za lambda=2 imamo slijedeću situaciju:? ona je singularna, a i 3. glavna minora joj je jednaka 0?, pa moramo direktnim računom provjeriti da li dopušta LU-faktorizaciju |
| Citat: | | Dana matrica ne dopušta LU-faktorizaciju, jer joj je već prva glavna minora jednaka 0, ?a treća glavna minora od A je različita od 0? |
opcenito, nije mi bas jasno kad trebam provjeriti direktnim uvrstavanjem, kad ne trebam?
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
 Postano: 14:08 čet, 11. 5. 2006 Naslov: Postano: 14:08 čet, 11. 5. 2006 Naslov: |
    |
|
|
U vezi 3. zadatka, po mojem racunu matrica permutacije bi trebala biti [{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}], sad ne znam jel sam ja pogrijesio ili Ilja?
U vezi 3. zadatka, po mojem racunu matrica permutacije bi trebala biti [{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}], sad ne znam jel sam ja pogrijesio ili Ilja?
|
|
| [Vrh] |
|
Marko
Forumaš(ica)


Pridružen/a: 16. 06. 2004. (11:05:48)
Postovi: (71)16
Spol: 
|
 Postano: 18:52 čet, 11. 5. 2006 Naslov: Postano: 18:52 čet, 11. 5. 2006 Naslov: |
    |
|
|
[quote="ivo34"]U vezi 3. zadatka, po mojem racunu matrica permutacije bi trebala biti [{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}], sad ne znam jel sam ja pogrijesio ili Ilja?[/quote]
Ta tvoja matrica permutacije P se dobije ako zapisuješ sustav u obliku: LU=PA.
A Iljina matrica P se odnosi na matrični zapis PLU=A.
A zapravo su ti te dvije matrice jedna drugoj inverz. Pročitaj gore početak i vidjet ćeš da sam ja tu tvoju matricu [latex]P[/latex] označio sa [latex]P^{-1}[/latex].
| ivo34 (napisa): | | U vezi 3. zadatka, po mojem racunu matrica permutacije bi trebala biti [{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}], sad ne znam jel sam ja pogrijesio ili Ilja? |
Ta tvoja matrica permutacije P se dobije ako zapisuješ sustav u obliku: LU=PA.
A Iljina matrica P se odnosi na matrični zapis PLU=A.
A zapravo su ti te dvije matrice jedna drugoj inverz. Pročitaj gore početak i vidjet ćeš da sam ja tu tvoju matricu  označio sa označio sa 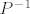 . .
_________________
Iljo
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
|
| [Vrh] |
|
|












