| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
 Postano: 14:24 sri, 27. 9. 2006 Naslov: Postano: 14:24 sri, 27. 9. 2006 Naslov: |
    |
|
|
@Ignavia: Zašto?
@Saf:
[quote]Brojevi kao takvi su ljudska umotvorina[/quote]
Možete li, molim Vas, precizirati. Jeste li konstrukcijom ''kao takvi" željeli izraziti bit pojma broj, ili pojmiti sam pojam broja?
[quote]i stoga su nama ljudima lakše shvatljivi nego jabuke[/quote]
Vjerujem da, ako govorimo o suštini pojma broj, je nemoguće "shvatiti" - odnosno pojmiti broj.
[quote]pa si ja ovo 0.0000... volim predočiti[/quote]
Vjerujem kako si čovjek jedino može predočiti značenje broja, no ne i pojmiti njegovu bit.
@Martinab:
[quote]Apsolutno se slazem s Krckom da je broj 3 lakse shvatiti nego jabuku.[/quote]
Ako ste mislili: "Lakše je predočiti broj 3, nego jabuku", složio bih se, no ako ste mislili: "Lakše je pojmiti broj 3, nego jabuku", želio bih Vas zamoliti, ako ste sposobni i željni, da podjelite svoje znanje samnom i definirate pojam broja.
Molim da moje odgovore ne shvatite kao negativnu provokaciju.
Nemojmo zaboraviti, da bismo definirali pojam potrebno je prvo odrediti rodni pojam, pa specifičnu razliku po kojem se pojam koji definiramo razlikuje od pojmova istog roda.
@Ignavia: Zašto?
@Saf:
| Citat: | | Brojevi kao takvi su ljudska umotvorina |
Možete li, molim Vas, precizirati. Jeste li konstrukcijom ''kao takvi" željeli izraziti bit pojma broj, ili pojmiti sam pojam broja?
| Citat: | | i stoga su nama ljudima lakše shvatljivi nego jabuke |
Vjerujem da, ako govorimo o suštini pojma broj, je nemoguće "shvatiti" - odnosno pojmiti broj.
| Citat: | | pa si ja ovo 0.0000... volim predočiti |
Vjerujem kako si čovjek jedino može predočiti značenje broja, no ne i pojmiti njegovu bit.
@Martinab:
| Citat: | | Apsolutno se slazem s Krckom da je broj 3 lakse shvatiti nego jabuku. |
Ako ste mislili: "Lakše je predočiti broj 3, nego jabuku", složio bih se, no ako ste mislili: "Lakše je pojmiti broj 3, nego jabuku", želio bih Vas zamoliti, ako ste sposobni i željni, da podjelite svoje znanje samnom i definirate pojam broja.
Molim da moje odgovore ne shvatite kao negativnu provokaciju.
Nemojmo zaboraviti, da bismo definirali pojam potrebno je prvo odrediti rodni pojam, pa specifičnu razliku po kojem se pojam koji definiramo razlikuje od pojmova istog roda.
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 15:39 sri, 27. 9. 2006 Naslov: Postano: 15:39 sri, 27. 9. 2006 Naslov: |
    |
|
|
Evo jedne ideje koja potječe od matematičara Johna Hortona Conwaya.
[list]
[*]Svaki broj x je uređen par skupova brojeva L i D pri čemu nijedan broj iz L nije veći ili jednak od nekog broja iz D.
[*]Neka je [latex]x=(X_L,X_D),\ y=(Y_L,Y_D)[/latex]. Tada je [latex]x\leq y[/latex] ako i samo ako ne postoji [latex]x_l\in X_L[/latex] takav da je [latex]y\leq x_l[/latex] i ako ne postoji [latex]y_d\in Y_D[/latex] takav da je [latex]y_d\leq x[/latex].
[/list:u]
Definirajmo [latex]0:=(\emptyset,\emptyset)[/latex]. I dalje lijepo možemo izvesti sve prirodne brojeve, racionalne, iracionalne, pa čak i beskonačno velike i beskonačno male brojeve. :)
Donald E. Knuth je ove brojeve nazvao surealnima, čak je napisao i kratku matematičku novelu o njima (Surreal Numbers). :)
No, što je [latex]\emptyset[/latex]? :-k
Evo jedne ideje koja potječe od matematičara Johna Hortona Conwaya.
- Svaki broj x je uređen par skupova brojeva L i D pri čemu nijedan broj iz L nije veći ili jednak od nekog broja iz D.
- Neka je
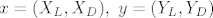 . Tada je . Tada je 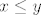 ako i samo ako ne postoji ako i samo ako ne postoji 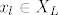 takav da je takav da je 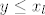 i ako ne postoji i ako ne postoji 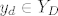 takav da je takav da je 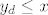 . .
Definirajmo 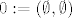 . I dalje lijepo možemo izvesti sve prirodne brojeve, racionalne, iracionalne, pa čak i beskonačno velike i beskonačno male brojeve. . I dalje lijepo možemo izvesti sve prirodne brojeve, racionalne, iracionalne, pa čak i beskonačno velike i beskonačno male brojeve. 
Donald E. Knuth je ove brojeve nazvao surealnima, čak je napisao i kratku matematičku novelu o njima (Surreal Numbers). 
No, što je  ? ? 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
Zadnja promjena: Melkor; 15:43 sri, 27. 9. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 21:19 sri, 27. 9. 2006 Naslov: Postano: 21:19 sri, 27. 9. 2006 Naslov: |
    |
|
|
[quote="Ignavia"][quote="misl4vb"]@Ignavia: Zašto?
[/quote]
zato sto ako to nisi bio ti, onda vas ima vise :faint: :smoke:[/quote]
Mislim da ce ti misl4avb malo teze javiti kolika mu je kratnost kad nije proniknuo u bitak pojma broja :)
[quote="Pericius"][quote="Sir Isaac Newton"]We understand over numbers no as much the set of the units as the abstract ratio of some value to another one of the same kind, which we use as the unit.[/quote]
Dovoljno dobro?
[/quote]
Blaaah, fizicar. Podsjeca me na Sir Francisa Bacona kad je zabrijao da trokuti nisu potpuno plosnati nego da imaju neku debljinu. Moji brojevi postoje neovisno o Njutnovoj potrebi da ih promatra kao omjere. Cak i realni, na koje je stari Isaac vjerojatno ciljao.
[quote="Melkor"]No, što je [latex]\emptyset[/latex]? :-k[/quote]
Sad je stvarno dosta. Ako jos pocnete sumnjat u postojanje praznog skupa, stvarno cu dozivjeti egzistencijalnu krizu. Ja naime vjerujem da cu tamo zavrsiti kad umrem.
:rip: :arrow: [latex]\emptyset[/latex]
| Ignavia (napisa): | | misl4vb (napisa): | @Ignavia: Zašto?
|
zato sto ako to nisi bio ti, onda vas ima vise   |
Mislim da ce ti misl4avb malo teze javiti kolika mu je kratnost kad nije proniknuo u bitak pojma broja 
| Pericius (napisa): | | Sir Isaac Newton (napisa): | | We understand over numbers no as much the set of the units as the abstract ratio of some value to another one of the same kind, which we use as the unit. |
Dovoljno dobro?
|
Blaaah, fizicar. Podsjeca me na Sir Francisa Bacona kad je zabrijao da trokuti nisu potpuno plosnati nego da imaju neku debljinu. Moji brojevi postoje neovisno o Njutnovoj potrebi da ih promatra kao omjere. Cak i realni, na koje je stari Isaac vjerojatno ciljao.
| Melkor (napisa): | No, što je  ? ?  |
Sad je stvarno dosta. Ako jos pocnete sumnjat u postojanje praznog skupa, stvarno cu dozivjeti egzistencijalnu krizu. Ja naime vjerujem da cu tamo zavrsiti kad umrem.
  
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 0:03 čet, 28. 9. 2006 Naslov: Postano: 0:03 čet, 28. 9. 2006 Naslov: |
    |
|
|
[quote="Martinab"]Dakle, Krcko, ako ti netko dokaze da prazan skup ne postoji, zivjet ces zauvijek?[/quote]
Yok. :ccc: Samo ce ga stvoriti kad umre. :D
:rip: :arrow: :creator: :arrow: [latex]\emptyset[/latex]
| Martinab (napisa): | | Dakle, Krcko, ako ti netko dokaze da prazan skup ne postoji, zivjet ces zauvijek? |
Yok.  Samo ce ga stvoriti kad umre. Samo ce ga stvoriti kad umre. 
    
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 10:05 čet, 28. 9. 2006 Naslov: Postano: 10:05 čet, 28. 9. 2006 Naslov: |
    |
|
|
[quote="Martinab"]Dakle, Krcko, ako ti netko dokaze da prazan skup ne postoji, zivjet ces zauvijek?[/quote]
Ja [b]ne zelim[/b] postati zombie :mumija:
To mi je nocna mora jos od osnovnjaka :blueshock:
@misl4vb:
Pojam broja moze se precizno definirati pomocu pojma skupa. Imas dvije razlicite definicije u postovima od Melkora i mdoke. Odgovor na tvoje sljedece pitanje je da se pojam skupa ne definira, nego ga se opisuje aksiomatski.
Da skratimo pricu, najbolje je odmah brojeve uvesti aksiomatski kako se to i radi npr. na kolegiju Matematicka analiza 1. Ti aksiomi su [b]bit[/b] pojma realnog broja i tocno opisuju sto se pod tim misli.
| Martinab (napisa): | | Dakle, Krcko, ako ti netko dokaze da prazan skup ne postoji, zivjet ces zauvijek? |
Ja ne zelim postati zombie 
To mi je nocna mora jos od osnovnjaka 
@misl4vb:
Pojam broja moze se precizno definirati pomocu pojma skupa. Imas dvije razlicite definicije u postovima od Melkora i mdoke. Odgovor na tvoje sljedece pitanje je da se pojam skupa ne definira, nego ga se opisuje aksiomatski.
Da skratimo pricu, najbolje je odmah brojeve uvesti aksiomatski kako se to i radi npr. na kolegiju Matematicka analiza 1. Ti aksiomi su bit pojma realnog broja i tocno opisuju sto se pod tim misli.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 10:10 čet, 28. 9. 2006 Naslov: Postano: 10:10 čet, 28. 9. 2006 Naslov: |
    |
|
|
[b]Dokaz da prazan skup postoji.[/b]
Po definiciji, prazan skup sadrzi sve objekte koji ne postoje. Dakle, kad prazan skup ne bi postojao, bio bi element praznog skupa.
Hmmm, malo prije mi se ucinilo da tu negdje lezi kontradikcija... :-k
Dokaz da prazan skup postoji.
Po definiciji, prazan skup sadrzi sve objekte koji ne postoje. Dakle, kad prazan skup ne bi postojao, bio bi element praznog skupa.
Hmmm, malo prije mi se ucinilo da tu negdje lezi kontradikcija... 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
misl4vb
Forumaš(ica)
Pridružen/a: 24. 09. 2006. (15:35:49)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 20:36 čet, 28. 9. 2006 Naslov: Postano: 20:36 čet, 28. 9. 2006 Naslov: |
    |
|
|
[quote="misl4vb"][quote="krcko"]prazan skup sadrzi sve objekte koji ne postoje[/quote]
:sillyroll:
Analogije citiranoj rečenici:
Torba je puna jabuka koje nisu u torbi.
Zvjezdano je nebo bez zvjezda.
On ima puno toga što nema.[/quote]
Da bi bile analogije, trebo si ovak reć:
Torba sadrži SVE jabuke koje ne postoje (jer ipak postoje jabuke koje nisu u torbi pa ne možeš reći da sadrži sve jabuke koje nisu u torbi, pazi na kvantifikatore)
On ima SVE što ne postoji (ovo što si ti napiso je nemoguće jer skup koji sadrži sve što nije u njemu nije dobro definiran, ne definira svako pravilo skup)
Za drugu rečenicu bi trebo puno napisat, a neda mi se. Pusa, uživaj
| misl4vb (napisa): | | krcko (napisa): | | prazan skup sadrzi sve objekte koji ne postoje |

Analogije citiranoj rečenici:
Torba je puna jabuka koje nisu u torbi.
Zvjezdano je nebo bez zvjezda.
On ima puno toga što nema. |
Da bi bile analogije, trebo si ovak reć:
Torba sadrži SVE jabuke koje ne postoje (jer ipak postoje jabuke koje nisu u torbi pa ne možeš reći da sadrži sve jabuke koje nisu u torbi, pazi na kvantifikatore)
On ima SVE što ne postoji (ovo što si ti napiso je nemoguće jer skup koji sadrži sve što nije u njemu nije dobro definiran, ne definira svako pravilo skup)
Za drugu rečenicu bi trebo puno napisat, a neda mi se. Pusa, uživaj
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 20:49 čet, 28. 9. 2006 Naslov: Postano: 20:49 čet, 28. 9. 2006 Naslov: |
    |
|
|
Buduci da sam se vec jednom "hrvao" s osobom koja je isti ovaj "problem" iznijela, osjecam veliku potrebu da odgovorim na ovaj topic 8)
Problem je u tome sto ti pretpostavljas
[latex]0.\underbrace{0\dots 0}_\infty1 > 0[/latex]
Ali onda po Arhimedovom aksiomu (koji je intuitivno sasvim jasan) postoji neki prirodan broj n takav da je
[latex]n \cdot 0.\underbrace{0\dots 0}_\infty1 > 1 \Longrightarrow n > 10^\infty[/latex]
sto ocito nije moguce, jer je n prirodan broj, pa je to jednako nuli.
(ovdje se pravimo da je beskonacno broj s kojim mozes baratati, ali u principu stvar i je u tome da nije, te ne mozes reci da nakon beskonacno nula ide jedinica jer to nema smisla, buduci da cinjenica da je znamenka k na n-tom mjestu u decimalnom zapisu po definiciji znaci:
[latex]a_0.a_1 \dots a_{n-1} k = a_0.a_1 \dots a_{n-1} + \frac{k}{10^n}[/latex]
no ako je n "beskonacno", onda to jednostavno nema smisla)
Buduci da sam se vec jednom "hrvao" s osobom koja je isti ovaj "problem" iznijela, osjecam veliku potrebu da odgovorim na ovaj topic 
Problem je u tome sto ti pretpostavljas
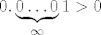
Ali onda po Arhimedovom aksiomu (koji je intuitivno sasvim jasan) postoji neki prirodan broj n takav da je
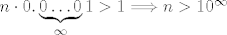
sto ocito nije moguce, jer je n prirodan broj, pa je to jednako nuli.
(ovdje se pravimo da je beskonacno broj s kojim mozes baratati, ali u principu stvar i je u tome da nije, te ne mozes reci da nakon beskonacno nula ide jedinica jer to nema smisla, buduci da cinjenica da je znamenka k na n-tom mjestu u decimalnom zapisu po definiciji znaci:
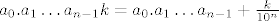
no ako je n "beskonacno", onda to jednostavno nema smisla)
_________________
Bri
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
|
















