| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 22:00 čet, 9. 11. 2006 Naslov: nije od prosle godine, al ipak... Postano: 22:00 čet, 9. 11. 2006 Naslov: nije od prosle godine, al ipak... |
    |
|
|
mislim da nesto rjesenja ima u onoj skripti iz svih predmeta prve godine koja se nalazi u skriptarnici, dodje 200 kn i ima rokove/ispite/kolokvije/i sl. od neke 97,98" do 2000-neke(2003 :roll: moozda, nisam siguran)
odi u skriptarnicu pa si pogledaj
hint: ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova, a i neki su dosta stari.. :wink:
a mozda se tebi svidi 8) go!
mislim da nesto rjesenja ima u onoj skripti iz svih predmeta prve godine koja se nalazi u skriptarnici, dodje 200 kn i ima rokove/ispite/kolokvije/i sl. od neke 97,98" do 2000-neke(2003  moozda, nisam siguran) moozda, nisam siguran)
odi u skriptarnicu pa si pogledaj
hint: ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova, a i neki su dosta stari.. 
a mozda se tebi svidi  go! go!
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 22:24 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... Postano: 22:24 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... |
    |
|
|
[quote="13_mac"]
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova[/quote]
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...).
| 13_mac (napisa): |
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova |
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...).
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
 Postano: 22:37 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... Postano: 22:37 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... |
    |
|
|
[quote="mdoko"][quote="13_mac"]
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova[/quote]
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...).[/quote]
Slazem se, kupila sam i mogu rec da mi i nije bila bas od koristi. Nema novijih kolokvija a neka su do 5-6puta kopirana.
Zato toplo preporucam nase zadace koje su ugl bile teze od kolokvija.
Nemojte se samo ravnat po kolokvijima jer je bio primjedbi na tezinu prijasnjih i onog koji smo mi imali, odnosi se na prvi, pa ne bi bilo lose i ispite proc.
| mdoko (napisa): | | 13_mac (napisa): |
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova |
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...). |
Slazem se, kupila sam i mogu rec da mi i nije bila bas od koristi. Nema novijih kolokvija a neka su do 5-6puta kopirana.
Zato toplo preporucam nase zadace koje su ugl bile teze od kolokvija.
Nemojte se samo ravnat po kolokvijima jer je bio primjedbi na tezinu prijasnjih i onog koji smo mi imali, odnosi se na prvi, pa ne bi bilo lose i ispite proc.
_________________ Kad sam bila mala htjela sam biti statističarka 
[tex]\omega \in \Omega[/tex]  |
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 22:47 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... Postano: 22:47 čet, 9. 11. 2006 Naslov: Re: nije od prosle godine, al ipak... |
    |
|
|
[quote="mdoko"][quote="13_mac"]
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova[/quote]
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...).[/quote]
slazem se :wink:
| mdoko (napisa): | | 13_mac (napisa): |
ja nisam bas prezadovoljan, malo sam iso prelistat i nema previse rijesenih rokova |
IMO, od rijesenih rokova nema bas velike koristi. Korisnije je imati zadatke bez rjesenja i u slucaju da nesto zapne pitati nekoga (kolega, demose, asistente...). |
slazem se 
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
 Postano: 8:19 pet, 10. 11. 2006 Naslov: Postano: 8:19 pet, 10. 11. 2006 Naslov: |
    |
|
|
Rjesenja prve zadace :
1. Df= <-3,-1] U [1,2>
2. f^{-1} ({4,6})= {5,10}
f^{-1} ([2,8>)= [1,17>
3. Nakon pola sata, udaljenost je 7.5km
4. Rf=[3,+oo>
f(<-oo,2]) = [3,+oo>
f^{-1} ([3,5>)=<3-sqrt(5),3>U<3,3+sqrt(5)>
5. Udaljen od A za a/2
Rjesenja prve zadace :
1. Df= ←3,-1] U [1,2>
2. f^{-1} ({4,6})= {5,10}
f^{-1} ([2,8>)= [1,17>
3. Nakon pola sata, udaljenost je 7.5km
4. Rf=[3,+oo>
f(←oo,2]) = [3,+oo>
f^{-1} ([3,5>)=<3-sqrt(5),3>U<3,3+sqrt(5)>
5. Udaljen od A za a/2
_________________ Kad sam bila mala htjela sam biti statističarka 
[tex]\omega \in \Omega[/tex]  |
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 19:18 čet, 23. 11. 2006 Naslov: Postano: 19:18 čet, 23. 11. 2006 Naslov: |
    |
|
|
Ja sam pokušao ovaj:[latex]
f(x)= \frac{5x^{10} +1}{x^{10} +5}[/latex]
Treba odrediti sliku [latex]\mathcal{R}_{f}[/latex] i skup [latex]f^{-1}([1,6])[/latex]
Ja sam to ovako.
Prvo sam podijelio:
[latex]
(5x^{10} +1)[/latex]:[latex](x^{10} +5) = 5[/latex] i ostatak (-24)
Te sam zapisao funkciju na sljedeći način:
[latex]
f(x)=5 - \frac{24}{x^{10} +5}[/latex]
Pa sam je rastavio na 3 kompozicije:
[latex]g_{1}(x) = 5 - x\\
g_{2}(x) = \frac{24}{x+5}\\
g_{3}(x) = x^{10}\\
f = g_{1} \circ g_{2} \circ g_{3}[/latex]
Proučavajući pojedine funkcije zaključio da:
[latex]g_{3}:\mathbb{R} \to [0, +\infty) \\
g_{2}:[0, +\infty)\to (0, \frac{24}{5}]\\
g_{1}:(0, \frac{24}{5}]\to [\frac{1}{5}, 5)
[/latex]
Dakle [latex]\mathcal{R}_{f}=[\frac{1}{5}, 5) [/latex]
Bi li neka dobra (i kompetentna :P) duša ovo malo provjerila. Hvala! :)
Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
Još samo jedno pitanje: za naći inverz u danom intervalu trebao bih riješiti (dvije) nejednadžbe, a bi li mogao jednostavno okrenuti poredak funkcija i upadati iz jedne u drugu (budući da znam grafove - koje sam skicirao prilikom određivanja slike) i sve to skomponirati?
Ja sam pokušao ovaj: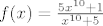
Treba odrediti sliku 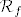 i skup i skup 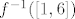
Ja sam to ovako.
Prvo sam podijelio:
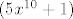 : :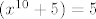 i ostatak (-24) i ostatak (-24)
Te sam zapisao funkciju na sljedeći način:
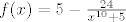
Pa sam je rastavio na 3 kompozicije:
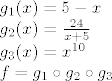
Proučavajući pojedine funkcije zaključio da:
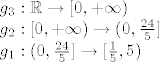
Dakle 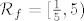
Bi li neka dobra (i kompetentna  ) duša ovo malo provjerila. Hvala! ) duša ovo malo provjerila. Hvala! 
Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
Još samo jedno pitanje: za naći inverz u danom intervalu trebao bih riješiti (dvije) nejednadžbe, a bi li mogao jednostavno okrenuti poredak funkcija i upadati iz jedne u drugu (budući da znam grafove - koje sam skicirao prilikom određivanja slike) i sve to skomponirati?
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 20:10 pet, 24. 11. 2006 Naslov: Postano: 20:10 pet, 24. 11. 2006 Naslov: |
    |
|
|
[quote="Lord R"]Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
Još samo jedno pitanje: za naći inverz u danom intervalu trebao bih riješiti (dvije) nejednadžbe, a bi li mogao jednostavno okrenuti poredak funkcija i upadati iz jedne u drugu (budući da znam grafove - koje sam skicirao prilikom određivanja slike) i sve to skomponirati?[/quote]
Evo, ovako sam dovršio zadatak.
Zapisao kompoziciju na ovajnačin:
[latex]f ^{-1}([1,6])= (g_{1} \circ g_{2} \circ g_{3})^{-1}([1,6])[/latex]
odnosno...
[latex]f ^{-1}([1,6])= (g_{3}^{-1} \circ g_{2}^{-1} \circ g_{1}^{-1})([1,6])[/latex]
Sada nađem kamo se vraćaju pojedine funkcije [i]g[/i] od kompozicije:
[latex]g_{1}^{-1}([1,6]) = [-1,4][/latex]
[latex]g_{2}^{-1}([-1,4]) = [-29,1]\backslash\{0\}[/latex]
[latex]g_{3}^{-1}([-29,1])\backslash \lbrace0\rbrace = [-1,1]\backslash \lbrace0\rbrace[/latex]
Na kraju to još zapišem ovako...
[latex]f ^{-1}([1,6])= [-1,1]\backslash \lbrace0\rbrace[/latex]
Gdje sam pogriješio, što mi ne štima?
| Lord R (napisa): | Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
Još samo jedno pitanje: za naći inverz u danom intervalu trebao bih riješiti (dvije) nejednadžbe, a bi li mogao jednostavno okrenuti poredak funkcija i upadati iz jedne u drugu (budući da znam grafove - koje sam skicirao prilikom određivanja slike) i sve to skomponirati? |
Evo, ovako sam dovršio zadatak.
Zapisao kompoziciju na ovajnačin:
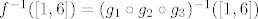
odnosno...
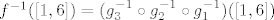
Sada nađem kamo se vraćaju pojedine funkcije g od kompozicije:
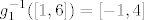

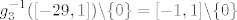
Na kraju to još zapišem ovako...
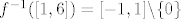
Gdje sam pogriješio, što mi ne štima?
Zadnja promjena: Lord R; 0:03 sub, 25. 11. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vsego
Site Admin

Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:41 pet, 24. 11. 2006 Naslov: Postano: 20:41 pet, 24. 11. 2006 Naslov: |
    |
|
|
Nisam bas raspolozen puno mozgati [ :oops: ], ali ovo mi je zapelo za oko:
[quote="Lord R"][latex]g_{1}([1,6]) = [-1,4][/latex]
[latex]g_{2}([-1,4]) = [-29,1]\backslash\{0\}[/latex]
[latex]g_{3}([-29,1])\backslash \lbrace0\rbrace = [-1,1]\backslash \lbrace0\rbrace[/latex][/quote]
Vjerojatno si htio napisati [latex]g_i^{-1}(\dots)[/latex]. ;)
Vidi ovo: [latex]g_2(-4) = \frac{24}{-4+5} = 24 \not\in [-1,4][/latex] iako je [latex]-4 \in [-29,1] \setminus \{0\}[/latex]. :?
Ne mozes gledati [latex]g_2[/latex] kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije. :( Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u [latex]\pm \infty[/latex]. 8)
Napominjem: ovo sam onako usput primijetio; ne tvrdim da je ista drugo tocno ili krivo. ;)
Nisam bas raspolozen puno mozgati [  ], ali ovo mi je zapelo za oko: ], ali ovo mi je zapelo za oko:
Vjerojatno si htio napisati 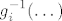 . . 
Vidi ovo: 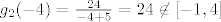 iako je iako je 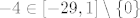 . . 
Ne mozes gledati 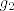 kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije. kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije.  Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u  . . 
Napominjem: ovo sam onako usput primijetio; ne tvrdim da je ista drugo tocno ili krivo. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 20:42 pet, 24. 11. 2006 Naslov: Postano: 20:42 pet, 24. 11. 2006 Naslov: |
    |
|
|
Pokušao sam i ovaj :)
Za funkciju [latex]f:\mathbb{R} \to \[1,3][/latex] definiranu sa:
[latex]f(x) = 9^{\frac{2}{\pi}arcctg(|x-3|+1)}
[/latex]
odredite [latex]f([2, +\infty))[/latex], da li je funkcija surjekcija i skup [latex]f^{-1}(f([2, +\infty]))[/latex].
Prvo sam je rastavio na 3 kompozicije:
[latex]g_{1}(x) = |x-3| + 1\\
g_{2}(x) = 9^{\frac{2}{\pi}arcctg(x)}\\
g_{3}(x) = 9^{x}\\
f(x) = g_{3}(g_{2}(g_{1}(x)))[/latex]
[latex]f([2, +\infty)) = g_{3}(g_{2}(g_{1}([2, +\infty))))[/latex]
Sada za pojedinu funkciju izračunam koje vrijednosti poprima za prethodni izraz
[latex]g_{1}([2, +\infty)) = [1, +\infty)\\
g_{2}([1, +\infty)) = [0, \frac{1}{2})\\
g_{3}([0, \frac{1}{2})) = (1,3][/latex]
Dakle: [latex]f([2, +\infty)) = [2, +\infty)[/latex]
Funkcija nije surjekcija...
Obrazložio bih to ovako...
[latex]f^{-1}(f([2, +\infty\rangle) = f^{-1}(\mathcal{R}_f) = \mathcal{D}_f = \mathbb{R}\\
\mathcal{R}_f = [1,3] \neq \langle 1,3][/latex]
Pokušao sam i ovaj 
Za funkciju 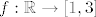 definiranu sa: definiranu sa:
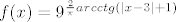
odredite 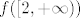 , da li je funkcija surjekcija i skup , da li je funkcija surjekcija i skup 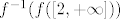 . .
Prvo sam je rastavio na 3 kompozicije:
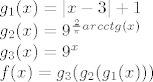
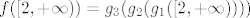
Sada za pojedinu funkciju izračunam koje vrijednosti poprima za prethodni izraz
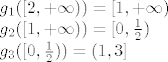
Dakle: 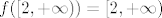
Funkcija nije surjekcija...
Obrazložio bih to ovako...
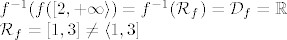
Zadnja promjena: Lord R; 1:21 sub, 25. 11. 2006; ukupno mijenjano 6 put/a.
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 23:56 pet, 24. 11. 2006 Naslov: Postano: 23:56 pet, 24. 11. 2006 Naslov: |
    |
|
|
[quote="vsego"]Nisam bas raspolozen puno mozgati [ :oops: ], ali ovo mi je zapelo za oko:
[quote="Lord R"][latex]g_{1}([1,6]) = [-1,4][/latex]
[latex]g_{2}([-1,4]) = [-29,1]\backslash\{0\}[/latex]
[latex]g_{3}([-29,1])\backslash \lbrace0\rbrace = [-1,1]\backslash \lbrace0\rbrace[/latex][/quote]
Vjerojatno si htio napisati [latex]g_i^{-1}(\dots)[/latex]. ;)
Vidi ovo: [latex]g_2(-4) = \frac{24}{-4+5} = 24 \not\in [-1,4][/latex] iako je [latex]-4 \in [-29,1] \setminus \{0\}[/latex]. :?
Ne mozes gledati [latex]g_2[/latex] kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije. :( Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u [latex]\pm \infty[/latex]. 8)
Napominjem: ovo sam onako usput primijetio; ne tvrdim da je ista drugo tocno ili krivo. ;)[/quote]
Da! Imate pravo, hvala Vam na napomeni i ispravku, pogledat ću još taj zadatak. Popravit ću ono u vezi g^(-1) tako da ne buni. Ako još tko ima nekih ideja, primjedbi ili pokuda ( :( ) rado bi ih čuo...
| vsego (napisa): | Nisam bas raspolozen puno mozgati [  ], ali ovo mi je zapelo za oko: ], ali ovo mi je zapelo za oko:
Vjerojatno si htio napisati 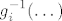 . . 
Vidi ovo: 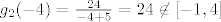 iako je iako je 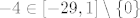 . . 
Ne mozes gledati 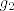 kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije. kao monotonu funkciju (i.e. racunati samo na rubovima) jer ona to nije.  Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u Da nije monotona vidis vec iz cinjenice da je rijec o neprekidnoj funkciji koja prelazi iz negativnih vrijednosti u pozitivne bez da "pogodi" nulu... takve funkciju (u pravilu) u okolici "rupe u domeni" "bjeze" u  . . 
Napominjem: ovo sam onako usput primijetio; ne tvrdim da je ista drugo tocno ili krivo.  |
Da! Imate pravo, hvala Vam na napomeni i ispravku, pogledat ću još taj zadatak. Popravit ću ono u vezi g^(-1) tako da ne buni. Ako još tko ima nekih ideja, primjedbi ili pokuda (  ) rado bi ih čuo... ) rado bi ih čuo...
Zadnja promjena: Lord R; 1:00 sri, 29. 11. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 0:59 sub, 25. 11. 2006 Naslov: Postano: 0:59 sub, 25. 11. 2006 Naslov: |
    |
|
|
Evo još jednog :D...
Funkcija f je zadana formulom:
[latex]f(x)=-log_2(x^4 - 3x^2 +2) [/latex].
Pokažite da je f injekcija na [latex]\langle \sqrt{2}, \sqrt{3}][/latex] i odredite [latex](f|_{\sqrt{2}, \sqrt{3}})[/latex]
Dakle kao i uvijek, razbio sam funkciju na 3 kompozicije:
[latex]g_{1}(x)=x^2\\
g_{2}(x) = x^2 - 3x + 2\\
g_{3}(x)= -log_2x[/latex]
Zatim nacrtao grafove i zaključio:
[latex]g_{1}(\langle \sqrt{2}, \sqrt{3}]) = \langle 2,3][/latex] - injekcija je zato što strogo raste.
[latex]g_{2}(\langle 2,3]) = \langle 0,2][/latex] - injekcija je zato što strogo raste.
[latex]g_{3}(\langle 0,2]) = [-1, \infty \rangle[/latex] - injekcija je zato što je (strogo) monotona.
- f je kompozicija triju injekcija => i sama je injekcija.
Inverz? - Sutra!
Evo još jednog  ... ...
Funkcija f je zadana formulom:
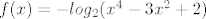 . .
Pokažite da je f injekcija na 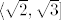 i odredite i odredite 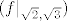
Dakle kao i uvijek, razbio sam funkciju na 3 kompozicije:
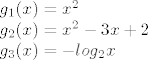
Zatim nacrtao grafove i zaključio:
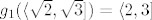 - injekcija je zato što strogo raste. - injekcija je zato što strogo raste.
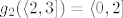 - injekcija je zato što strogo raste. - injekcija je zato što strogo raste.
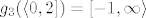 - injekcija je zato što je (strogo) monotona. - injekcija je zato što je (strogo) monotona.
- f je kompozicija triju injekcija ⇒ i sama je injekcija.
Inverz? - Sutra!
Zadnja promjena: Lord R; 1:03 ned, 26. 11. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 14:12 sub, 25. 11. 2006 Naslov: Postano: 14:12 sub, 25. 11. 2006 Naslov: |
    |
|
|
Hehe, hvala (starija) Kolegice :).
Probao sam riješiti jedan s domenom, objavit ću ga pa komentirajte...
[latex]f(x)=log_{9-x^2}\frac{x^2+3x-4}{\sqrt{2^{2x}-2^{x+1}-8}} [/latex]
Dakle, treba odrediti domenu.
Zapisao sam uvjete i riješio svaki od njih:
[size=18][color=red]1. [/color][/size][latex]9-x^2>0[/latex]
odnosno, [latex]x\in\langle -3,3\rangle[/latex]
[color=red][b]2.[/b][/color] [latex]9-x^2\neq 1[/latex]
odnosno, [latex]x\neq\pm \sqrt{8} [/latex]
[color=red][b]3.[/b][/color] [latex]2^{2x}-2{x+1}-8>0[/latex]
kada napravim supstituciju i riješim po suprtituiranoj varijabli imam
[latex]t\in\langle-\infty,-2\rangle \bigcup \langle 4, \infty\rangle [/latex]
Vidim da x ne može biti u prvom intervalu, te zaključim da je
[latex]2^x > 4 /log_2\\
x > 2[/latex]
Logaritmirati smijem, znak nejednakosti ostaje očuvan zato što je logaritam rastuća funkcija.
Za kraj, poslastica :D.
[color=red][b]4.[/b][/color] [latex]\frac{x^2+3x-4}{\sqrt{2^{2x}-2^{x+1}-8}}>0[/latex]
Malo pogledam izraz i uviđam da je nazivnik > 0, dakle još samo treba pogledati kada je brojinik veći od nule - riješim jednadžbu i skiciram si graf, te pročitam:
[latex]x\in\langle-\infty,-4\rangle \bigcup \langle 1, \infty\rangle [/latex]
Sve uvjete nacrtam na jednom pravcu sa jadno označenim (važnim) točkama i gledam gdje se svi preklapaju, a ako sam ja to dobro nacrtao meni ispada ja je:
[latex]\mathcal{D}_f = \langle 2,3 \rangle \backslash \lbrace \sqrt{8}\rbrace[/latex]
Hehe, hvala (starija) Kolegice  . .
Probao sam riješiti jedan s domenom, objavit ću ga pa komentirajte...
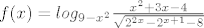
Dakle, treba odrediti domenu.
Zapisao sam uvjete i riješio svaki od njih:
1. 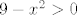
odnosno, 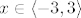
2. 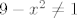
odnosno, 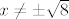
3. 
kada napravim supstituciju i riješim po suprtituiranoj varijabli imam
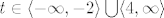
Vidim da x ne može biti u prvom intervalu, te zaključim da je
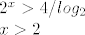
Logaritmirati smijem, znak nejednakosti ostaje očuvan zato što je logaritam rastuća funkcija.
Za kraj, poslastica  . .
4. 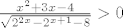
Malo pogledam izraz i uviđam da je nazivnik > 0, dakle još samo treba pogledati kada je brojinik veći od nule - riješim jednadžbu i skiciram si graf, te pročitam:
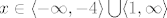
Sve uvjete nacrtam na jednom pravcu sa jadno označenim (važnim) točkama i gledam gdje se svi preklapaju, a ako sam ja to dobro nacrtao meni ispada ja je:
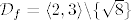
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 15:40 sub, 25. 11. 2006 Naslov: Postano: 15:40 sub, 25. 11. 2006 Naslov: |
    |
|
|
Evo još jednog kojeg sam probao i to ovaj puta iz DZ2.
[latex]f(x)=log_{\frac{1}{3}{|x-3|}}\frac{3^{x-2}-1}{9^{x}-10\cdot 3^{x-1}+1}[/latex]
Kao i u prošlom zadatku ispišem i riješim uvjete te ih na kraju presiječem...
[size=18][color=red]1.[/color][/size]
[latex]\frac{1}{3}|x-3|\neq 1\\
x \neq 6,\\
x \neq 0[/latex]
[size=18][color=red]2.[/color][/size]
[latex]\frac{1}{3}|x-3|> 0\\
\Rightarrow x \in \mathbb{R} \backslash{3}[/latex]
[size=18][color=red]3.[/color][/size]
[latex]{9^{x}-10\cdot 3^{x-1}+1}
3^x = t\\
t_1=3, t_2 = \frac{1}{3}\\
\Rightarrow x\neq 1 \land x \neq -1[/latex]
[size=18][color=red]4.[/color][/size]
[latex]\frac{3^{x-2}-1}{9^{x}-10\cdot 3^{x-1}+1}> 0\\
3^x = t\\
\frac{t-9}{3t^{2}-10t + 3}> 0[/latex]
Znam da je nazivnik manji od nule samo između nultočaka,
[latex]\forall x\in \langle\frac{1}{3},3\rangle \Rightarrow 3t^{2}-10t + 3 > 0 [/latex]
Za brojnik... negativno od minus besk. do 9, ostalo pozitivno.
Dobijem da mi je:
[latex]t\in\langle-\frac{1}{3},3\rangle \bigcup \langle 9, \infty\rangle[/latex]
Za prvi interval:
[latex]- \frac{1}{3}<3^x<3\\
x<1[/latex]
te:
[latex]3^x>9\\
x>2[/latex]
Kada sve to presječem dobijem:
[latex]\mathcal{D}_f = \langle -\infty, 1 \rangle \bigcup \langle 2, +\infty \rangle \backslash{\{-1,0,1,3\} }[/latex]
Evo još jednog kojeg sam probao i to ovaj puta iz DZ2.
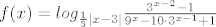
Kao i u prošlom zadatku ispišem i riješim uvjete te ih na kraju presiječem...
1.
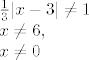
2.
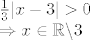
3.
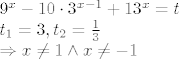
4.
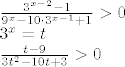
Znam da je nazivnik manji od nule samo između nultočaka,
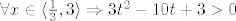
Za brojnik... negativno od minus besk. do 9, ostalo pozitivno.
Dobijem da mi je:
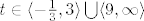
Za prvi interval:
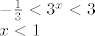
te:
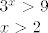
Kada sve to presječem dobijem:
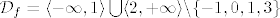
Zadnja promjena: Lord R; 1:04 sri, 29. 11. 2006; ukupno mijenjano 4 put/a.
|
|
| [Vrh] |
|
The Economist
Forumaš(ica)


Pridružen/a: 04. 06. 2006. (00:03:21)
Postovi: (5D)16
Spol: 
|
 Postano: 20:27 sub, 25. 11. 2006 Naslov: Postano: 20:27 sub, 25. 11. 2006 Naslov: |
    |
|
|
[quote="Lord R"][quote="Lord R"]Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
[latex]g_{1}^{-1}([1,6]) = [-1,4][/latex]
[latex]g_{2}^{-1}([-1,4]) = [-29,1]\backslash\{0\}[/latex]
[latex]g_{3}^{-1}([-29,1])\backslash \lbrace0\rbrace = [-1,1]\backslash \lbrace0\rbrace[/latex]
Na kraju to još zapišem ovako...
[latex]f ^{-1}([1,6])= [-1,1]\backslash \lbrace0\rbrace[/latex]
Gdje sam pogriješio, što mi ne štima?[/quote]
Zeznuo si se u drugoj funkciji, naime praslika (to je praslika, a ne inverz) od [-1,4] ti je od (-beskonacno, - 29]U[1, + beskonačno), tj. za te x-eve ti je vrijednost od [-1,4].
E onda ti se gubi ovaj uvjet {0}, sta ti je asist. Sego napisao, i kad to vratis u trecu sliku, izgubis ovaj prvi interval, a za drugi praslika je (-beskonacno, -1]U [1, +beskonacno).
BTW Zivce sam izgubila na tvom oznacavanju funkcija, jao! Valjda funkciju kojom prvom "napadas" zoves g1, a ne obratno ccc.
BTWII Ne moras komponirat 3 funkcije, jednostavno ovo 5-x ubacis kao vertikalnu asimptotu (-5) i zrcalis graf po y-osi.
[quote="Lord R"] | Lord R (napisa): | Za inverz napišem malo kasnije, pisanje u latexu mi puno vremena oduzima...
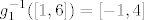

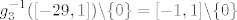
Na kraju to još zapišem ovako...
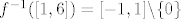
Gdje sam pogriješio, što mi ne štima? |
Zeznuo si se u drugoj funkciji, naime praslika (to je praslika, a ne inverz) od [-1,4] ti je od (-beskonacno, - 29]U[1, + beskonačno), tj. za te x-eve ti je vrijednost od [-1,4].
E onda ti se gubi ovaj uvjet {0}, sta ti je asist. Sego napisao, i kad to vratis u trecu sliku, izgubis ovaj prvi interval, a za drugi praslika je (-beskonacno, -1]U [1, +beskonacno).
BTW Zivce sam izgubila na tvom oznacavanju funkcija, jao! Valjda funkciju kojom prvom "napadas" zoves g1, a ne obratno ccc.
BTWII Ne moras komponirat 3 funkcije, jednostavno ovo 5-x ubacis kao vertikalnu asimptotu (-5) i zrcalis graf po y-osi.
|
|
| [Vrh] |
|
The Economist
Forumaš(ica)


Pridružen/a: 04. 06. 2006. (00:03:21)
Postovi: (5D)16
Spol: 
|
 Postano: 22:00 sub, 25. 11. 2006 Naslov: Postano: 22:00 sub, 25. 11. 2006 Naslov: |
    |
|
|
[quote="Lord R"]Pokušao sam i ovaj :)
Za funkciju [latex]f:\mathbb{R} \to \[1,3][/latex] definiranu sa:
[latex]f(x) = 9^{\frac{2}{\pi}arcctg(|x-3|+1)}
[/latex]
odredite [latex]f([2, +\infty))[/latex], da li je funkcija surjekcija i skup [latex]f^{-1}(f([2, +\infty]))[/latex].
Funkcija nije surjekcija...
Obrazložio bih to ovako...
[latex]f^{-1}(f([2, +\infty\rangle) = f^{-1}(\mathcal{R}_f) = \mathcal{D}_f = \mathbb{R}\\
\mathcal{R}_f = [1,3] \neq \langle 1,3][/latex][/quote]
Ovaj je i meni ovako ispalo, s time da bi ja napisala ovaj zadnji red ovako:
Rf je (1,3] sto je podskup K, dakle nije surjekcija.
Inace svaka cast!
| Lord R (napisa): | Pokušao sam i ovaj 
Za funkciju 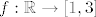 definiranu sa: definiranu sa:
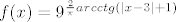
odredite 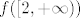 , da li je funkcija surjekcija i skup , da li je funkcija surjekcija i skup 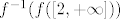 . .
Funkcija nije surjekcija...
Obrazložio bih to ovako...
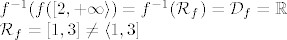 |
Ovaj je i meni ovako ispalo, s time da bi ja napisala ovaj zadnji red ovako:
Rf je (1,3] sto je podskup K, dakle nije surjekcija.
Inace svaka cast!
|
|
| [Vrh] |
|
|






















