| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 16:51 sub, 7. 10. 2006 Naslov: Zadaća Postano: 16:51 sub, 7. 10. 2006 Naslov: Zadaća |
    |
|
|
Evo, bilo je nekih sumnji da li je trebalo pisati sigma-algebra ili samo algebra. Zadatak ipak glasi:
Neka je [latex]A[/latex] familija svih podskupova [latex]B[/latex] na [latex]\textbf{R}[/latex] takvih da je [latex]B[/latex] prebrojiv ili da je [latex]B^C[/latex] prebrojiv. Pokažite da je [latex]A[/latex] sigma-algebra.
Rješenje:
[latex]\emptyset[/latex] je prebrojiv jer je konačan pa je iz [latex]A[/latex].
Uzmimo proizvoljan [latex]B[/latex] iz [latex]A[/latex].
1) [latex]B[/latex] je prebrojiv pa je [latex]\left( {B^C } \right)^C[/latex] prebrojiv, odnosno [latex]B^C[/latex] je iz [latex]A[/latex]
2) [latex]B^C[/latex] je prebrojiv pa je [latex]B[/latex] iz [latex]A[/latex]
Uzmimo proizvoljan niz [latex]B_n[/latex] skupova takvih da [latex]\left( {\forall n \in \textbf{N}} \right)\left( {B_n \in A} \right)[/latex].
1) svi [latex]B_n[/latex] su prebrojivi. Unija prebrojivo mnogo prebrojivih skupova je opet prebrojiv skup ( postoji bijekcija između [latex]\textbf{N}[/latex] i [latex]\textbf{N}\times\textbf{N}[/latex])
2) bar jedan od skupova [latex]B_n[/latex] ima prebrojiv komplement. Tada je [latex]\left( {\bigcup\limits_{n \in {\bf N}} {B_n } } \right)^C = \bigcap\limits_{n \in {\bf N}} {B_n^C }[/latex], a presjek prebrojivog skupa sa proizvoljnim skupom je opet prebrojiv pa je [latex]\bigcup\limits_{n \in {\bf N}} {B_n } \in A[/latex].
Ta-dam. Usput, baš sam ponosan što sad znam pisat ovakve izraze. 8)
Evo, bilo je nekih sumnji da li je trebalo pisati sigma-algebra ili samo algebra. Zadatak ipak glasi:
Neka je  familija svih podskupova familija svih podskupova  na na  takvih da je takvih da je  prebrojiv ili da je prebrojiv ili da je 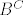 prebrojiv. Pokažite da je prebrojiv. Pokažite da je  sigma-algebra. sigma-algebra.
Rješenje:
 je prebrojiv jer je konačan pa je iz je prebrojiv jer je konačan pa je iz  . .
Uzmimo proizvoljan  iz iz  . .
1)  je prebrojiv pa je je prebrojiv pa je 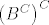 prebrojiv, odnosno prebrojiv, odnosno 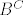 je iz je iz 
2) 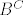 je prebrojiv pa je je prebrojiv pa je  iz iz 
Uzmimo proizvoljan niz 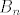 skupova takvih da skupova takvih da 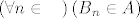 . .
1) svi 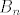 su prebrojivi. Unija prebrojivo mnogo prebrojivih skupova je opet prebrojiv skup ( postoji bijekcija između su prebrojivi. Unija prebrojivo mnogo prebrojivih skupova je opet prebrojiv skup ( postoji bijekcija između  i i  ) )
2) bar jedan od skupova 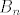 ima prebrojiv komplement. Tada je ima prebrojiv komplement. Tada je 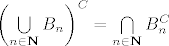 , a presjek prebrojivog skupa sa proizvoljnim skupom je opet prebrojiv pa je , a presjek prebrojivog skupa sa proizvoljnim skupom je opet prebrojiv pa je 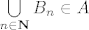 . .
Ta-dam. Usput, baš sam ponosan što sad znam pisat ovakve izraze. 
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
MystiC
Forumaš(ica)

Pridružen/a: 02. 10. 2005. (20:32:44)
Postovi: (CC)16
Spol: 
Lokacija: South of Heaven
|
|
| [Vrh] |
|
Aleksa
Gost
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
alexa
Gost
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
|
| [Vrh] |
|
alexa
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
teh_pwnerer
Forumaš(ica)
Pridružen/a: 02. 02. 2006. (19:06:27)
Postovi: (62)16
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vanja
Forumaš(ica)


Pridružen/a: 16. 02. 2006. (16:38:26)
Postovi: (9E)16
Spol: 
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|











