| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marijana44
Gost
|
|
| [Vrh] |
|
dvičak
Forumaš(ica)


Pridružen/a: 02. 11. 2006. (17:55:13)
Postovi: (60)16
Spol: 
Lokacija: dj-zg
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
Miha Keber
Forumaš(ica)

Pridružen/a: 18. 10. 2006. (20:16:56)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:56 pon, 25. 6. 2007 Naslov: Postano: 16:56 pon, 25. 6. 2007 Naslov: |
    |
|
|
[url=http://degiorgi.math.hr/forum/viewtopic.php?t=9134&start=20]pogledaj tu[/url]
a kad imaš odmah postavljene jednadžbe sa xn i yn onda ide odmah od tog koraka. Ako nešto nije jasno pitaj.
pogledaj tu
a kad imaš odmah postavljene jednadžbe sa xn i yn onda ide odmah od tog koraka. Ako nešto nije jasno pitaj.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
GCOX
Forumaš(ica)

Pridružen/a: 24. 10. 2006. (12:43:03)
Postovi: (A8)16
Spol: 
Lokacija: SPLIT_ZAGREB
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
rhiannon
Forumaš(ica)

Pridružen/a: 11. 06. 2007. (20:34:03)
Postovi: (D)16
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 19:35 pon, 25. 6. 2007 Naslov: Postano: 19:35 pon, 25. 6. 2007 Naslov: |
    |
|
|
[quote="matmih"]Imam i ja pitanje u vezi toga.
Na vježbama smo rješavali zadatak gdje treba naći polinom p tako da vrijedi za svaki p iz P2 f(p)=(p|q). I sada mi smo uvrštavali 1,t i t^2. Međutim to nije ONB. Šta nebi trebalo to prvo ortonormirat i onda krenut sa postupkom, uvrštavanje, integriranje.... :?:[/quote]
Nisam 100% siguran, ali mislim da ne treba miješat dokaz teorema i sam teorem. Naime, zadatak je dobro rješen, jer ako vrijedi za vektore baze, kakva god ona bila, vrijedit će za svaki vektor iz tog prostora. U teoremu je dokazano da je taj vektor jedinstven, prema tome, to mora bit to, neovisno o bazi. Mislim da je u dokazu uzeta o.n.b jer je s njom lakše računat neke stvari (primjerice, odma "znaš" koeficijente linearne kombinacije itd.). Ustvari, trebalo bi provjerit dal je to taj isti vektor koji bi dobio da uzmeš iz dokaza [latex]\sum_{i=1}^n \bar{f(e_{i})}e_{i}[/latex]. Ja sam pre lijen za to, nažalost, možda se nađe neka druga dobra duša. 8)
| matmih (napisa): | Imam i ja pitanje u vezi toga.
Na vježbama smo rješavali zadatak gdje treba naći polinom p tako da vrijedi za svaki p iz P2 f(p)=(p|q). I sada mi smo uvrštavali 1,t i t^2. Međutim to nije ONB. Šta nebi trebalo to prvo ortonormirat i onda krenut sa postupkom, uvrštavanje, integriranje....  |
Nisam 100% siguran, ali mislim da ne treba miješat dokaz teorema i sam teorem. Naime, zadatak je dobro rješen, jer ako vrijedi za vektore baze, kakva god ona bila, vrijedit će za svaki vektor iz tog prostora. U teoremu je dokazano da je taj vektor jedinstven, prema tome, to mora bit to, neovisno o bazi. Mislim da je u dokazu uzeta o.n.b jer je s njom lakše računat neke stvari (primjerice, odma "znaš" koeficijente linearne kombinacije itd.). Ustvari, trebalo bi provjerit dal je to taj isti vektor koji bi dobio da uzmeš iz dokaza 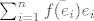 . Ja sam pre lijen za to, nažalost, možda se nađe neka druga dobra duša. . Ja sam pre lijen za to, nažalost, možda se nađe neka druga dobra duša. 
|
|
| [Vrh] |
|
|
















