| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 21:45 pet, 19. 10. 2007 Naslov: Postano: 21:45 pet, 19. 10. 2007 Naslov: |
    |
|
|
Nisam baš siguran je li u redu u cijelosti rješavati zadatke iz službene zadaće na forumu, ali evo hint:
[latex]\frac{(x-1)(x^2-3x+2)^{2006}}{(x^2-7x+12)^{2001}(x-3)}>0[/latex]
Sve što zadatak od tebe zapravo traži je da odrediš x-eve za koje će cijeli razlomak biti [i]strogo veći[/i] od 0.
Dakle, prvi uvjet je da ne smije biti jednak nuli, pa to ne smiju biti niti brojnik niti, naravno, nazivnik.
Drugi uvjet je da, nakon što iz konačnog rješenja eliminiraš sve nultočke, cijeli razlomak mora biti pozitivan. Kada je on strogo pozitivan? Uoči da je izraz u brojniku, [latex](x^2-3x+2)^{2006}[/latex] izraz potenciran parnom potencijom, pa je uvijek pozitivan (i ne smije biti jednak nuli jer to naprosto traži uvjet zadatka pa si nultočke tog polinoma izbacio iz konačnog rješenja).
Potencija u nazivniku, [latex](x^2-7x+12)^{2001}[/latex] je neparna, ali to možeš zapisati kao [latex](x^2-7x+12)^{2000}(x^2-7x+12)[/latex], i naravno, sâme nultočke od [latex]x^2-7x+12[/latex] su isključene.
Kako je nešto na parnu potenciju pozitivno, a u zadatku se traži samo da izračunaš kada će cijeli razlomak biti strogo veći od 0, možeš takve izraze izbaciti iz nejednadžbe, bez da utječeš na konačno rješenje. Tako možeš samo promatrati nejednadžbu [latex]\frac{x-1}{(x^2-7x+12)(x-3)}>0[/latex]
Dalje neću ništa reći, kako ti ne bih pokvario užitak dolaženja do rješenja O:)
Nisam baš siguran je li u redu u cijelosti rješavati zadatke iz službene zadaće na forumu, ali evo hint:
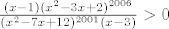
Sve što zadatak od tebe zapravo traži je da odrediš x-eve za koje će cijeli razlomak biti strogo veći od 0.
Dakle, prvi uvjet je da ne smije biti jednak nuli, pa to ne smiju biti niti brojnik niti, naravno, nazivnik.
Drugi uvjet je da, nakon što iz konačnog rješenja eliminiraš sve nultočke, cijeli razlomak mora biti pozitivan. Kada je on strogo pozitivan? Uoči da je izraz u brojniku, 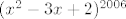 izraz potenciran parnom potencijom, pa je uvijek pozitivan (i ne smije biti jednak nuli jer to naprosto traži uvjet zadatka pa si nultočke tog polinoma izbacio iz konačnog rješenja). izraz potenciran parnom potencijom, pa je uvijek pozitivan (i ne smije biti jednak nuli jer to naprosto traži uvjet zadatka pa si nultočke tog polinoma izbacio iz konačnog rješenja).
Potencija u nazivniku, 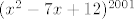 je neparna, ali to možeš zapisati kao je neparna, ali to možeš zapisati kao 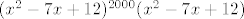 , i naravno, sâme nultočke od , i naravno, sâme nultočke od 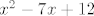 su isključene. su isključene.
Kako je nešto na parnu potenciju pozitivno, a u zadatku se traži samo da izračunaš kada će cijeli razlomak biti strogo veći od 0, možeš takve izraze izbaciti iz nejednadžbe, bez da utječeš na konačno rješenje. Tako možeš samo promatrati nejednadžbu 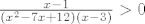
Dalje neću ništa reći, kako ti ne bih pokvario užitak dolaženja do rješenja 
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
anam
Forumaš(ica)

Pridružen/a: 19. 10. 2007. (16:24:34)
Postovi: (B5)16
Lokacija: My Hercegovina!!!!!
|
|
| [Vrh] |
|
|










