| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 12:40 uto, 22. 1. 2008 Naslov: Postano: 12:40 uto, 22. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"]i zar ne treba usporedit sa SIRS?[/quote]
Ne znam, moguće. No ionako je za petak nova zadaća. Profesor se na predavanju u petak zabunio i rekao da je zadaća za petak, a mislio je na ponedjeljak. Ne znam da li se može još predati budući da je zadaća riješena na predavanju, i 1. i 2. zadatak.
Nova zadaća je (za petak):
1. SEIR model, gdje E predstavlja zaražene i zarazne, ali bez simptoma. Za njih je učestalost kontakata [latex]\rho_{E}[/latex], a I predstavlja zarazne sa simptomima, za njih je učestalost kontakata [latex]\rho_{I}[/latex]. Napraviti model.
Običan SEIR model, gdje E predstavlja one koji su zaraženi, ali nisu još zarazni, je dan s
S'=-rSI
E'=rSI - aE
I'=aE-bI
R'=bI
2. (extra) Koja je najčešća spolna bolest?
Profesor je naglasio da se moraju navesti izvori za tvrdnje i da se može promatrati na lokalnoj i globalnoj razini.
[quote]al nejde...crtam SIR model..[/quote]
Vjerojatno zato što trebaš umjesto znaka jednakosti stavljati dvostruko jednako, znači
[code:1]
NDSolve[{S'[x] == -a*S[x]*i[x], i'[x] == a*S[x]*i[x] - b*i[x],
r'[x] == b*i[x], S[0] == 0.999, i[0] == 0.001, r[0] == 0.0},
{S[x], i[x], r[x]}, {x, 0, 30}]
[/code:1]
Obična jednakost se interpretira kao pridruživanje, a dvostruka kao jednakost.
| Luuka (napisa): | | i zar ne treba usporedit sa SIRS? |
Ne znam, moguće. No ionako je za petak nova zadaća. Profesor se na predavanju u petak zabunio i rekao da je zadaća za petak, a mislio je na ponedjeljak. Ne znam da li se može još predati budući da je zadaća riješena na predavanju, i 1. i 2. zadatak.
Nova zadaća je (za petak):
1. SEIR model, gdje E predstavlja zaražene i zarazne, ali bez simptoma. Za njih je učestalost kontakata 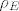 , a I predstavlja zarazne sa simptomima, za njih je učestalost kontakata , a I predstavlja zarazne sa simptomima, za njih je učestalost kontakata 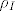 . Napraviti model. . Napraviti model.
Običan SEIR model, gdje E predstavlja one koji su zaraženi, ali nisu još zarazni, je dan s
S'=-rSI
E'=rSI - aE
I'=aE-bI
R'=bI
2. (extra) Koja je najčešća spolna bolest?
Profesor je naglasio da se moraju navesti izvori za tvrdnje i da se može promatrati na lokalnoj i globalnoj razini.
| Citat: | | al nejde...crtam SIR model.. |
Vjerojatno zato što trebaš umjesto znaka jednakosti stavljati dvostruko jednako, znači
| Kod: |
NDSolve[{S'[x] == -a*S[x]*i[x], i'[x] == a*S[x]*i[x] - b*i[x],
r'[x] == b*i[x], S[0] == 0.999, i[0] == 0.001, r[0] == 0.0},
{S[x], i[x], r[x]}, {x, 0, 30}]
|
Obična jednakost se interpretira kao pridruživanje, a dvostruka kao jednakost.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:03 uto, 22. 1. 2008 Naslov: Postano: 22:03 uto, 22. 1. 2008 Naslov: |
    |
|
|
Ja ću probat napravit (jer sam ja mislio da je to za petak) pa ako prođe prođe...a nejde ni ovak...javlja grešku:
[code:1]NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 0.`.[/code:1]
Ja ću probat napravit (jer sam ja mislio da je to za petak) pa ako prođe prođe...a nejde ni ovak...javlja grešku:
| Kod: | | NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 0.`. |
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 1:41 sri, 23. 1. 2008 Naslov: Postano: 1:41 sri, 23. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Ja ću probat napravit (jer sam ja mislio da je to za petak) pa ako prođe prođe...a nejde ni ovak...javlja grešku:
[code:1]NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 0.`.[/code:1][/quote]
Moraš još definirati parametre a i b, tj. uvrstiti konkretne brojeve. Zato ti je dobro napraviti funkciju s argumentima a,b,s0,i0,r0, npr.
[code:1]SIR[a_, r_, s0_, i0_, r0_] :=
(
rj = NDSolve[{S'[x] == -r*i[x]*S[x], P'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*P[x], S[0] == s0, i[0] == i0, R[0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x]/.rj, {x, 0, 30}];
g2 = Plot[i[x]/.rj, {x, 0, 30}];
g3 = Plot[R[x]/.rj, {x, 0, 30}];
)
[/code:1]
Sada lagano dobivaš grafove za varijabilne a i r i konstantne početne uvjete s0, i0 i r0. Možeš još i dvostruku petlju definirati tako da se automatski poziva funkcija za a i r od npr. 0.1, 0.2,... do 1.
| Luuka (napisa): | Ja ću probat napravit (jer sam ja mislio da je to za petak) pa ako prođe prođe...a nejde ni ovak...javlja grešku:
| Kod: | | NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 0.`. |
|
Moraš još definirati parametre a i b, tj. uvrstiti konkretne brojeve. Zato ti je dobro napraviti funkciju s argumentima a,b,s0,i0,r0, npr.
| Kod: | SIR[a_, r_, s0_, i0_, r0_] :=
(
rj = NDSolve[{S'[x] == -r*i[x]*S[x], P'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*P[x], S[0] == s0, i[0] == i0, R[0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x]/.rj, {x, 0, 30}];
g2 = Plot[i[x]/.rj, {x, 0, 30}];
g3 = Plot[R[x]/.rj, {x, 0, 30}];
)
|
Sada lagano dobivaš grafove za varijabilne a i r i konstantne početne uvjete s0, i0 i r0. Možeš još i dvostruku petlju definirati tako da se automatski poziva funkcija za a i r od npr. 0.1, 0.2,... do 1.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:59 sri, 23. 1. 2008 Naslov: Postano: 21:59 sri, 23. 1. 2008 Naslov: |
    |
|
|
Opet ja s problemom. Ne kužim zašto mi nakon definiranja fje onak kak si ti (goranm) napravio naredba
[code:1]SIR[0.1, 0.1, 0.999, 0.001, 0];[/code:1]
ne ispisuje niša osim praznih grafova i brda upozorenja tipa:
[code:1]\NDSolve::"nlnum"The function value {0.0000999`, 1.0000000000000243`*^-7 + P′[0.`], 0.` - 0.1'P[0.`]} is not a list of numbers with dimensions {3} at x = 0.'][/code:1][code:1]Plot::plnr: S[x] /.rj is not a machine-size real number at x= 8.333333333333333`*^-7.[/code:1][code:1]General::stop: Further output of Plot::plnr will be suppressed during this calculation[/code:1]
Opet ja s problemom. Ne kužim zašto mi nakon definiranja fje onak kak si ti (goranm) napravio naredba
| Kod: | | SIR[0.1, 0.1, 0.999, 0.001, 0]; |
ne ispisuje niša osim praznih grafova i brda upozorenja tipa:
| Kod: | | \NDSolve::"nlnum"The function value {0.0000999`, 1.0000000000000243`*^-7 + P′[0.`], 0.` - 0.1'P[0.`]} is not a list of numbers with dimensions {3} at x = 0.'] |
| Kod: | | Plot::plnr: S[x] /.rj is not a machine-size real number at x= 8.333333333333333`*^-7. |
| Kod: | | General::stop: Further output of Plot::plnr will be suppressed during this calculation |
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:44 čet, 24. 1. 2008 Naslov: Postano: 0:44 čet, 24. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Opet ja s problemom.[/quote]
Ja sam krivo copy-pasteao, ispričavam se. Svugdje gdje piše [tt]P[/tt] treba pisati [tt]i[/tt]. Ja sam zaraženu populaciju označavao s P, nisam ih sve u kodu na forumu prepravio u i.
Sada će raditi.
[code:1]SIR[a_, r_, s0_, i0_, r0_] := (
rj = NDSolve[{S'[x] == -r*i[x]*S[x],
i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0},
{S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];
)
[/code:1]
| Luuka (napisa): | | Opet ja s problemom. |
Ja sam krivo copy-pasteao, ispričavam se. Svugdje gdje piše P treba pisati i. Ja sam zaraženu populaciju označavao s P, nisam ih sve u kodu na forumu prepravio u i.
Sada će raditi.
| Kod: | SIR[a_, r_, s0_, i0_, r0_] := (
rj = NDSolve[{S'[x] == -r*i[x]*S[x],
i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0},
{S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];
)
|
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Ivecus
Forumaš(ica)

Pridružen/a: 24. 04. 2006. (18:37:35)
Postovi: (62)16
|
 Postano: 12:01 čet, 24. 1. 2008 Naslov: Postano: 12:01 čet, 24. 1. 2008 Naslov: |
    |
|
|
[code:1]SIR[a_, r_, s0_, i0_, r0_] := (
rj = NDSolve[{S'[x] == -r*i[x]*S[x],
i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0},
{S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];
)
[/code:1]
Meni ovaj kod nece nista iscrtati!? :roll:
| Kod: | SIR[a_, r_, s0_, i0_, r0_] := (
rj = NDSolve[{S'[x] == -r*i[x]*S[x],
i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0},
{S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];
)
|
Meni ovaj kod nece nista iscrtati!? 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3561)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:26 čet, 24. 1. 2008 Naslov: Postano: 12:26 čet, 24. 1. 2008 Naslov: |
    |
|
|
@Ivecus treba ti ovo:
[code:1]SIR[0.1, 0.1, 0.999, 0.001, 0.001];[/code:1]
A kako pobojat graf (kojeg crta Plot) ? I zašto mi kad crtam odvojeno ispada različito od grafa kad crtam skupa? Konkretno imam ovo ( u 2 različita filea):
[code:1]ClearAll[a, r, s0, i0, r0, b, c, d, p0, a0, z0];
SVE[a_, r_, s0_, i0_, r0_, b_, c_, d_, p0_, a0_, z0_] :=
(rj = NDSolve[{S'[x] == -r*i[x]*S[x], i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x], S[0] == s0, i[0] == i0, R[
0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
fj = NDSolve[{P'[x] == d*Z[
x] - c*A[x]*P[x], A'[x] == c*A[x]*P[x] - b*A[x], Z'[x] == b*A[
x] - d*Z[x], P[0] == p0, A[0] == a0, Z[0] == z0}, {P[x],
A[x], Z[x]}, {x, 0, 30}];
f1 = Plot[{S[x] /. rj, P[x] /. fj}, {x, 0, 30}];
f2 = Plot[{i[x] /. rj, A[x] /. fj}, {x, 0, 30}];
f3 = Plot[{R[x] /. rj, Z[x] /. fj}, {x, 0, 30}];)
SVE[0.1, 0.1, 0.999, 0.001, 0.001, 0.1, 0.1, 0.1, 0.999, 0.001, 0.001][/code:1]
[code:1]ClearAll[a, r, s0, i0, r0];
SIR[a_, r_, s0_, i0_, r0_] := (rj = NDSolve[{S'[x] == -r*i[x]*S[x], i'[
x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];)
SIR[0.1, 0.1, 0.999, 0.001, 0.001];
ClearAll[b, c, d, p0, a0, z0];
PAZ[b_, c_, d_, p0_, a0_, z0_] :=
(fja = NDSolve[{P'[x] == d*Z[x] - c*A[x]*P[x], A'[
x] == c*A[x]*P[x] - b*A[x], Z'[x] ==
b*A[x] - d*Z[x], P[0] == p0, A[0] == a0, Z[
0] == z0}, {P[x], A[x], Z[x]}, {x, 0, 30}];
f1 = Plot[P[x] /. fja, {x, 0, 30}];
f2 = Plot[A[x] /. fja, {x, 0, 30}];
f3 = Plot[Z[x] /. fja, {x, 0, 30}];)
PAZ[0.1, 0.1, 0.1, 0.999, 0.001, 0.001][/code:1]
Nazvao sam drugu fju PAZ (da ne bi bilo miješanja koeficijenata)...i sad mi SVE crta različite grafove nego SIR pa PAZ, a trebala bi jedino bit razlika da SVE crta i P i S na istom, a ne odvojeno itd...
@Ivecus treba ti ovo:
| Kod: | | SIR[0.1, 0.1, 0.999, 0.001, 0.001]; |
A kako pobojat graf (kojeg crta Plot) ? I zašto mi kad crtam odvojeno ispada različito od grafa kad crtam skupa? Konkretno imam ovo ( u 2 različita filea):
| Kod: | ClearAll[a, r, s0, i0, r0, b, c, d, p0, a0, z0];
SVE[a_, r_, s0_, i0_, r0_, b_, c_, d_, p0_, a0_, z0_] :=
(rj = NDSolve[{S'[x] == -r*i[x]*S[x], i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x], S[0] == s0, i[0] == i0, R[
0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
fj = NDSolve[{P'[x] == d*Z[
x] - c*A[x]*P[x], A'[x] == c*A[x]*P[x] - b*A[x], Z'[x] == b*A[
x] - d*Z[x], P[0] == p0, A[0] == a0, Z[0] == z0}, {P[x],
A[x], Z[x]}, {x, 0, 30}];
f1 = Plot[{S[x] /. rj, P[x] /. fj}, {x, 0, 30}];
f2 = Plot[{i[x] /. rj, A[x] /. fj}, {x, 0, 30}];
f3 = Plot[{R[x] /. rj, Z[x] /. fj}, {x, 0, 30}];)
SVE[0.1, 0.1, 0.999, 0.001, 0.001, 0.1, 0.1, 0.1, 0.999, 0.001, 0.001] |
| Kod: | ClearAll[a, r, s0, i0, r0];
SIR[a_, r_, s0_, i0_, r0_] := (rj = NDSolve[{S'[x] == -r*i[x]*S[x], i'[
x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x],
S[0] == s0, i[0] == i0, R[0] == r0}, {S[x], i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];)
SIR[0.1, 0.1, 0.999, 0.001, 0.001];
ClearAll[b, c, d, p0, a0, z0];
PAZ[b_, c_, d_, p0_, a0_, z0_] :=
(fja = NDSolve[{P'[x] == d*Z[x] - c*A[x]*P[x], A'[
x] == c*A[x]*P[x] - b*A[x], Z'[x] ==
b*A[x] - d*Z[x], P[0] == p0, A[0] == a0, Z[
0] == z0}, {P[x], A[x], Z[x]}, {x, 0, 30}];
f1 = Plot[P[x] /. fja, {x, 0, 30}];
f2 = Plot[A[x] /. fja, {x, 0, 30}];
f3 = Plot[Z[x] /. fja, {x, 0, 30}];)
PAZ[0.1, 0.1, 0.1, 0.999, 0.001, 0.001] |
Nazvao sam drugu fju PAZ (da ne bi bilo miješanja koeficijenata)...i sad mi SVE crta različite grafove nego SIR pa PAZ, a trebala bi jedino bit razlika da SVE crta i P i S na istom, a ne odvojeno itd...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:39 čet, 24. 1. 2008 Naslov: Postano: 13:39 čet, 24. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"]A kako pobojat graf (kojeg crta Plot)?[/quote]
Ako imaš manje ili jednako od 8 grafova, korisno je koristiti RGBColor unutar Plot funkcije, npr:
[code:1]g1 = Plot[S[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[1,0,0]];
g2 = Plot[i[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,1,0]];
g3 = Plot[R[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,0,1]];[/code:1]
Sada će graf g1 biti obojan crveno, g2 zeleno, a g3 plavo. Mogu se koristiti i kombinacije, npr. RGBColor[1,1,0] što će dati žutu.
Postoji još i CMYKColor[a,b,c,d], gdje su a,b,c i d realni brojevi između 0 i 1.
[quote]I zašto mi kad crtam odvojeno ispada različito od grafa kad crtam skupa? Konkretno imam ovo ( u 2 različita filea):
Nazvao sam drugu fju PAZ (da ne bi bilo miješanja koeficijenata)...i sad mi SVE crta različite grafove nego SIR pa PAZ, a trebala bi jedino bit razlika da SVE crta i P i S na istom, a ne odvojeno itd...[/quote]
Ako sam dobro shvatio (EDIT: nisam shvatio jer nisam dobro pročitao, ali svejedno, korisno je ovo dalje što sam napisao), želiš da se sve tri funkcije u SIR modelu pokažu na jednoj slici? Ako da, onda to možeš ovako napraviti:
U svakoj funkciji obojaj grafove s RGBColorom i dodaj još opciju DisplayFunction->Identity. To će privremeno spriječiti prikazivanje gravfova, a grafove ćeš pozvati ponovo s funkcijom Show. Znači u funkciju ubaci ovo:
[code:1]g1 = Plot[S[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];
g2 = Plot[i[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,1,0],DisplayFunction->Identity];
g3 = Plot[R[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,0,1],DisplayFunction->Identity];
Show[g1,g2,g3, DisplayFunction->$DisplayFunction];
[/code:1]
Naredba DisplayFunction->$DisplayFunction u funkciji Show je bitna jer se inače neće pokazati grafovi (to sve ide unutar funkcije SIR prije nego što zatvoriš zagradu).
Sada kada upišeš npr. SIR[1,0.5,2,1,0] dobiti ćeš jednu sliku na kojoj su sva tri grafa.
[img]http://img521.imageshack.us/img521/2209/grafcy4.jpg[/img]
Korisno ti je postaviti argumente a i r bar iznad 0.5 jer dobivaš jasniju sliku. Stvarni podaci za argument r su od 2 do 10, a za argument a nisam pronašao, vjerojatno je i svejedno jer ovisi o vremenskoj jedinici.
A ako si htio da se S i P pokažu na istoj slici, onda ti treba Show[g1,f1].
| Luuka (napisa): | | A kako pobojat graf (kojeg crta Plot)? |
Ako imaš manje ili jednako od 8 grafova, korisno je koristiti RGBColor unutar Plot funkcije, npr:
| Kod: | g1 = Plot[S[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[1,0,0]];
g2 = Plot[i[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,1,0]];
g3 = Plot[R[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,0,1]]; |
Sada će graf g1 biti obojan crveno, g2 zeleno, a g3 plavo. Mogu se koristiti i kombinacije, npr. RGBColor[1,1,0] što će dati žutu.
Postoji još i CMYKColor[a,b,c,d], gdje su a,b,c i d realni brojevi između 0 i 1.
| Citat: | I zašto mi kad crtam odvojeno ispada različito od grafa kad crtam skupa? Konkretno imam ovo ( u 2 različita filea):
Nazvao sam drugu fju PAZ (da ne bi bilo miješanja koeficijenata)...i sad mi SVE crta različite grafove nego SIR pa PAZ, a trebala bi jedino bit razlika da SVE crta i P i S na istom, a ne odvojeno itd... |
Ako sam dobro shvatio (EDIT: nisam shvatio jer nisam dobro pročitao, ali svejedno, korisno je ovo dalje što sam napisao), želiš da se sve tri funkcije u SIR modelu pokažu na jednoj slici? Ako da, onda to možeš ovako napraviti:
U svakoj funkciji obojaj grafove s RGBColorom i dodaj još opciju DisplayFunction→Identity. To će privremeno spriječiti prikazivanje gravfova, a grafove ćeš pozvati ponovo s funkcijom Show. Znači u funkciju ubaci ovo:
| Kod: | g1 = Plot[S[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];
g2 = Plot[i[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,1,0],DisplayFunction->Identity];
g3 = Plot[R[x] /. rj, {x, 0, 30},PlotStyle->RGBColor[0,0,1],DisplayFunction->Identity];
Show[g1,g2,g3, DisplayFunction->$DisplayFunction];
|
Naredba DisplayFunction→$DisplayFunction u funkciji Show je bitna jer se inače neće pokazati grafovi (to sve ide unutar funkcije SIR prije nego što zatvoriš zagradu).
Sada kada upišeš npr. SIR[1,0.5,2,1,0] dobiti ćeš jednu sliku na kojoj su sva tri grafa.

Korisno ti je postaviti argumente a i r bar iznad 0.5 jer dobivaš jasniju sliku. Stvarni podaci za argument r su od 2 do 10, a za argument a nisam pronašao, vjerojatno je i svejedno jer ovisi o vremenskoj jedinici.
A ako si htio da se S i P pokažu na istoj slici, onda ti treba Show[g1,f1].
_________________
The Dude Abides
Zadnja promjena: goranm; 13:53 čet, 24. 1. 2008; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:45 čet, 24. 1. 2008 Naslov: Postano: 13:45 čet, 24. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"][code:1]ClearAll[a, r, s0, i0, r0, b, c, d, p0, a0, z0];[/code:1][/quote]
Još nešto, nije ti toliko bitno prazniti vrijednost argumentima jer njih svakim pozivom funkcije ionako ponovo inicijaliziraš na novu konstantu. Dovoljno ti je prazniti vrijednosti koje su funkcije S, I i R primile, znači ClearAll[S,i,R] (iako čak niti to nije potrebno jer sa svakim pozivom funkcije rješenja se ponovo interpoliraju).
| Luuka (napisa): | | Kod: | | ClearAll[a, r, s0, i0, r0, b, c, d, p0, a0, z0]; |
|
Još nešto, nije ti toliko bitno prazniti vrijednost argumentima jer njih svakim pozivom funkcije ionako ponovo inicijaliziraš na novu konstantu. Dovoljno ti je prazniti vrijednosti koje su funkcije S, I i R primile, znači ClearAll[S,i,R] (iako čak niti to nije potrebno jer sa svakim pozivom funkcije rješenja se ponovo interpoliraju).
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:14 čet, 24. 1. 2008 Naslov: Postano: 14:14 čet, 24. 1. 2008 Naslov: |
    |
|
|
[quote="Luuka"]A hoću crtat 3 grafa, da usporedim posebno S, posebno I, posebno R fju od svakog modela...al skužio sam princip, smislit ću nešt.[/quote]
Onda koristiš Show[g1,f1];Show[g2,f2];Show[g3,f3];
Možeš si i definirati fiksni okvir da ti skale ne skaču sa jednog omjera na drugi. To radiš s opcijom PlotRange->{{x1,x2},{y1,y2}} unutar funkcije Show, npr.
[code:1]
Show[g1,f1,PlotRange->{{0,30},{0,1}}]
[/code:1]
| Luuka (napisa): | | A hoću crtat 3 grafa, da usporedim posebno S, posebno I, posebno R fju od svakog modela...al skužio sam princip, smislit ću nešt. |
Onda koristiš Show[g1,f1];Show[g2,f2];Show[g3,f3];
Možeš si i definirati fiksni okvir da ti skale ne skaču sa jednog omjera na drugi. To radiš s opcijom PlotRange→{{x1,x2},{y1,y2}} unutar funkcije Show, npr.
| Kod: |
Show[g1,f1,PlotRange->{{0,30},{0,1}}]
|
_________________
The Dude Abides
|
|
| [Vrh] |
|
pucca
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (19:23:02)
Postovi: (1B)16
Lokacija: Osijek
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Ivecus
Forumaš(ica)

Pridružen/a: 24. 04. 2006. (18:37:35)
Postovi: (62)16
|
 Postano: 9:47 pet, 25. 1. 2008 Naslov: Postano: 9:47 pet, 25. 1. 2008 Naslov: |
    |
|
|
Neznam di krivo radim, ali meni grafove nece nacrtati pokraj svih vasih uputa :( , probao sam nesto sam kemijat, pa ne radi onda sam probao copy-pasteat ovo:
[code:1]
ClearAll[a, r, s0, i0, r0];
SIR[a_, r_, s0_, i0_,
r0_] := (rj =
NDSolve[{S'[x] == -r*i[x]*S[x], i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x], S[0] == s0, i[0] == i0, R[0] == r0}, {S[x],
i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];)
SIR[0.1, 0.1, 0.999, 0.001, 0.001]; [/code:1]
pa mi ni to ne radi, a ne baca nikakvu gresku :(
Neznam di krivo radim, ali meni grafove nece nacrtati pokraj svih vasih uputa  , probao sam nesto sam kemijat, pa ne radi onda sam probao copy-pasteat ovo: , probao sam nesto sam kemijat, pa ne radi onda sam probao copy-pasteat ovo:
| Kod: |
ClearAll[a, r, s0, i0, r0];
SIR[a_, r_, s0_, i0_,
r0_] := (rj =
NDSolve[{S'[x] == -r*i[x]*S[x], i'[x] == r*i[x]*S[x] - a*i[x],
R'[x] == a*i[x], S[0] == s0, i[0] == i0, R[0] == r0}, {S[x],
i[x], R[x]}, {x, 0, 30}];
g1 = Plot[S[x] /. rj, {x, 0, 30}];
g2 = Plot[i[x] /. rj, {x, 0, 30}];
g3 = Plot[R[x] /. rj, {x, 0, 30}];)
SIR[0.1, 0.1, 0.999, 0.001, 0.001]; |
pa mi ni to ne radi, a ne baca nikakvu gresku 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 9:53 pet, 25. 1. 2008 Naslov: Postano: 9:53 pet, 25. 1. 2008 Naslov: |
    |
|
|
To bi trebalo radit...al možda nisi sve naredbe izvršio...dakle kod onog clearall shift enter; pa na kraju fje, pa tek onda kod poziva...
[code:1]SIR[1, 0.5, 2, 1, 0][/code:1] a s ovim koeficijentima ljepše izgleda... ;)
To bi trebalo radit...al možda nisi sve naredbe izvršio...dakle kod onog clearall shift enter; pa na kraju fje, pa tek onda kod poziva...
| Kod: | | SIR[1, 0.5, 2, 1, 0] |
a s ovim koeficijentima ljepše izgleda... 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Ivecus
Forumaš(ica)

Pridružen/a: 24. 04. 2006. (18:37:35)
Postovi: (62)16
|
 Postano: 10:03 pet, 25. 1. 2008 Naslov: Postano: 10:03 pet, 25. 1. 2008 Naslov: |
    |
|
|
Evo kako to tocno izgleda u Mathematici
Evo kako to tocno izgleda u Mathematici
| Description: |
|
| Filesize: |
24.41 KB |
| Viewed: |
236 Time(s) |
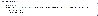
|
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 11:52 pet, 25. 1. 2008 Naslov: Postano: 11:52 pet, 25. 1. 2008 Naslov: |
    |
|
|
[quote="Ivecus"]Neznam di krivo radim, ali meni grafove nece nacrtati pokraj svih vasih uputa...Evo kako to tocno izgleda u Mathematici[/quote]
Ovo je čudno. Možda se radi o nekompatibilnim verzijama? Ja koristim 5.2.
Probaj napraviti
[code:1]
rj=NDSolve[{S'[x] == -0.5*i[x]*S[x], i'[x] == 0.5*i[x]*S[x] - i[x],
R'[x] == i[x], S[0] == 2, i[0] == 1, R[0] == 0}, {S[x], i[x], R[x]}, {x, 0, 30}]
[/code:1]
Nemoj staviti ; na kraju, sada treba izbaciti informaciju o interpoliranju.
Poslije toga onda
[code:1]
Plot[S[x]/.rj,{x,0,30}]
[/code:1]
Ako to neće raditi, onda su ili verzije nekompatibilne ili je došlo do nekakve greške u instalaciji, ne znam :neznam:
| Ivecus (napisa): | | Neznam di krivo radim, ali meni grafove nece nacrtati pokraj svih vasih uputa...Evo kako to tocno izgleda u Mathematici |
Ovo je čudno. Možda se radi o nekompatibilnim verzijama? Ja koristim 5.2.
Probaj napraviti
| Kod: |
rj=NDSolve[{S'[x] == -0.5*i[x]*S[x], i'[x] == 0.5*i[x]*S[x] - i[x],
R'[x] == i[x], S[0] == 2, i[0] == 1, R[0] == 0}, {S[x], i[x], R[x]}, {x, 0, 30}]
|
Nemoj staviti ; na kraju, sada treba izbaciti informaciju o interpoliranju.
Poslije toga onda
| Kod: |
Plot[S[x]/.rj,{x,0,30}]
|
Ako to neće raditi, onda su ili verzije nekompatibilne ili je došlo do nekakve greške u instalaciji, ne znam 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:48 sub, 9. 2. 2008 Naslov: Postano: 14:48 sub, 9. 2. 2008 Naslov: |
    |
|
|
Što očekujemo u 2. kolokviju ?
Ispitivanje stabilnosti ekvilibrija pomoću svojstv vrijednosti matrice, modifikacije SIR modela ili tak nečeg, izvod nekog takvog modela (SIR, SIS, SEIR) ? Što još?
Što očekujemo u 2. kolokviju ?
Ispitivanje stabilnosti ekvilibrija pomoću svojstv vrijednosti matrice, modifikacije SIR modela ili tak nečeg, izvod nekog takvog modela (SIR, SIS, SEIR) ? Što još?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|



















