|
[quote="Meri"]
Tu koristis pretpostavku da je fja f diferencijabilna.
[/quote]
To se lako vidi jer u izrazu stoji funkcija [latex]Df(x)[/latex], dakle diferencijal funkcije f u proizvoljnoj točki(domene), a jamac postojanosti tog diferencijala je pretpostavka da je f diferencijabilna na svojoj domeni.
Dakle, tu, još uvijek stoji nejasnost spomenute transformacije koju Kobra, manje-više :mrgreen:, uspješno rasvjetljuje.
[quote="Kobra"]
Čisto transformirajući definiciju diferencijabilnosti[b]...[/b][/quote]
na IR, zar ne?
Ovdje smo na IR^n.
[quote="Kobra"]
[latex]{f}^{'}(x)=\lim_{\Delta x \rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}[/latex]
Sada uvedeš dvije nove oznake
[latex]
\Delta y = f(x+\Delta x)-f(x)[/latex]
i
[latex]r=\frac{\Delta y}{\Delta x}-{f}^{'}(x)[/latex] a to možemo jer je f diferencijabilna.
Iz ta dva izraza izrazimo f(x + H) - f(x) i dobijamo tvoj zadnji izraz[/quote]
Jesam li dobro shvatio:
[latex]\Delta y = f(x + \Delta x)-f(x)
r = \frac{\Delta y}{\Delta x}-{f}^{'}(x)
r + {f}^{'}(x) = \frac{\Delta y}{\Delta x}
{\Delta x}(r + {f}^{'}(x)) = \Delta y
r\Delta x + {f}^{'}(x)\Delta x = f(x + \Delta x)-f(x)
[/latex]
Uvedem supstituciju [latex]H = \Delta x[/latex]
što je opravdano time da je H u zadatku vektor vrlo "blizak" x-u, baš kao što je [latex]\Delta x[/latex] vrlo blizak x-u u definiciji diferencijabilnosti na IR.
i dobivam:
[latex]f(x + H) - f(x) = r(H) + {f}^{'}(x)(H)[/latex]
S time da nemam derivaciju u točki već diferencijal u točki, a te se funkcije, naravno iz nekog razloga, mogu zamijeniti, a da se ne pokvari jednakost.
Pitam se, zašto je kontekst izraza [latex]f(x + H) - f(x) = r(H) + {f}^{'}(x)(H)[/latex] na vježbama prešućen :?:
Dva su vjerovanja s moje strane:
1. Namjerno prešućivanje poradi poticanja na samostalno kopanje za "velikom istinom".
2. Namjerno izbjegavanje zbog slabe želje za bavljenje dotičnim ili zbog vremenskih tjesnaca.
Ruku na srce, ili, bolje, na mozak, ovo i nije nešto lako dohvatljivo.
Baš me zanima, Kobro, kako si ti došla do tog izraza - konzultacije, znatnije količine LSDa :mrgreen: nešto treće :?:
| Meri (napisa): |
Tu koristis pretpostavku da je fja f diferencijabilna.
|
To se lako vidi jer u izrazu stoji funkcija 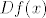 , dakle diferencijal funkcije f u proizvoljnoj točki(domene), a jamac postojanosti tog diferencijala je pretpostavka da je f diferencijabilna na svojoj domeni. , dakle diferencijal funkcije f u proizvoljnoj točki(domene), a jamac postojanosti tog diferencijala je pretpostavka da je f diferencijabilna na svojoj domeni.
Dakle, tu, još uvijek stoji nejasnost spomenute transformacije koju Kobra, manje-više  , uspješno rasvjetljuje. , uspješno rasvjetljuje.
| Kobra (napisa): |
Čisto transformirajući definiciju diferencijabilnosti... |
na IR, zar ne?
Ovdje smo na IR^n.
| Kobra (napisa): |
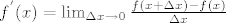
Sada uvedeš dvije nove oznake
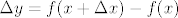
i
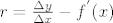 a to možemo jer je f diferencijabilna. a to možemo jer je f diferencijabilna.
Iz ta dva izraza izrazimo f(x + H) - f(x) i dobijamo tvoj zadnji izraz |
Jesam li dobro shvatio:

Uvedem supstituciju 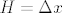
što je opravdano time da je H u zadatku vektor vrlo "blizak" x-u, baš kao što je  vrlo blizak x-u u definiciji diferencijabilnosti na IR. vrlo blizak x-u u definiciji diferencijabilnosti na IR.
i dobivam:

S time da nemam derivaciju u točki već diferencijal u točki, a te se funkcije, naravno iz nekog razloga, mogu zamijeniti, a da se ne pokvari jednakost.
Pitam se, zašto je kontekst izraza  na vježbama prešućen na vježbama prešućen 
Dva su vjerovanja s moje strane:
1. Namjerno prešućivanje poradi poticanja na samostalno kopanje za "velikom istinom".
2. Namjerno izbjegavanje zbog slabe želje za bavljenje dotičnim ili zbog vremenskih tjesnaca.
Ruku na srce, ili, bolje, na mozak, ovo i nije nešto lako dohvatljivo.
Baš me zanima, Kobro, kako si ti došla do tog izraza - konzultacije, znatnije količine LSDa  nešto treće nešto treće 
|








