| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pero
Forumaš(ica)

Pridružen/a: 02. 02. 2005. (17:13:37)
Postovi: (81)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 12:21 ned, 28. 10. 2007 Naslov: Postano: 12:21 ned, 28. 10. 2007 Naslov: |
    |
|
|
Ako se ne varam, Fit traži srednjekvadratnu grešku [latex]\frac{1}{n}\sum_{k=1}^{n} (c e^{\alpha x_k}-y_k)^2[/latex], a kada na izraz [latex]ce^{\alpha x_k} = y_k[/latex] primijeniš ln, onda je
[latex]\ln{y_k} = \ln{c}+\alpha x_k[/latex],
to jest, pravac s koeficijentom smjera [latex]\alpha[/latex] u logaritamskoj skali.
Znači da bi iz dobivenog pravca u logaritamskoj skali trebao očitati koeficijent smjera [latex]\alpha[/latex] (koliko se sjećam, odmah nakon primjene Fit-a se izbaci jednadžba pravca) i onda će funkcija [latex]c e^{\alpha x_k}[/latex] najbolje aproksimirati originalne točke.
Ako se radi o zadaći iz MMUB, manje muke ti je logaritmirati srednjekvadratnu grešku pa tražiti minimum. Svodi se na jednu derivaciju, nekoliko zbrajanja i jedno dijeljenje. :)
Ako se ne varam, Fit traži srednjekvadratnu grešku 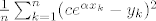 , a kada na izraz , a kada na izraz 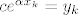 primijeniš ln, onda je primijeniš ln, onda je
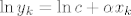 , ,
to jest, pravac s koeficijentom smjera  u logaritamskoj skali. u logaritamskoj skali.
Znači da bi iz dobivenog pravca u logaritamskoj skali trebao očitati koeficijent smjera  (koliko se sjećam, odmah nakon primjene Fit-a se izbaci jednadžba pravca) i onda će funkcija (koliko se sjećam, odmah nakon primjene Fit-a se izbaci jednadžba pravca) i onda će funkcija 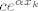 najbolje aproksimirati originalne točke. najbolje aproksimirati originalne točke.
Ako se radi o zadaći iz MMUB, manje muke ti je logaritmirati srednjekvadratnu grešku pa tražiti minimum. Svodi se na jednu derivaciju, nekoliko zbrajanja i jedno dijeljenje. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
pero
Forumaš(ica)

Pridružen/a: 02. 02. 2005. (17:13:37)
Postovi: (81)16
Spol: 
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 10:16 pon, 29. 10. 2007 Naslov: Postano: 10:16 pon, 29. 10. 2007 Naslov: |
    |
|
|
[quote="ivanzub"]jel netkom mozda b ispao negativan? znam da je to nemoguce ali provjeravala sam sto puta i neznam di mi je greska. a mi je 0.029.
formula za b mi ispada
b=suma(lnyi) - a*suma(xi) / n , i=1,..,6
kad uvrstim sve podatke ispada mi negativno!!
jel moze netko napisat koji je postupak za b..
:D[/quote]
Da li ti možda fali kakav ln ispred b? :-k Ako si dobila a, onda ga uvrstiš nazad u bilo koju od parcijalnih derivacija koju si izjednačila s nulom i trebalo bi biti nešto poput [latex]\ln{b}=-c[/latex], gdje je c neki broj koji se već dobije iz računa pa je [latex]b=e^{-c}[/latex] što je pozitivan broj.
Pa onda napišeš jednadžbu i uvrstiš neku od godina i provjeriš da li je rezultat blizu točnim podacima koje imaš.
| ivanzub (napisa): | jel netkom mozda b ispao negativan? znam da je to nemoguce ali provjeravala sam sto puta i neznam di mi je greska. a mi je 0.029.
formula za b mi ispada
b=suma(lnyi) - a*suma(xi) / n , i=1,..,6
kad uvrstim sve podatke ispada mi negativno!!
jel moze netko napisat koji je postupak za b..
 |
Da li ti možda fali kakav ln ispred b?  Ako si dobila a, onda ga uvrstiš nazad u bilo koju od parcijalnih derivacija koju si izjednačila s nulom i trebalo bi biti nešto poput Ako si dobila a, onda ga uvrstiš nazad u bilo koju od parcijalnih derivacija koju si izjednačila s nulom i trebalo bi biti nešto poput 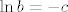 , gdje je c neki broj koji se već dobije iz računa pa je , gdje je c neki broj koji se već dobije iz računa pa je 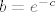 što je pozitivan broj. što je pozitivan broj.
Pa onda napišeš jednadžbu i uvrstiš neku od godina i provjeriš da li je rezultat blizu točnim podacima koje imaš.
_________________
The Dude Abides
|
|
| [Vrh] |
|
|








