| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:58 sub, 9. 2. 2008 Naslov: Postano: 16:58 sub, 9. 2. 2008 Naslov: |
    |
|
|
Ja krenuh sa tim stablima polako i odmah naiđoh na nejasnoću...u attachment stavljam zadatak sa vježbi, prvi primjer kod Kruskala. Tamo smo našli 2 rješenja, al ja nađoh i treće...(pretp da sam dobro prepisao s ploče :) ). Jesu li 2 grafa u 2.redu kao jednaka jer su izomorfni? Gore lijevo je cijeli graf.
Ja krenuh sa tim stablima polako i odmah naiđoh na nejasnoću...u attachment stavljam zadatak sa vježbi, prvi primjer kod Kruskala. Tamo smo našli 2 rješenja, al ja nađoh i treće...(pretp da sam dobro prepisao s ploče  ). Jesu li 2 grafa u 2.redu kao jednaka jer su izomorfni? Gore lijevo je cijeli graf. ). Jesu li 2 grafa u 2.redu kao jednaka jer su izomorfni? Gore lijevo je cijeli graf.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
| Description: |
|
| Filesize: |
22.74 KB |
| Viewed: |
224 Time(s) |

|
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 17:52 sub, 9. 2. 2008 Naslov: Postano: 17:52 sub, 9. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Ne znam da li se kod izomorfnosti spominje težina bridova...samo da je jednak broj vrhova, bridova, čuva se susjedstvo, stupanj vrhova itd. Zbunjen sam... :?[/quote]
pa samo želim reć da mi je glupo govorit o izomorfnosti kad bridove ne gledamo jednako.
ona tvoja dva grafa u dnu iz attachmenta jesu izomorfna, ali ja ih ne bih smatrao jednim rješenjem samo zato što su izomorfni. :? po meni su to dva različita rješenja, jer su drugi bridovi u igri (bridove razlikujemo), a to što je tu slučajno ispalo da su i njihove cijene jednake, to je drugo...
ako uzmeš još i podgraf onog početnog grafa s bridovima {{A,B},{B,E},{B,C},{C,D}}, on jest izomorfan s ona tvoja donja dva, ali upravo zbog drukčije cijene, ne bih rekao da su 'jednaki'.. :roll:
| Luuka (napisa): | Ne znam da li se kod izomorfnosti spominje težina bridova...samo da je jednak broj vrhova, bridova, čuva se susjedstvo, stupanj vrhova itd. Zbunjen sam...  |
pa samo želim reć da mi je glupo govorit o izomorfnosti kad bridove ne gledamo jednako.
ona tvoja dva grafa u dnu iz attachmenta jesu izomorfna, ali ja ih ne bih smatrao jednim rješenjem samo zato što su izomorfni.  po meni su to dva različita rješenja, jer su drugi bridovi u igri (bridove razlikujemo), a to što je tu slučajno ispalo da su i njihove cijene jednake, to je drugo... po meni su to dva različita rješenja, jer su drugi bridovi u igri (bridove razlikujemo), a to što je tu slučajno ispalo da su i njihove cijene jednake, to je drugo...
ako uzmeš još i podgraf onog početnog grafa s bridovima {{A,B},{B,E},{B,C},{C,D}}, on jest izomorfan s ona tvoja donja dva, ali upravo zbog drukčije cijene, ne bih rekao da su 'jednaki'.. 
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:03 sub, 9. 2. 2008 Naslov: Postano: 18:03 sub, 9. 2. 2008 Naslov: |
    |
|
|
Ne bih ni ja rekao da su izomorfni, baš zbog težine bridova, al razlog mojoj zbunjenosti je taj da smo na vježbama našli 2 razapinjujuća stabla s najmanjom težinom, a ja sam našo i treće koristeći isti algoritam...sve 3 su stabla, imaju istu težinu, a različiti su pa si pokušavam objasnit zašt ja imam 3 a Maroje na vježbama našo 2...jel to on fulo ili ja negdje griješim ? :?
Ne bih ni ja rekao da su izomorfni, baš zbog težine bridova, al razlog mojoj zbunjenosti je taj da smo na vježbama našli 2 razapinjujuća stabla s najmanjom težinom, a ja sam našo i treće koristeći isti algoritam...sve 3 su stabla, imaju istu težinu, a različiti su pa si pokušavam objasnit zašt ja imam 3 a Maroje na vježbama našo 2...jel to on fulo ili ja negdje griješim ? 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 18:26 sub, 9. 2. 2008 Naslov: Postano: 18:26 sub, 9. 2. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Ne bih ni ja rekao da su izomorfni, baš zbog težine bridova, al razlog mojoj zbunjenosti je taj da smo na vježbama našli 2 razapinjujuća stabla s najmanjom težinom, a ja sam našo i treće koristeći isti algoritam...sve 3 su stabla, imaju istu težinu, a različiti su pa si pokušavam objasnit zašt ja imam 3 a Maroje na vježbama našo 2...jel to on fulo ili ja negdje griješim ? :?[/quote]
aha. to te muči :) pa kolko sam vidio - to tvoje mi se čini ok. možda maroje nije ni htio ispisati sva rješenja nego samo naglasiti tim primjerom da ih može biti i više od jednog. :vidra:
| Luuka (napisa): | Ne bih ni ja rekao da su izomorfni, baš zbog težine bridova, al razlog mojoj zbunjenosti je taj da smo na vježbama našli 2 razapinjujuća stabla s najmanjom težinom, a ja sam našo i treće koristeći isti algoritam...sve 3 su stabla, imaju istu težinu, a različiti su pa si pokušavam objasnit zašt ja imam 3 a Maroje na vježbama našo 2...jel to on fulo ili ja negdje griješim ?  |
aha. to te muči  pa kolko sam vidio - to tvoje mi se čini ok. možda maroje nije ni htio ispisati sva rješenja nego samo naglasiti tim primjerom da ih može biti i više od jednog. pa kolko sam vidio - to tvoje mi se čini ok. možda maroje nije ni htio ispisati sva rješenja nego samo naglasiti tim primjerom da ih može biti i više od jednog. 
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 13:46 ned, 10. 2. 2008 Naslov: Postano: 13:46 ned, 10. 2. 2008 Naslov: |
    |
|
|
[quote="amorphis"]a što ako imam više bridova iste težine, ali koji nisu međusobno spojeni (npr 1.zd iz zadaće), svaki brid duljine 4 uzimam ponovo (ako ne tvore ciklus) ili kad uzmem jedan 4 onda ih sve iste težine 'eliminiram' dalje?
(možda je glupo pitanje, ali stvarno ne želim ništa pretpostavljat prije kolokvija)[/quote]
Nije bitno jel su ti u tom trenutku povezani. Povezanost je bitna kod Prima. Kruskal uzima brid najmanje težine pazeći da se ne dobije ciklus i to se radi dok graf nije povezan. Prim gleda povezanost u svakom koraku. Bar sam ja to tak skužio
| amorphis (napisa): | a što ako imam više bridova iste težine, ali koji nisu međusobno spojeni (npr 1.zd iz zadaće), svaki brid duljine 4 uzimam ponovo (ako ne tvore ciklus) ili kad uzmem jedan 4 onda ih sve iste težine 'eliminiram' dalje?
(možda je glupo pitanje, ali stvarno ne želim ništa pretpostavljat prije kolokvija) |
Nije bitno jel su ti u tom trenutku povezani. Povezanost je bitna kod Prima. Kruskal uzima brid najmanje težine pazeći da se ne dobije ciklus i to se radi dok graf nije povezan. Prim gleda povezanost u svakom koraku. Bar sam ja to tak skužio
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 12:22 pon, 11. 2. 2008 Naslov: Postano: 12:22 pon, 11. 2. 2008 Naslov: |
    |
|
|
Da ne otvaram novu temu... Imam pitanje u vezi 2 zadatka sa vježbi.
1. Koliko ima svih mulitgrafova čiji je skup vrhova [latex]V=\{v_1, v_2,..., v_n\}[/latex], a svi imaju točno m bridova.
Rj: dvočlanih multiskupova skupa [latex]V=\{v_1, v_2,..., v_n\}[/latex] ima [latex] \left( \begin{array}{cc}n+1 \\ 2 \\ \end{array} \right)[/latex]
Svaki brid mozemo prodruziti multiskupu.
[latex]x_1+x_2+...+x_{\left( \begin{array}{cc}n+1 \\ 2 \\ \end{array} \right)}=m, x_i\geq0[/latex]
Dobivamo (n+1 povrh 2 + m -1) povrh m (ne ide mi bas latex danas pa pisem dalje ovak, sorry :))
Ne kuzim zasto gledamo dvoclane multiskupove, i zasto ih ima bas toliko. Jasno mi je da je ovo n kraju samo br rjesenja jednadzebe, ali kako uopce dodjemo do nje? :?
2. Pokazite da jednostavan graf s p vrhova, gdje svi vrhovi imaju stupanj >=1/2*(p-1) mora biti povezan.
Rj: Pretp suprorno: postoji nepovezan graf sa ovim svojstvom
neka su [latex]v_1, v_2,...,v_n[/latex] komponetne povezanosti
postoji [latex]v_i[/latex] t.d. je broj vrhova od [latex]v_i\leq \lfloor \frac{p}{2}\rfloor[/latex]
Uzmimo vrh x iz [latex]v_i[/latex], [latex]d(x)\geq\frac{1}{2}(p-1)[/latex]
Ukupno vrhova u [latex]v_i[/latex] ima [latex]\leq \lfloor \frac{p}{2}\rfloor[/latex]
[latex] \frac{1}{2}(p-1)\geq\lfloor \frac{p}{2}\rfloor-1\geq d(x)[/latex]
[latex]\frac{1}{2}p-\frac{1}{2}\geq\lfloor \frac{p}{2}\rfloor-1[/latex]
Uopce ne kuzim sto smo mi tu dokazivali ni kako pa ako mi netko moze objasniti zasto to ovako ide....
Tnx :)
Da ne otvaram novu temu... Imam pitanje u vezi 2 zadatka sa vježbi.
1. Koliko ima svih mulitgrafova čiji je skup vrhova 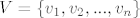 , a svi imaju točno m bridova. , a svi imaju točno m bridova.
Rj: dvočlanih multiskupova skupa 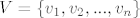 ima ima 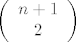
Svaki brid mozemo prodruziti multiskupu.
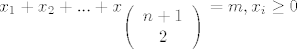
Dobivamo (n+1 povrh 2 + m -1) povrh m (ne ide mi bas latex danas pa pisem dalje ovak, sorry  ) )
Ne kuzim zasto gledamo dvoclane multiskupove, i zasto ih ima bas toliko. Jasno mi je da je ovo n kraju samo br rjesenja jednadzebe, ali kako uopce dodjemo do nje? 
2. Pokazite da jednostavan graf s p vrhova, gdje svi vrhovi imaju stupanj >=1/2*(p-1) mora biti povezan.
Rj: Pretp suprorno: postoji nepovezan graf sa ovim svojstvom
neka su 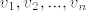 komponetne povezanosti komponetne povezanosti
postoji 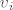 t.d. je broj vrhova od t.d. je broj vrhova od 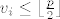
Uzmimo vrh x iz 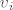 , , 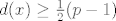
Ukupno vrhova u 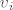 ima ima 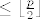
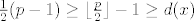
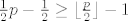
Uopce ne kuzim sto smo mi tu dokazivali ni kako pa ako mi netko moze objasniti zasto to ovako ide....
Tnx 
_________________  |
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
 Postano: 14:52 pon, 11. 2. 2008 Naslov: Postano: 14:52 pon, 11. 2. 2008 Naslov: |
    |
|
|
Maroje je definirao multiskup M kao M={V,E}={n,m} (jer je u grafu n vrhova i m bridova) , dozvolio je petlje i višestruko ponavljanje bridova u grafu nakon čega je prebrojavao koliko bridova različite vrste postoji; bridova ima (n povrh 2) komada (jer svaki brid 'radi' sa 2 vrha), petlji ima (n povrh 1) komada (jer svaka petlja 'radi' samo sa jednim vrhom) što kad se sumira daje kao ukupan broj bridova upravo ((n+1) povrh 2), nakon toga Maroje tvrdi da je x1=broj brodova 1. vrste (npr petlje), x2=br. bridova 2. vrste (npr višestruki bridovi) odnosno xi=br. bridova i-te vrste i kad ih sumira (x1+x2+...+xi) mora ih biti točno m (jer je to uvijet zadatka), a to se onda riješi isto kao i zd. tipa 'koliko ima cijelobrojnih rješenja jdžbe' (imaš sličan zd na vježbama od 31.10.2007.) i (dobiješ (m+(n+1 povrh 2)-1)povrh m)
Maroje je definirao multiskup M kao M={V,E}={n,m} (jer je u grafu n vrhova i m bridova) , dozvolio je petlje i višestruko ponavljanje bridova u grafu nakon čega je prebrojavao koliko bridova različite vrste postoji; bridova ima (n povrh 2) komada (jer svaki brid 'radi' sa 2 vrha), petlji ima (n povrh 1) komada (jer svaka petlja 'radi' samo sa jednim vrhom) što kad se sumira daje kao ukupan broj bridova upravo ((n+1) povrh 2), nakon toga Maroje tvrdi da je x1=broj brodova 1. vrste (npr petlje), x2=br. bridova 2. vrste (npr višestruki bridovi) odnosno xi=br. bridova i-te vrste i kad ih sumira (x1+x2+...+xi) mora ih biti točno m (jer je to uvijet zadatka), a to se onda riješi isto kao i zd. tipa 'koliko ima cijelobrojnih rješenja jdžbe' (imaš sličan zd na vježbama od 31.10.2007.) i (dobiješ (m+(n+1 povrh 2)-1)povrh m)
|
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
 Postano: 15:27 pon, 11. 2. 2008 Naslov: Postano: 15:27 pon, 11. 2. 2008 Naslov: |
    |
|
|
za drugi zadatak;
pretpostavi se suprotno, tj. postoji graf sa zadanim svojstvom, ali koji nije povezan, ako nije povezan znači da postoje komponente povezanosti (v1, v2, ..., vn) i među njima mora biti barem jedna čiji je broj vrhova manji od (ili jednak) 'najmanjem cijelom od P/2' jer ako bi sve komponente imale više od toliko vrhova onda bi i ukupna suma vrhova bila veća od P, a što ne smije biti zbog uvjeta zadatka, neka je dalje stupanj (proizvoljnog) vrha x>=(P-1)/2, neka je taj x iz komponente v1, jer je |v1|<=P/2 znači da x smije imati najviše 'najmanje cijelo od P/2' susjeda što znači da je 'najmanje cijelo od (P/2)' - 1<=(P-1)/2 što je kontradikcija s uvjetom zadatka i vrijedi da graf zbilja mora biti povezan
za drugi zadatak;
pretpostavi se suprotno, tj. postoji graf sa zadanim svojstvom, ali koji nije povezan, ako nije povezan znači da postoje komponente povezanosti (v1, v2, ..., vn) i među njima mora biti barem jedna čiji je broj vrhova manji od (ili jednak) 'najmanjem cijelom od P/2' jer ako bi sve komponente imale više od toliko vrhova onda bi i ukupna suma vrhova bila veća od P, a što ne smije biti zbog uvjeta zadatka, neka je dalje stupanj (proizvoljnog) vrha x>=(P-1)/2, neka je taj x iz komponente v1, jer je |v1|<=P/2 znači da x smije imati najviše 'najmanje cijelo od P/2' susjeda što znači da je 'najmanje cijelo od (P/2)' - 1<=(P-1)/2 što je kontradikcija s uvjetom zadatka i vrijedi da graf zbilja mora biti povezan
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
buzov5
Forumaš(ica)

Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
|



















