| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
 Postano: 8:53 sri, 3. 9. 2008 Naslov: Par zadataka sa vježbi Postano: 8:53 sri, 3. 9. 2008 Naslov: Par zadataka sa vježbi |
    |
|
|
Evo učim već neko vrijeme, mislila sam da će s vremenom i radom neke nejasnoće postati jasne, ali ne ide.... :cry:
1. Neka je A skup i X neprazan podskup od A. Dokazite da postoji relacija ekvivalencije ~ na A t.d. svaka klasa ekvivalencije ima točno jednog reprezentanta u X.
Rj. Želimo da je {A1, A2, A3....} particija od A i Ai presjek X={x}.
X je neprazan. uzmemo da je x0 element od X.
promatramo {x0}UA\X=A1. (do ovdje kužim)
def. za xeX\{x0} skup Ax={x} (zašto, čemu to služi?)
def. za a,beA a~b <=>a,be{xo}U(A\X) ili a=b.
Ova zadnja 2 reda ne razumijem šta je pjesnik htio reći. Zašto sad uzimamo a i b isključivo iz ovog skupa, čemu nam uopće služi ovaj Ax?
2.Odredite kardinalnost skupa svih podskupova od R koji su ekvipotentni s R.
To smo trebali sami riješiti za zadaću, ali ne znam izmisliti funkciju. Kad vidim neki riješen zadatak kužim zašto baš ta funkcija, ali sama uopće ne znam odakle bi krenula.
(Razumijem onaj dio gdje postavio da je X={A podskup od R: A~R}. To je poskup partitivnog skupa i imamo k(X)<=2^c. Ne razumijem onu drugu stranu koja nije ovako trivijalna. :))
Hvala
Evo učim već neko vrijeme, mislila sam da će s vremenom i radom neke nejasnoće postati jasne, ali ne ide.... 
1. Neka je A skup i X neprazan podskup od A. Dokazite da postoji relacija ekvivalencije ~ na A t.d. svaka klasa ekvivalencije ima točno jednog reprezentanta u X.
Rj. Želimo da je {A1, A2, A3....} particija od A i Ai presjek X={x}.
X je neprazan. uzmemo da je x0 element od X.
promatramo {x0}UA\X=A1. (do ovdje kužim)
def. za xeX\{x0} skup Ax={x} (zašto, čemu to služi?)
def. za a,beA a~b <=>a,be{xo}U(A\X) ili a=b.
Ova zadnja 2 reda ne razumijem šta je pjesnik htio reći. Zašto sad uzimamo a i b isključivo iz ovog skupa, čemu nam uopće služi ovaj Ax?
2.Odredite kardinalnost skupa svih podskupova od R koji su ekvipotentni s R.
To smo trebali sami riješiti za zadaću, ali ne znam izmisliti funkciju. Kad vidim neki riješen zadatak kužim zašto baš ta funkcija, ali sama uopće ne znam odakle bi krenula.
(Razumijem onaj dio gdje postavio da je X={A podskup od R: A~R}. To je poskup partitivnog skupa i imamo k(X)<=2^c. Ne razumijem onu drugu stranu koja nije ovako trivijalna.  ) )
Hvala
_________________  |
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 12:45 čet, 4. 9. 2008 Naslov: Postano: 12:45 čet, 4. 9. 2008 Naslov: |
    |
|
|
@Mad Wilson: Ne znam točno kakav hint želiš. Trebao si napisati na kojem smjeru dokazivanja ekvivalencije si zapeo.
Kako se meni čini, najproblematičnije je uz pretpostavku [latex]R_1\cup R_2=R_2\circ R_1[/latex] dobiti tranzitivnost relacije [latex]R_1\cup R_2[/latex].
No, pretpostavi [latex]x\mathbin{(R_1\cup R_2)} z[/latex] i [latex]z\mathbin{(R_1\cup R_2)} y[/latex]. Tad imaš četiri mogućnosti.
Ako je [latex]x\mathbin{R_1}z[/latex] i [latex]z\mathbin{R_1} y[/latex], onda zbog tranzitivnosti relacije [latex]R_1[/latex] vrijedi [latex]x\mathbin{R_1}y[/latex] pa i [latex]x\mathbin{(R_1\cup R_2)} y[/latex]. Analogno u slučaju [latex]x\mathbin{R_2}z[/latex] i [latex]z\mathbin{R_2} y[/latex].
Ako je [latex]x\mathbin{R_1}z[/latex] i [latex]z\mathbin{R_2} y[/latex], onda je [latex]x\mathbin{(R_2\circ R_1)} y[/latex] pa iz [latex]R_1\cup R_2=R_2\circ R_1[/latex] slijedi [latex]x\mathbin{(R_1\cup R_2)} y[/latex].
Konačno, ako je [latex]x\mathbin{R_2}z[/latex] i [latex]z\mathbin{R_1} y[/latex], zbog simetričnosti relacija [latex]R_1[/latex] i [latex]R_2[/latex] imamo [latex]z\mathbin{R_2}x[/latex] i [latex]y\mathbin{R_1} z[/latex]. Slijedi da je [latex]y\mathbin{(R_2\circ R_1)} x[/latex], tj. slično kao u prošlom slučaju, [latex]y\mathbin{(R_1\cup R_2)} x[/latex]. Ali simetričnost [latex]R_1\cup R_2[/latex] je evidentna jer su obje relacije [latex]R_1[/latex] i [latex]R_2[/latex] simetrične.
Dakle, u svakom slučaju iz pretpostavke [latex]x\mathbin{(R_1\cup R_2)} z[/latex] i [latex]z\mathbin{(R_1\cup R_2)} y[/latex] slijedi [latex]x\mathbin{(R_1\cup R_2)} y[/latex] pa je to tranzitivna relacija.
@Mad Wilson: Ne znam točno kakav hint želiš. Trebao si napisati na kojem smjeru dokazivanja ekvivalencije si zapeo.
Kako se meni čini, najproblematičnije je uz pretpostavku 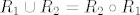 dobiti tranzitivnost relacije dobiti tranzitivnost relacije 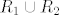 . .
No, pretpostavi 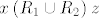 i i 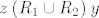 . Tad imaš četiri mogućnosti. . Tad imaš četiri mogućnosti.
Ako je 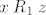 i i 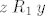 , onda zbog tranzitivnosti relacije , onda zbog tranzitivnosti relacije 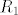 vrijedi vrijedi 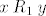 pa i pa i 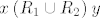 . Analogno u slučaju . Analogno u slučaju 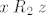 i i 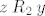 . .
Ako je 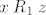 i i 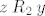 , onda je , onda je 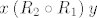 pa iz pa iz 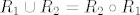 slijedi slijedi 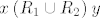 . .
Konačno, ako je 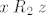 i i 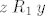 , zbog simetričnosti relacija , zbog simetričnosti relacija 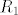 i i 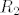 imamo imamo 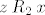 i i 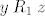 . Slijedi da je . Slijedi da je 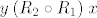 , tj. slično kao u prošlom slučaju, , tj. slično kao u prošlom slučaju, 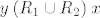 . Ali simetričnost . Ali simetričnost 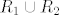 je evidentna jer su obje relacije je evidentna jer su obje relacije 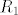 i i 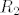 simetrične. simetrične.
Dakle, u svakom slučaju iz pretpostavke 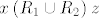 i i 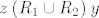 slijedi slijedi 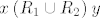 pa je to tranzitivna relacija. pa je to tranzitivna relacija.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
|








