| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 8:31 pet, 22. 1. 2010 Naslov: Postano: 8:31 pet, 22. 1. 2010 Naslov: |
    |
|
|
Tenx, moram priznat da ni ja nisam čuo za to, to me i muči... a što se zadatka tiče, tak sam ga prepisao sa kolokvija, može bit da sam nekaj fulao u prepisivanju, ali da sam fulao i x -> t i funkcija na dvije -> jedne varijable... hmmm...
Edit: funkcija je y(t)
Evo što sam našao za heunova metodu:
(...)druga metoda je poznata pod nazivom Heunova metoda. Dobije se za rješenja jednadžbi:
[img]http://www.zemris.fer.hr/predmeti/rg/diplomski/06Cizmek/images/image226.gif[/img], [img]http://www.zemris.fer.hr/predmeti/rg/diplomski/06Cizmek/images/image227.gif[/img], [img]http://www.zemris.fer.hr/predmeti/rg/diplomski/06Cizmek/images/image228.gif[/img], [img]http://www.zemris.fer.hr/predmeti/rg/diplomski/06Cizmek/images/image229.gif[/img] i glasi:
[img]http://www.zemris.fer.hr/predmeti/rg/diplomski/06Cizmek/images/image230.gif[/img]
Jel to to? Tu se nutra javlja f-ja dvije varijable... :?:
Tenx, moram priznat da ni ja nisam čuo za to, to me i muči... a što se zadatka tiče, tak sam ga prepisao sa kolokvija, može bit da sam nekaj fulao u prepisivanju, ali da sam fulao i x → t i funkcija na dvije → jedne varijable... hmmm...
Edit: funkcija je y(t)
Evo što sam našao za heunova metodu:
(...)druga metoda je poznata pod nazivom Heunova metoda. Dobije se za rješenja jednadžbi:
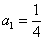 , , 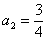 , , 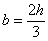 , , 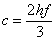 i glasi: i glasi:
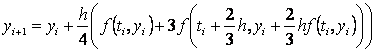
Jel to to? Tu se nutra javlja f-ja dvije varijable... 
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:15 ned, 24. 1. 2010 Naslov: Postano: 15:15 ned, 24. 1. 2010 Naslov: |
    |
|
|
Zbunjuje me slijedeće, ako imam funkciju [latex]e^{2x}[/latex], jel ona oblika za
[latex]f(x) = P(x)e^{\alpha x}(R(x)cos \beta x + Q(x)sin \beta x)[/latex]
gdje je [latex]\alpha=2[/latex]... E sad, s obzirom da funkcija nema [latex]sin[/latex] i [latex]cos[/latex] što si uzimam za [latex]\beta[/latex] i [latex]l=max(deg P, deg Q)[/latex]?
Jel uzimam: [latex]l=0 [/latex]
(od [latex]Q(x)[/latex] koji je ustvari [latex]1[/latex], pa [latex]\beta=0[/latex] (da ubijem član uz [latex]sin[/latex]) ili biram tak da da je [latex]R(x)=1[/latex], a [latex]Q(x) = nulpolinom[/latex], pa biram [latex]\beta[/latex] tak da ubijem član uz [latex]cos[/latex], ili mi je svejedno?
Zbunjuje me slijedeće, ako imam funkciju 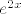 , jel ona oblika za , jel ona oblika za
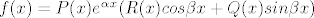
gdje je  ... E sad, s obzirom da funkcija nema ... E sad, s obzirom da funkcija nema 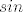 i i  što si uzimam za što si uzimam za 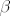 i i 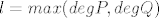 ? ?
Jel uzimam: 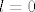
(od 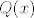 koji je ustvari koji je ustvari  , pa , pa 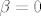 (da ubijem član uz (da ubijem član uz 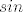 ) ili biram tak da da je ) ili biram tak da da je 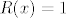 , a , a 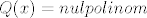 , pa biram , pa biram 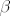 tak da ubijem član uz tak da ubijem član uz  , ili mi je svejedno? , ili mi je svejedno?
|
|
| [Vrh] |
|
tammy
Forumaš(ica)

Pridružen/a: 02. 07. 2007. (20:37:10)
Postovi: (197)16
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|













