| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
pmfovka
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (21:58:15)
Postovi: (60)16
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
:)
Forumaš(ica)
Pridružen/a: 25. 04. 2009. (16:17:14)
Postovi: (66)16
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 11:05 pon, 31. 10. 2011 Naslov: Postano: 11:05 pon, 31. 10. 2011 Naslov: |
    |
|
|
Prvi iz 2008 (B grupa).
Sve sto treba znati je sto je to afini prostor. U skladu s oznakama u zadatku, [latex](S,\mathbb{R}^2,f_S)[/latex] ce biti afini prostor, ako vrijedi:
[latex](\forall p\in S)(\forall x\in \mathbb{R}^2)(\exists ! q\in S)\quad f_S(p,q)=x[/latex]
i
[latex](\forall p,q,r\in S)\quad f_S(p,q)=f_S(p,r)+f_S(r,q)[/latex]
Sad odmah vidis da, da bi ovo prvo bilo zadovoljeno, moras fiksirati trecu koordinatu u [latex]S[/latex]. Inace bi za na primjer [latex](1,1,2)\in S[/latex] i [latex](0,0)\in \mathbb{R}^2[/latex] oba [latex]q_1=(1,1,2), q_2=(1,1,3)[/latex] zadovoljavali jednakost u prvom zahtjevu, pa trazeni [latex]q\in S[/latex] ne bi bio jedinstven.
Drugo je uvijek zadovoljeno, to se lako provijeri iz definicije [latex]f_S.[/latex] Dakle neki dobar [latex]S[/latex] bio bi [latex]S=\{(x,y,5)|x, y\in\mathbb{R}\}.[/latex]
Jeste dosli do kolokvija od prosle godine?
Prvi iz 2008 (B grupa).
Sve sto treba znati je sto je to afini prostor. U skladu s oznakama u zadatku, 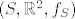 ce biti afini prostor, ako vrijedi: ce biti afini prostor, ako vrijedi:
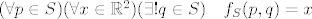
i
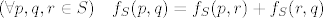
Sad odmah vidis da, da bi ovo prvo bilo zadovoljeno, moras fiksirati trecu koordinatu u  . Inace bi za na primjer . Inace bi za na primjer 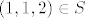 i i 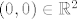 oba oba 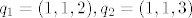 zadovoljavali jednakost u prvom zahtjevu, pa trazeni zadovoljavali jednakost u prvom zahtjevu, pa trazeni 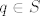 ne bi bio jedinstven. ne bi bio jedinstven.
Drugo je uvijek zadovoljeno, to se lako provijeri iz definicije 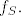 Dakle neki dobar Dakle neki dobar  bio bi bio bi 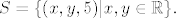
Jeste dosli do kolokvija od prosle godine?
_________________
Mario Berljafa
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 2:08 uto, 1. 11. 2011 Naslov: Postano: 2:08 uto, 1. 11. 2011 Naslov: |
    |
|
|
jedno pitanje. nije mi jasno ovdje [url]http://web.math.hr/nastava/eukl/ZAD_12.pdf[/url], u 1.zadatku pod (b) imamo A=R^3, V=R^2, i funkciju v ovako kako je definirana.
ja dobijem da to nije afin prostor, jer prvo svojstvo nije zadovoljeno, s obzirom da postoji beskonacno mnogo elemenata y iz A koji zadovoljavaju v(x,y)=a, bas zato sto se mozemo "setati" po trecoj koordinati. no u rjesenju pise da je pod (b) u pitanju afin prostor. pa me zanima jesam li nesto fulao ili je greska u rjesenju? fala :)
jedno pitanje. nije mi jasno ovdje http://web.math.hr/nastava/eukl/ZAD_12.pdf, u 1.zadatku pod (b) imamo A=R^3, V=R^2, i funkciju v ovako kako je definirana.
ja dobijem da to nije afin prostor, jer prvo svojstvo nije zadovoljeno, s obzirom da postoji beskonacno mnogo elemenata y iz A koji zadovoljavaju v(x,y)=a, bas zato sto se mozemo "setati" po trecoj koordinati. no u rjesenju pise da je pod (b) u pitanju afin prostor. pa me zanima jesam li nesto fulao ili je greska u rjesenju? fala 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Ramone
Gost
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 12:41 pon, 7. 11. 2011 Naslov: Postano: 12:41 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote="Ramone"]Kako bi isao ovaj 1., prošla godina?[/quote]
ja bih rekao da ne postoji lambda iz R takav da je dana trojka afin prostor. padamo vec na svojstvu A1:
za svaki x iz R, i za svaki (z1,z2) iz R^2, mora postojati jedinstveni y iz R takav da je v(x,y)=(z1,z2)
znamo da je v(x,y)=(y-x,lambda), pa kad izjednacimo prve koordinate dobijemo
z1 = y - x => y = z1+x, i to je u redu, medjutim kad izjednacimo druge koordinate, dobijemo da mora vrijediti
z2=lambda.
a ne postoji realan broj lambda tako da za svaki z2 realan broj vrijedi z2=lambda.
| Ramone (napisa): | | Kako bi isao ovaj 1., prošla godina? |
ja bih rekao da ne postoji lambda iz R takav da je dana trojka afin prostor. padamo vec na svojstvu A1:
za svaki x iz R, i za svaki (z1,z2) iz R^2, mora postojati jedinstveni y iz R takav da je v(x,y)=(z1,z2)
znamo da je v(x,y)=(y-x,lambda), pa kad izjednacimo prve koordinate dobijemo
z1 = y - x ⇒ y = z1+x, i to je u redu, medjutim kad izjednacimo druge koordinate, dobijemo da mora vrijediti
z2=lambda.
a ne postoji realan broj lambda tako da za svaki z2 realan broj vrijedi z2=lambda.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 13:57 pon, 7. 11. 2011 Naslov: Postano: 13:57 pon, 7. 11. 2011 Naslov: |
    |
|
|
Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y -> y=x-a i ni jedan drugi. Druga koordinata što god da bila ne utječe na to.
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0.
Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y -> y=x-a i ni jedan drugi. Druga koordinata što god da bila ne utječe na to.
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0.
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 14:20 pon, 7. 11. 2011 Naslov: Postano: 14:20 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote=".anchy."]Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y -> y=x-a i ni jedan drugi. [b]Druga koordinata što god da bila ne utječe na to.[/b]
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0.[/quote]
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi?
| .anchy. (napisa): | Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y → y=x-a i ni jedan drugi. Druga koordinata što god da bila ne utječe na to.
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0. |
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
Added after 11 minutes:
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi?
|
|
| [Vrh] |
|
ddujmic
Forumaš(ica)

Pridružen/a: 17. 02. 2009. (14:01:31)
Postovi: (75)16
|
 Postano: 14:37 pon, 7. 11. 2011 Naslov: Postano: 14:37 pon, 7. 11. 2011 Naslov: |
    |
|
|
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Kodomena je RxR
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="stuey"][quote=".anchy."]Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y -> y=x-a i ni jedan drugi. [b]Druga koordinata što god da bila ne utječe na to.[/b]
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0.[/quote]
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi?[/quote]
Ako je konacnodim, onda su afini i pripadni vekt. istih dimenzija. Kao sto su neka ravnina i pripadni smjer
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Kodomena je RxR
Added after 6 minutes:
| stuey (napisa): | | .anchy. (napisa): | Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y → y=x-a i ni jedan drugi. Druga koordinata što god da bila ne utječe na to.
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0. |
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
Added after 11 minutes:
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi? |
Ako je konacnodim, onda su afini i pripadni vekt. istih dimenzija. Kao sto su neka ravnina i pripadni smjer
_________________
Nothing lasts forever
Even cold November rain
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 19:13 pon, 7. 11. 2011 Naslov: Postano: 19:13 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote="stuey"][quote=".anchy."]Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y -> y=x-a i ni jedan drugi. [b]Druga koordinata što god da bila ne utječe na to.[/b]
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0.[/quote]
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi?[/quote]
Mislila sam da ne utječe na način:
npr lambda=1:
A1 za svaki x iz A, za svaki z iz V=R2 postoji jedinstven y td. v(x,y)=z.
stavimo z=(a,1), uzmimo x i z proizvoljne. Trebamo dokazati da postoji jedinstven y t.d. v(x,y)=z=(a,1).
a=x-y <=> y=x-a
slijedi y je jednistven
za lambda=0, dobimo isti y, na taj način ne ovisi.
a afini prostor i vektorski ne moraju biti iste dimenzije,već u ovom zadatku nisu:
Afini prostor je R, a vektorski prostor RxR,još jedan primjer v(x,y)=(y-x,y-x).
Nisam 100 % sigurna,najbolje bi bilo kada bi netko od demosa,asistenata to razjasnio..
[size=9][color=#999999]Added after 35 minutes:[/color][/size]
Sada mi je asistent Iljazović odgovorio na mail(u roku od 20-tak min :shock: ), i imali ste pravo,takav lambda ne postoji.
Gdje ja griješim u onom što sam napisala?
| stuey (napisa): | | .anchy. (napisa): | Ne bih se složila.. mislim da je lambda=0.
Ovaj prvi uvjet je ustvari zadovoljen za svaki lambda,ali srugi uvjet(zbrajanje vektora nije).
Jer, označimo vektor iz kodomene sa z. Tada za svaki z,i svaki x mora postojati jedinstven y t.d. v(x,y)=z.
Prva koordinata od z (nazovimo ju a) nam daje tu jedinstvenost:
a=x-y → y=x-a i ni jedan drugi. Druga koordinata što god da bila ne utječe na to.
Ali v(x,y)=v(x,z)+v(z,y) je zadovoljena samo za lambda=0. |
ovo boldano... kako misliš da druga koordinata ne utječe na to? tekst zadatka kaže da je v(x,y) = (y-x, lambda), dakle druga koordinata mora biti lambda. recimo da je z=(a,b), to znači da za svaki realan broj b mora vrijediti b=lambda.
kako god da fiksiraš lambda (ti si ga fiksirala kao lambda=0), to je neistinita tvrdnja.
Added after 11 minutes:
i inače, mislim da afin prostor i pripadni vektorski prostor moraju biti istih dimenzija. odnosno, da uopće ne postoji funkcija v takva da je (R, RxR, v) afin prostor.
ili općenito, ako imamo da je (A^m, V^n, v) afin prostor, da tad mora vrijediti m=n. može li ovo netko potvrditi? |
Mislila sam da ne utječe na način:
npr lambda=1:
A1 za svaki x iz A, za svaki z iz V=R2 postoji jedinstven y td. v(x,y)=z.
stavimo z=(a,1), uzmimo x i z proizvoljne. Trebamo dokazati da postoji jedinstven y t.d. v(x,y)=z=(a,1).
a=x-y ⇔ y=x-a
slijedi y je jednistven
za lambda=0, dobimo isti y, na taj način ne ovisi.
a afini prostor i vektorski ne moraju biti iste dimenzije,već u ovom zadatku nisu:
Afini prostor je R, a vektorski prostor RxR,još jedan primjer v(x,y)=(y-x,y-x).
Nisam 100 % sigurna,najbolje bi bilo kada bi netko od demosa,asistenata to razjasnio..
Added after 35 minutes:
Sada mi je asistent Iljazović odgovorio na mail(u roku od 20-tak min  ), i imali ste pravo,takav lambda ne postoji. ), i imali ste pravo,takav lambda ne postoji.
Gdje ja griješim u onom što sam napisala?
|
|
| [Vrh] |
|
stuey
Forumaš(ica)


Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol: 
Lokacija: Rijeka, Zg
|
 Postano: 19:24 pon, 7. 11. 2011 Naslov: Postano: 19:24 pon, 7. 11. 2011 Naslov: |
    |
|
|
@ddujmic: hvala ;)
@anchy:
[quote=".anchy."]
Mislila sam da ne utječe na način:
npr lambda=1:
A1 za svaki x iz A, za svaki z iz V=R2 postoji jedinstven y td. v(x,y)=z.
[b]stavimo z=(a,1)[/b], uzmimo x i z proizvoljne. Trebamo dokazati da postoji jedinstven y t.d. v(x,y)=z=(a,1).
a=x-y <=> y=x-a
slijedi y je jednistven
za lambda=0, dobimo isti y, na taj način ne ovisi.[/quote]
pogledaj ovo boldano.. kazes "stavimo z=(a,1)". ako smo prethodno odabrali lambda=1, tada ce zaista za z=(a,1) postojati jedinstveni y iz A, takav da je v(x,y)=z. medjutim, to mora vrijediti za svaki z, a ovdje vrijedi samo za z-ove kojima je druga koordinata 1. za sve ostale z-ove to uopce ne vrijedi.
ili opcenito, koji god lambda da uzmes, ta tvrdnja ce vrijediti samo za one z-ove koji imaju za drugu koordinatu lambda, a za sve ostale z-ove nece vrijediti. sto nam ne pase jer, [i]jednom kad odaberemo lambdu[/i], tvrdnja mora vrijediti za sve z-ove iz R^2.
dakle, nemamo problema s prvom koordinatom iz koje lako izvucemo taj jedinstveni y, ali to nam ovdje ne igra ulogu jer padamo na drugoj koordinati.
[quote=".anchy."]
a afini prostor i vektorski ne moraju biti iste dimenzije,već u ovom zadatku nisu:
Afini prostor je R, a vektorski prostor RxR,još jedan primjer v(x,y)=(y-x,y-x).
Nisam 100 % sigurna,najbolje bi bilo kada bi netko od demosa,asistenata to razjasnio..[/quote]
taj primjer koji si dala nije afin prostor. opet padas na A1:
za svaki x iz R, i za svaki (z1,z2) iz R^2, mora postojati jedinstveni y iz R, takav da je v(x,y)=(z1,z2).
dala si primjer v(x,y)=(y-x,y-x), pa kad izjednacimo koordinate dobijemo:
y-x=z1
y-x=z2
iz prve jednakosti slijedi y=x+z1, a kad to uvrstimo u drugu, dobijemo z1=z2.
dakle, svojstvo A1 bi vrijedilo samo za one (z1,z2) iz R^2 za koje vrijedi z1=z2, odnosno to je pravac y=x.
a taj pravac je dimenzije 1, bas kao i afin prostor :)
@ddujmic: hvala 
@anchy:
| .anchy. (napisa): |
Mislila sam da ne utječe na način:
npr lambda=1:
A1 za svaki x iz A, za svaki z iz V=R2 postoji jedinstven y td. v(x,y)=z.
stavimo z=(a,1), uzmimo x i z proizvoljne. Trebamo dokazati da postoji jedinstven y t.d. v(x,y)=z=(a,1).
a=x-y ⇔ y=x-a
slijedi y je jednistven
za lambda=0, dobimo isti y, na taj način ne ovisi. |
pogledaj ovo boldano.. kazes "stavimo z=(a,1)". ako smo prethodno odabrali lambda=1, tada ce zaista za z=(a,1) postojati jedinstveni y iz A, takav da je v(x,y)=z. medjutim, to mora vrijediti za svaki z, a ovdje vrijedi samo za z-ove kojima je druga koordinata 1. za sve ostale z-ove to uopce ne vrijedi.
ili opcenito, koji god lambda da uzmes, ta tvrdnja ce vrijediti samo za one z-ove koji imaju za drugu koordinatu lambda, a za sve ostale z-ove nece vrijediti. sto nam ne pase jer, jednom kad odaberemo lambdu, tvrdnja mora vrijediti za sve z-ove iz R^2.
dakle, nemamo problema s prvom koordinatom iz koje lako izvucemo taj jedinstveni y, ali to nam ovdje ne igra ulogu jer padamo na drugoj koordinati.
| .anchy. (napisa): |
a afini prostor i vektorski ne moraju biti iste dimenzije,već u ovom zadatku nisu:
Afini prostor je R, a vektorski prostor RxR,još jedan primjer v(x,y)=(y-x,y-x).
Nisam 100 % sigurna,najbolje bi bilo kada bi netko od demosa,asistenata to razjasnio.. |
taj primjer koji si dala nije afin prostor. opet padas na A1:
za svaki x iz R, i za svaki (z1,z2) iz R^2, mora postojati jedinstveni y iz R, takav da je v(x,y)=(z1,z2).
dala si primjer v(x,y)=(y-x,y-x), pa kad izjednacimo koordinate dobijemo:
y-x=z1
y-x=z2
iz prve jednakosti slijedi y=x+z1, a kad to uvrstimo u drugu, dobijemo z1=z2.
dakle, svojstvo A1 bi vrijedilo samo za one (z1,z2) iz R^2 za koje vrijedi z1=z2, odnosno to je pravac y=x.
a taj pravac je dimenzije 1, bas kao i afin prostor 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
|








