| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 21:50 pon, 3. 1. 2011 Naslov: Postano: 21:50 pon, 3. 1. 2011 Naslov: |
    |
|
|
http://web.math.hr/nastava/analiza/files/ma1-zadaca5.pdf
moze pomoc oko 7., i 12? ako je netko voljan i 17 =)) hvalaaa!
i jedno pitanje, zadatak 13. pod a)
ovdje sam dodala jedinicu i oduzela je,i u brojniku i u nazivniku...sada,dobijem izraze koje bi mogla dijeliti sa x^2 tako da iskoristim poznate limese za kosinus i kosinus hiperbolni,ili mogu dijeliti sa x,pa dobijem poznate limese oblike (a^x-1)/x=lna....Wolfram kaze da treba dijeliti s x,a zasto???
http://www.wolframalpha.com/input/?i=lim%28x-%3E0%29+%28+2^x-cos%28x%29%29+%2F+%283^x-cosh%28x%29%29+
http://web.math.hr/nastava/analiza/files/ma1-zadaca5.pdf
moze pomoc oko 7., i 12? ako je netko voljan i 17 =)) hvalaaa!
i jedno pitanje, zadatak 13. pod a)
ovdje sam dodala jedinicu i oduzela je,i u brojniku i u nazivniku...sada,dobijem izraze koje bi mogla dijeliti sa x^2 tako da iskoristim poznate limese za kosinus i kosinus hiperbolni,ili mogu dijeliti sa x,pa dobijem poznate limese oblike (a^x-1)/x=lna....Wolfram kaze da treba dijeliti s x,a zasto???
http://www.wolframalpha.com/input/?i=lim%28x-%3E0%29+%28+2^x-cos%28x%29%29+%2F+%283^x-cosh%28x%29%29+
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 22:04 pon, 3. 1. 2011 Naslov: Postano: 22:04 pon, 3. 1. 2011 Naslov: |
    |
|
|
7. Po definiciji (neprekidnosti funkcije u određenoj točki), funkcija iz zadatka je neprekidna ako postoji limes u toj točki i ako je [latex]\displaystyle\lim_{x\to c}f(x) = f(c)[/latex]. Dakle, odredš limes zdesna i limes slijeva funkcije f u točki 0 i provjeriš jesu li jednaki. U slučaju da jesu, postavi jednadžbu [latex]\displaystyle\lim_{x\to 0}f(x) = f(0)[/latex], a onda zapravo uvrštavanjem dobivaš rješenje.
12. Funkcija nije neprekidna u točki [latex]x = 1[/latex], pa tražimo limes zdesna i limes slijeva u točki 1. Opet: ako su limesi jednaki (i ako su u skupu realnih brojeva, odnosno da limes nije jednak nijednoj od beskonačnosti), onda posebno definiraš f(1) kao [latex]f(1) = \displaystyle\lim_{x\to 1}f(x)[/latex]. U suprotnom slučaju, ako su različiti ili ako je bilo koji limes jednak nekoj od beskonačnosti, funkcija se ne može proširiti do neprekidne funkcije na skupu realnih brojeva.
17. Sasvim analogno kao i u 12. zadatku.
13. a) Mislim da ti izraz [latex]\frac{a^x - 1}{x^2}[/latex] u okviru limesa ne pomaže previše (barem kada x teži u nulu). S druge strane, ako podijeliš samo s x, a onda drugi limes prikažeš kao [latex]x * (izraz-koji-ti-odgovara)[/latex], samo trebaš uvrstiti vrijednosti pojedinačnih limesa i zadatak je gotov.
7. Po definiciji (neprekidnosti funkcije u određenoj točki), funkcija iz zadatka je neprekidna ako postoji limes u toj točki i ako je 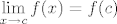 . Dakle, odredš limes zdesna i limes slijeva funkcije f u točki 0 i provjeriš jesu li jednaki. U slučaju da jesu, postavi jednadžbu . Dakle, odredš limes zdesna i limes slijeva funkcije f u točki 0 i provjeriš jesu li jednaki. U slučaju da jesu, postavi jednadžbu 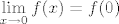 , a onda zapravo uvrštavanjem dobivaš rješenje. , a onda zapravo uvrštavanjem dobivaš rješenje.
12. Funkcija nije neprekidna u točki  , pa tražimo limes zdesna i limes slijeva u točki 1. Opet: ako su limesi jednaki (i ako su u skupu realnih brojeva, odnosno da limes nije jednak nijednoj od beskonačnosti), onda posebno definiraš f(1) kao , pa tražimo limes zdesna i limes slijeva u točki 1. Opet: ako su limesi jednaki (i ako su u skupu realnih brojeva, odnosno da limes nije jednak nijednoj od beskonačnosti), onda posebno definiraš f(1) kao 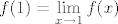 . U suprotnom slučaju, ako su različiti ili ako je bilo koji limes jednak nekoj od beskonačnosti, funkcija se ne može proširiti do neprekidne funkcije na skupu realnih brojeva. . U suprotnom slučaju, ako su različiti ili ako je bilo koji limes jednak nekoj od beskonačnosti, funkcija se ne može proširiti do neprekidne funkcije na skupu realnih brojeva.
17. Sasvim analogno kao i u 12. zadatku.
13. a) Mislim da ti izraz 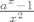 u okviru limesa ne pomaže previše (barem kada x teži u nulu). S druge strane, ako podijeliš samo s x, a onda drugi limes prikažeš kao u okviru limesa ne pomaže previše (barem kada x teži u nulu). S druge strane, ako podijeliš samo s x, a onda drugi limes prikažeš kao 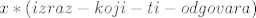 , samo trebaš uvrstiti vrijednosti pojedinačnih limesa i zadatak je gotov. , samo trebaš uvrstiti vrijednosti pojedinačnih limesa i zadatak je gotov.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:54 sri, 5. 1. 2011 Naslov: Postano: 13:54 sri, 5. 1. 2011 Naslov: |
    |
|
|
Pretpostavljam da si to transformirao na način [latex]\displaystyle t:=x+\frac{\pi}{2}[/latex]. Okej, to je dobro. :P (Možda malo nepotrebno, ali sasvim dobro. :D)
Dakle, sad tebe zapravo zanima (kad si iskoristio ovu formulu iz tablice) limes od [latex]\displaystyle(\tan(\frac{\pi}{4}\cos(t))-1)\cot(\pi\cos(t))[/latex] za [latex]t \to 0[/latex]. E, sad, što bih ja tu napravio...
Aha, idemo ovako probati. Ajde uzmimo [latex]u:=\cos(t)-1[/latex], da se riješimo kosinusa. Primijetimo da sad, ako [latex]t\to 0[/latex], [latex]u\to 0[/latex]. Naravno, kako limes gore ovisi samo o [latex]\cos(t)[/latex], a nigdje "direktno" o [latex]t[/latex], nemamo nikakvih problema s ovom supstitucijom. Ako te baš interesira formaliziranje, to si možda možeš raspisati. :)
Dakle, tražimo limes of [latex]\displaystyle(\tan(\frac{\pi}{4}u+\frac{\pi}{4})-1)\cot(\pi u+\pi)[/latex] za [latex]u\to 0[/latex]. No dobro, kotangens ima period [latex]\pi[/latex], tako da je [latex]\cot(\pi u+\pi)=\cot(\pi u)[/latex], a u tangensu možemo iskoristiti adicijske formule i dobiti [latex]\displaystyle\tan(\frac{\pi}{4}u+\frac{\pi}{4})=\frac{\tan(\frac{\pi}{4}u)+1}{1-\tan(\frac{\pi}{4}u)}[/latex].
Sad smo već na konju. :) Naime, dobivamo (sređivanjem s ovom minus jedinicom kraj tangensa na početku) da je naš izraz zapravo [latex]\displaystyle\frac{2\tan(\frac{\pi}{4}u)\cot(\pi u)}{1-\tan(\frac{\pi}{4}u)}[/latex].
E, a ovo tu nam nije neki veliki problem. Znamo limes od [latex]\displaystyle\frac{\tan(\frac{\pi}{4}u)}{u}=\frac{\pi}{4}\frac{\tan(\frac{\pi}{4}u)}{\frac{\pi}{4}u}[/latex] - to je [latex]\displaystyle\frac{\pi}{4}[/latex].
Također, znamo i limes od [latex]\displaystyle u\cot(\pi u)=\frac{1}{\pi}\cdot \frac{\pi u}{\tan(\pi u)}[/latex] - to je [latex]\displaystyle\frac{1}{\pi}[/latex] osobno. Budući da nam nazivnik ide u [latex]1-0=1[/latex], cijeli gornji limes bi valjda trebao biti [latex]\displaystyle\frac{1}{2}[/latex], što bi reklo da je rješenje zadatka [latex]\sqrt{e}[/latex].
Uh. :D
Pretpostavljam da si to transformirao na način 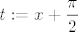 . Okej, to je dobro. . Okej, to je dobro.  (Možda malo nepotrebno, ali sasvim dobro. (Možda malo nepotrebno, ali sasvim dobro.  ) )
Dakle, sad tebe zapravo zanima (kad si iskoristio ovu formulu iz tablice) limes od 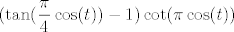 za za 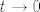 . E, sad, što bih ja tu napravio... . E, sad, što bih ja tu napravio...
Aha, idemo ovako probati. Ajde uzmimo 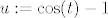 , da se riješimo kosinusa. Primijetimo da sad, ako , da se riješimo kosinusa. Primijetimo da sad, ako 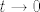 , , 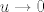 . Naravno, kako limes gore ovisi samo o . Naravno, kako limes gore ovisi samo o 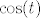 , a nigdje "direktno" o , a nigdje "direktno" o  , nemamo nikakvih problema s ovom supstitucijom. Ako te baš interesira formaliziranje, to si možda možeš raspisati. , nemamo nikakvih problema s ovom supstitucijom. Ako te baš interesira formaliziranje, to si možda možeš raspisati. 
Dakle, tražimo limes of 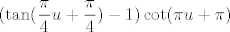 za za 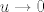 . No dobro, kotangens ima period . No dobro, kotangens ima period  , tako da je , tako da je 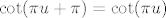 , a u tangensu možemo iskoristiti adicijske formule i dobiti , a u tangensu možemo iskoristiti adicijske formule i dobiti 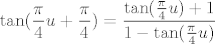 . .
Sad smo već na konju.  Naime, dobivamo (sređivanjem s ovom minus jedinicom kraj tangensa na početku) da je naš izraz zapravo Naime, dobivamo (sređivanjem s ovom minus jedinicom kraj tangensa na početku) da je naš izraz zapravo 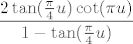 . .
E, a ovo tu nam nije neki veliki problem. Znamo limes od 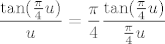 - to je - to je  . .
Također, znamo i limes od 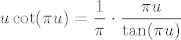 - to je - to je 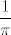 osobno. Budući da nam nazivnik ide u osobno. Budući da nam nazivnik ide u 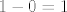 , cijeli gornji limes bi valjda trebao biti , cijeli gornji limes bi valjda trebao biti  , što bi reklo da je rješenje zadatka , što bi reklo da je rješenje zadatka 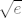 . .
Uh. 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
avicii
Forumaš(ica)

Pridružen/a: 07. 01. 2010. (21:07:05)
Postovi: (3)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:35 sri, 5. 1. 2011 Naslov: Postano: 19:35 sri, 5. 1. 2011 Naslov: |
    |
|
|
A u vezi 11. b) i c) - pa dobro, ideja za b) ti u načelu nije loša: u nazivniku bih koristio, što si i rekao, da je [latex]\displaystyle a-b=\frac{a^2-b^2}{a+b}[/latex], a u brojniku da je [latex]\displaystyle a-b=\frac{a^3-b^3}{a^2+ab+b^2}[/latex]. Kad to staviš unutra (uz, naravno, prikladni odabir [latex]a[/latex] i [latex]b[/latex] koji je dosta očit :D), jamčim da će se pokratiti sve sumnjivo. :)
Rješenje od c) ćeš naći pri kraju [url=http://degiorgi.math.hr/forum/viewtopic.php?p=129538#129538]ovog gigantskog posta[/url] (bar se nadam da je to isti zadatak :P) - ideja dokazivanja je slična kao u b), a poanta je da to uopće nije neodređen oblik (evo, ako te ne zanima gotovo rješenje u ovom trenutku, na čemu aplaudiram, mislim da je to i sasvim legalan hint :)).
A u vezi 11. b) i c) - pa dobro, ideja za b) ti u načelu nije loša: u nazivniku bih koristio, što si i rekao, da je 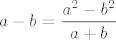 , a u brojniku da je , a u brojniku da je 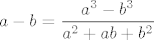 . Kad to staviš unutra (uz, naravno, prikladni odabir . Kad to staviš unutra (uz, naravno, prikladni odabir  i i 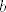 koji je dosta očit koji je dosta očit  ), jamčim da će se pokratiti sve sumnjivo. ), jamčim da će se pokratiti sve sumnjivo. 
Rješenje od c) ćeš naći pri kraju ovog gigantskog posta (bar se nadam da je to isti zadatak  ) - ideja dokazivanja je slična kao u b), a poanta je da to uopće nije neodređen oblik (evo, ako te ne zanima gotovo rješenje u ovom trenutku, na čemu aplaudiram, mislim da je to i sasvim legalan hint ) - ideja dokazivanja je slična kao u b), a poanta je da to uopće nije neodređen oblik (evo, ako te ne zanima gotovo rješenje u ovom trenutku, na čemu aplaudiram, mislim da je to i sasvim legalan hint  ). ).
|
|
| [Vrh] |
|
|












