| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
 Postano: 18:36 pet, 21. 10. 2011 Naslov: Postano: 18:36 pet, 21. 10. 2011 Naslov: |
    |
|
|
Pa, pošto ne znamo baš svojstva beskonačno dimenzionalnih, najlakše je pretpostaviti suprotno - on je konačno dimenzionalan. A to znači da ima bazu. Recimo da mu je dimenzija n. Definirajmo niz nizova (:D) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. [latex]a_1[/latex] će biti niz 1, 0, 0, 0..., [latex]a_2[/latex] će biti niz 0, 1, 0, 0, 0... itd.
Lako se pokaže da su svi [latex]a_i[/latex] linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, [latex]a_1[/latex] do [latex]a_n[/latex]. Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz [latex]a_{n+1}[/latex], njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan.
Pa, pošto ne znamo baš svojstva beskonačno dimenzionalnih, najlakše je pretpostaviti suprotno - on je konačno dimenzionalan. A to znači da ima bazu. Recimo da mu je dimenzija n. Definirajmo niz nizova ( ) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. ) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. 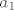 će biti niz 1, 0, 0, 0..., će biti niz 1, 0, 0, 0..., 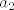 će biti niz 0, 1, 0, 0, 0... itd. će biti niz 0, 1, 0, 0, 0... itd.
Lako se pokaže da su svi 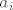 linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, 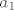 do do 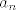 . Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz . Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz 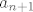 , njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan. , njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan.
_________________
Ceterum censeo Carthaginem esse delendam.
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 19:07 pet, 21. 10. 2011 Naslov: Postano: 19:07 pet, 21. 10. 2011 Naslov: |
    |
|
|
[quote="Borgcube"]Pa, pošto ne znamo baš svojstva beskonačno dimenzionalnih, najlakše je pretpostaviti suprotno - on je konačno dimenzionalan. A to znači da ima bazu. Recimo da mu je dimenzija n. Definirajmo niz nizova (:D) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. [latex]a_1[/latex] će biti niz 1, 0, 0, 0..., [latex]a_2[/latex] će biti niz 0, 1, 0, 0, 0... itd.
Lako se pokaže da su svi [latex]a_i[/latex] linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, [latex]a_1[/latex] do [latex]a_n[/latex]. Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz [latex]a_{n+1}[/latex], njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan.[/quote]
Puno hvala, shvatio sam!
| Borgcube (napisa): | Pa, pošto ne znamo baš svojstva beskonačno dimenzionalnih, najlakše je pretpostaviti suprotno - on je konačno dimenzionalan. A to znači da ima bazu. Recimo da mu je dimenzija n. Definirajmo niz nizova ( ) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. ) td. da i-ti niz ima sve članove nula, osim i-tog koji je jedan. Dakle, npr. 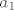 će biti niz 1, 0, 0, 0..., će biti niz 1, 0, 0, 0..., 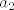 će biti niz 0, 1, 0, 0, 0... itd. će biti niz 0, 1, 0, 0, 0... itd.
Lako se pokaže da su svi 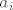 linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, linearno nezavisni - primjerice indukcijom. Sad uzmemo n takvih nizova, 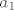 do do 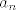 . Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz . Pošto su linearno nezavisni, i n ih je, oni čine bazu. No, ako uzmemo niz 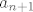 , njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan. , njega ne možemo prikazati preko prethodnih, što znači da oni nisu baza, a kako jesu linearno nezavisni, znači da nisu sistem izvodnica. No, to je kontradikcija s pretpostavkom da je taj prostor konačno dimenzionalan. |
Puno hvala, shvatio sam!
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
 Postano: 11:05 sub, 22. 10. 2011 Naslov: Postano: 11:05 sub, 22. 10. 2011 Naslov: |
    |
|
|
sto se tice 4. zad., nama je asistent rekao da trebamo pokazat samo da je lin. ljuska od A podskup od lin.ljuske od B i obratno...
pa sam ja to ovako dokazala....
Neka je lin.lj. od A podskup od lin.lj. od B te neka je x=suma svih alfa(i)*a(i), i=1,...,r. treba dokazati da je xE lin.lj. A ujedno i E lin.lj. B.
ako je xE lin.lj.B, tada se on moze prikazati kao lin.komb. svih bj, tj. x=suma svih beta(j)*b(j), j=1,...,s. kako je xE lin.lj. A, iz pretpostavke da je lin.lj. A podskup od lin.lj. B slijedi da je xE lin.lj. B sto povlaci da je suma svih alfa(i)*a(i) E lin.lj. B, tj. a(i) E lin.lj. B za svaki i=1,...,r.
analogno i za lin.lj. B podskup lin. ljuske A.........
jel to dobro???
e,a kak ovaj 5.? mislim, ja bi to isla dokazat na sljedeci nacin: da uzmem konacan skup B podskup od Rn koji ima konacno elemenata k....i sad je i taj skup lin.nez. jer je i Rn linearno nezavisan...i sad...kako uopce izgleda opci clan niza realnih brojeva??
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
ahaa... sad sam vidjela ovo objasnjenje za 5. zad...jasno mi je sve, samo zasto smo smjeli tako uzet da stavimo a1=(1,0,...), itd... onda je to jednostavno jer je to isto kao sto nam je prof. objasnio za e-ove....
sto se tice 4. zad., nama je asistent rekao da trebamo pokazat samo da je lin. ljuska od A podskup od lin.ljuske od B i obratno...
pa sam ja to ovako dokazala....
Neka je lin.lj. od A podskup od lin.lj. od B te neka je x=suma svih alfa(i)*a(i), i=1,...,r. treba dokazati da je xE lin.lj. A ujedno i E lin.lj. B.
ako je xE lin.lj.B, tada se on moze prikazati kao lin.komb. svih bj, tj. x=suma svih beta(j)*b(j), j=1,...,s. kako je xE lin.lj. A, iz pretpostavke da je lin.lj. A podskup od lin.lj. B slijedi da je xE lin.lj. B sto povlaci da je suma svih alfa(i)*a(i) E lin.lj. B, tj. a(i) E lin.lj. B za svaki i=1,...,r.
analogno i za lin.lj. B podskup lin. ljuske A.........
jel to dobro???
e,a kak ovaj 5.? mislim, ja bi to isla dokazat na sljedeci nacin: da uzmem konacan skup B podskup od Rn koji ima konacno elemenata k....i sad je i taj skup lin.nez. jer je i Rn linearno nezavisan...i sad...kako uopce izgleda opci clan niza realnih brojeva??
Added after 5 minutes:
ahaa... sad sam vidjela ovo objasnjenje za 5. zad...jasno mi je sve, samo zasto smo smjeli tako uzet da stavimo a1=(1,0,...), itd... onda je to jednostavno jer je to isto kao sto nam je prof. objasnio za e-ove....
|
|
| [Vrh] |
|
lav
Forumaš(ica)

Pridružen/a: 18. 10. 2011. (12:50:51)
Postovi: (5)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
 Postano: 13:02 ned, 23. 10. 2011 Naslov: Postano: 13:02 ned, 23. 10. 2011 Naslov: |
    |
|
|
kako dokazati da je nešto sustav izvodnica? jel dovoljno napisati a1(1,1,1)+a2(2,1,3)+a3(3,1,7)+a4(6,2,12)=(v1,v2,v3) ?
kako dokazati da je nešto sustav izvodnica? jel dovoljno napisati a1(1,1,1)+a2(2,1,3)+a3(3,1,7)+a4(6,2,12)=(v1,v2,v3) ?
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 13:47 ned, 23. 10. 2011 Naslov: Postano: 13:47 ned, 23. 10. 2011 Naslov: |
    |
|
|
Ili ima beskonacno rjesenja ili uopce nema rjesenja.
[quote="gflegar"]Dovoljno je pokazati da se opci clan v. p. moze prikazati kao lin. komb. skupa za koji hoces pokazati da je sustav izvodnica. U tvojem slucaju, treba rijesiti ovaj sustav jednadzbi po [tex] a_1, a_2, a_3[/tex]. Taj je skup tada sustav izvodnica ako sustav jednadzbi ima rjesenje.[/quote]
Ako ima beskonacno rjesenja, tada je jasno da i ima rjesenje, pa je i sustav izvodnica. :D
[size=9][color=#999999]Added after 15 minutes:[/color][/size]
[quote="jema"]5. zadatak??? :D[/quote]
Sto ti tocno nije jasno u rjesenju kojeg je napisao/la Borgcube?
Ili ima beskonacno rjesenja ili uopce nema rjesenja.
| gflegar (napisa): | | Dovoljno je pokazati da se opci clan v. p. moze prikazati kao lin. komb. skupa za koji hoces pokazati da je sustav izvodnica. U tvojem slucaju, treba rijesiti ovaj sustav jednadzbi po [tex] a_1, a_2, a_3[/tex]. Taj je skup tada sustav izvodnica ako sustav jednadzbi ima rjesenje. |
Ako ima beskonacno rjesenja, tada je jasno da i ima rjesenje, pa je i sustav izvodnica. 
Added after 15 minutes:
| jema (napisa): | 5. zadatak???  |
Sto ti tocno nije jasno u rjesenju kojeg je napisao/la Borgcube?
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
 Postano: 19:51 ned, 23. 10. 2011 Naslov: Postano: 19:51 ned, 23. 10. 2011 Naslov: |
    |
|
|
a mislim, jasno mi je sve sto je on/a napisalo/la, samo mi cudno to kak se moze uzeti da mi je a1 niz (1,0,0,...), itd... XD al dobro :) a jel dobar moj dokaz za 4.zad?? XD :)
a mislim, jasno mi je sve sto je on/a napisalo/la, samo mi cudno to kak se moze uzeti da mi je a1 niz (1,0,0,...), itd... XD al dobro  a jel dobar moj dokaz za 4.zad?? XD a jel dobar moj dokaz za 4.zad?? XD 
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 20:33 ned, 23. 10. 2011 Naslov: Postano: 20:33 ned, 23. 10. 2011 Naslov: |
    |
|
|
A zasto nebi smjeli uzeti taj skup? Nismo morali bas njega uzeti, ali je on nekako najjednostavniji za dobiti kontradikciju. Jer je cijeli smisao dokaza ovaj: uzmes neki skup, dokazes da je on baza, a onda dokazes da on istovremeno nije baza, pa dobis kontradikciju. :D
[size=9][color=#999999]Added after 14 minutes:[/color][/size]
[quote="jema"]
Neka je lin.lj. od A podskup od lin.lj. od B te neka je x=suma svih alfa(i)*a(i), i=1,...,r. treba dokazati da je xE lin.lj. A ujedno i E lin.lj. B.
[/quote]
Ako sam ja dobro ovo shvatio ti pretpostavljas ovo [tex] [A] \subseteq [B] [/tex] i jos nesto, sto nije sad bitno :D.
Iz toga ti pokusavas dobiti [tex] x \in [A] \Rightarrow x \in [B] , \forall x [/tex]
Ali to bas znaci da je [tex] [A] \subseteq [B] [/tex]. Tak da to bas i nema smisla :D.
Neznam za ostatak, tesko je citljiv, probaj za ubuduce nauciti TeX, jer se ljudima ovak napisano neda bas citati :D. Ili ako nist drugo pisi kompletni tekst, bez kratica i "E" umjesto element i slicnih stvari, onak kak su nas ucili na elementarnoj. :D
A zasto nebi smjeli uzeti taj skup? Nismo morali bas njega uzeti, ali je on nekako najjednostavniji za dobiti kontradikciju. Jer je cijeli smisao dokaza ovaj: uzmes neki skup, dokazes da je on baza, a onda dokazes da on istovremeno nije baza, pa dobis kontradikciju. 
Added after 14 minutes:
| jema (napisa): |
Neka je lin.lj. od A podskup od lin.lj. od B te neka je x=suma svih alfa(i)*a(i), i=1,...,r. treba dokazati da je xE lin.lj. A ujedno i E lin.lj. B.
|
Ako sam ja dobro ovo shvatio ti pretpostavljas ovo [tex] [A] \subseteq [B] [/tex] i jos nesto, sto nije sad bitno  . .
Iz toga ti pokusavas dobiti [tex] x \in [A] \Rightarrow x \in [B] , \forall x [/tex]
Ali to bas znaci da je [tex] [A] \subseteq [B] [/tex]. Tak da to bas i nema smisla  . .
Neznam za ostatak, tesko je citljiv, probaj za ubuduce nauciti TeX, jer se ljudima ovak napisano neda bas citati  . Ili ako nist drugo pisi kompletni tekst, bez kratica i "E" umjesto element i slicnih stvari, onak kak su nas ucili na elementarnoj. . Ili ako nist drugo pisi kompletni tekst, bez kratica i "E" umjesto element i slicnih stvari, onak kak su nas ucili na elementarnoj. 
Zadnja promjena: gflegar; 22:51 čet, 3. 11. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
|










