| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
 Postano: 12:18 sri, 2. 5. 2007 Naslov: Postano: 12:18 sri, 2. 5. 2007 Naslov: |
    |
|
|
Krenimo redom. Gradivo (vidljivo iz naslova i podnaslova u vjezbama):
Newtonov IP, Hermiteov IP, Lagrangeov oblik IP-a, po dijelovim linearna interpolacija
Metoda bisekcije, metoda sekante, Newtonova metoda
Eulerova metoda, Runge-Kuttine metode, Impilicitno trapezna metoda
Metoda konačnih razlika za rubni problem
Iz svih ovih dijelova (izuzev Lagrangeovog oblika IP-a i metode sekante), na vjezbama je obradjen po jedan primjer ili je primjer dan za zadacu i za svaku napisanu zadacu studentu dodijeljen plus. Predanih zadaca ima 50tak (upravo onoliko koliko je studenata bilo na vjezbama). Kroz zadace se moglo provjezbati rjesavanje problema zadanom metodom.
Lagrangeov oblik IP-a razjasnjen je na zadnjim vjezbama na kojima sam dala nekoliko napomena vezanih uz kolokvij.
Za metodu sekante je dana ideja kako se rjesava - u rekurziju se ubace potrebne brojke.
Kod Runge -Kuttinih metoda ideja je slicna kao i kod Eulerove metode samo sto je funkcija koja se javlja u rekurziji nesto kompliciranija.
Na zadnjim vjezbama sam i odgovarala na nejasnoce vezane oko gradiva.
Link na zadatke s pismenih po kojima treba vjezbati dan je u nekom od ranijih postova.
Krenimo redom. Gradivo (vidljivo iz naslova i podnaslova u vjezbama):
Newtonov IP, Hermiteov IP, Lagrangeov oblik IP-a, po dijelovim linearna interpolacija
Metoda bisekcije, metoda sekante, Newtonova metoda
Eulerova metoda, Runge-Kuttine metode, Impilicitno trapezna metoda
Metoda konačnih razlika za rubni problem
Iz svih ovih dijelova (izuzev Lagrangeovog oblika IP-a i metode sekante), na vjezbama je obradjen po jedan primjer ili je primjer dan za zadacu i za svaku napisanu zadacu studentu dodijeljen plus. Predanih zadaca ima 50tak (upravo onoliko koliko je studenata bilo na vjezbama). Kroz zadace se moglo provjezbati rjesavanje problema zadanom metodom.
Lagrangeov oblik IP-a razjasnjen je na zadnjim vjezbama na kojima sam dala nekoliko napomena vezanih uz kolokvij.
Za metodu sekante je dana ideja kako se rjesava - u rekurziju se ubace potrebne brojke.
Kod Runge -Kuttinih metoda ideja je slicna kao i kod Eulerove metode samo sto je funkcija koja se javlja u rekurziji nesto kompliciranija.
Na zadnjim vjezbama sam i odgovarala na nejasnoce vezane oko gradiva.
Link na zadatke s pismenih po kojima treba vjezbati dan je u nekom od ranijih postova.
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
 Postano: 13:06 čet, 3. 5. 2007 Naslov: Postano: 13:06 čet, 3. 5. 2007 Naslov: |
    |
|
|
Slazem se...
Trazimo tocke [latex]\alpha[/latex] i [latex]\beta[/latex] takve da
1. Tangenta u ([latex]\alpha[/latex],f([latex]\alpha[/latex])) sadrzi tocku ([latex]\beta[/latex],0).
2. Tangenta u ([latex]\beta[/latex],f([latex]\beta[/latex])) sadrzi tocku ([latex]\alpha[/latex],0).
Sada imamo i gotov recept. Dakle, nadjemo te tangente i uvrstimo pripadne točke. Dobivamo sustav 2x2 i rješenje toga sustava su tražene točke [latex]\alpha[/latex] i [latex]\beta[/latex].
Slazem se...
Trazimo tocke  i i 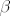 takve da takve da
1. Tangenta u ( ,f( ,f( )) sadrzi tocku ( )) sadrzi tocku (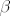 ,0). ,0).
2. Tangenta u (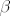 ,f( ,f(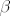 )) sadrzi tocku ( )) sadrzi tocku ( ,0). ,0).
Sada imamo i gotov recept. Dakle, nadjemo te tangente i uvrstimo pripadne točke. Dobivamo sustav 2x2 i rješenje toga sustava su tražene točke  i i 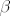 . .
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
 Postano: 6:48 pet, 4. 5. 2007 Naslov: Postano: 6:48 pet, 4. 5. 2007 Naslov: |
    |
|
|
To vam je zato što se do sada rubni problem rješavao tek u sklopu parcijalnih diferencijalnih jednadžbi (koje nam tek dolaze), a mi smo ga ove godine dotakli i u sklopu običnih diferencijalnih jednadžbi.
Probajte riješiti zadatak s vježbi s n=3, 4, 5, ... .
U većini zadataka stvarno ne može biti nekih iznenađenja, samo primijenite odgovarajući algoritam i to je to.
To vam je zato što se do sada rubni problem rješavao tek u sklopu parcijalnih diferencijalnih jednadžbi (koje nam tek dolaze), a mi smo ga ove godine dotakli i u sklopu običnih diferencijalnih jednadžbi.
Probajte riješiti zadatak s vježbi s n=3, 4, 5, ... .
U većini zadataka stvarno ne može biti nekih iznenađenja, samo primijenite odgovarajući algoritam i to je to.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
jana
Forumaš(ica)
Pridružen/a: 16. 07. 2004. (00:15:21)
Postovi: (8)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mbarberic
Forumaš(ica)


Pridružen/a: 22. 03. 2007. (19:59:25)
Postovi: (24)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|



